СТАТИЧЕСКАЯ ХАРАКТЕРИСТИКА
ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ. КАЧЕСТВО ПРОЦЕССА УПРАВЛЕНИЯ
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ КАЧЕСТВА ПО РАСПОЛОЖЕНИЮ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ В КОМПЛЕКСНОЙ ПЛОСКОСТИ
ЗАПАС УСТОЙЧИВОСТИ
ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ РАБОТЫ
Содержание задания
Содержание задания
Передаточные функции элементов структурной схемы
Передаточные функции элементов структурной схемы
Навигация
ЗАПАС УСТОЙЧИВОСТИ
Теория автоматического управления
47347
знаков
19
таблиц
22
изображения
9. ЗАПАС УСТОЙЧИВОСТИ
Запас устойчивости является мерой количественной оценки степени отстроенности параметров САУ от границы устойчивости, определяемой в соответствии с критерием Найквиста удаленностью (по модулю и фазе) годографа КЧХ (АФХ) разомкнутой системы от критической точки (-1.0; j0).
Запас устойчивости по модулю определяется величиной
DH = 1.0 - | Wp(jwо)|, (9.1)
где | Wp(jwо)| - модуль КЧХ (АЧХ) при частоте wо, соответствующей пересечению годографом Wp(jw) отрицательной полуоси вещественных величин.
Запас устойчивости по фазе соответствует углу
Dj = p- argWp(jw1), (9.2)
где - argWp(jw1) - аргумент КЧХ (АЧХ) при частоте w1, соответствующей пересечению годографом Wp(jw) окружности единичного радиуса.
Запас устойчивости может быть определен аналитически, графически по годографу КЧХ(АФХ), а также по логарифмическим АЧХ и ФЧХ.
Для аналитического определения DH следует решить относительно wо уравнение
Vp (wо)
arctg ----------------- = p
Up (wо)
и подставить найденное wо в (9.1).
Аналогично, для определения Dj необходимо из уравнения
ÖU2p (w1) + V2p(w1) = 1.0
найти значение w1 и подставить его в (9.2).
Графическое определение DН и Dj по КЧХ не нуждается в пояснениях. Следует только иметь в виду, что для определения Dj непосредственно из графика должны быть приняты одинаковыми масштабы по осям координат комплексной плоскости.
Для определения запасов устойчивости по логарифмическим частотным характеристикам следует рассмотреть интервал частот, для которого L(w) > 0. На этом интервале значение DL(wо), соответствующее частоте wо, при которой j(wо) = - p(-3p, -5p, ...) определяет запас по модулю (в децибелах). Аналогично, значение j(w1), соответствующее частоте w1, при которой L(w1) = 0, дает запас устойчивости по фазе.
В качестве примера на рис.9.1. приведен годограф КЧХ разомкнутой САУ рис.3.1 Годограф не пересекает полуось отрицательных вещественных величин, поэтому DH = 1.0. Запас устойчивости по фазе Dj = 70° определен по пересечению годографа с окружностью единичного радиуса. Полученные значения DH и Dj свидетельствуют о достаточно высоком запасе устойчивости замкнутой САУ рис.3.1.
| U(w) | 8.68 | 2.5 | 0.7 | 0.28 | 0.04 | -0.09 | -0.15 | -0.17 | 0 |
| V(w) | -2.86 | -4.4 | -2.9 | -2.18 | -1.6 | -1.15 | -0.8 | -0.56 | 0 |
| w,рад/с | 0.001 | 0.005 | 0.009 | 0.013 | 0.018 | 0.025 | 0.035 | 0.05 | ¥ |
Рис.9.1. КЧХ разомкнутой САУ рис.3.1 при Ку = 20, Кос = 20.
Похожие работы
... Вид характеристики зависит от свойств самого регулятора, характеристик ИО и ОР. Вопросы устойчивости, характеризующейся динамическими свойствами АСР, являются основными при изучении теории и эксплуатации средств автоматического регулирования. Определение температуры является одним из сложных и трудоемких процессов измерения, основанным на теплообмене между телами. Приборы, входящие в тепловой ...
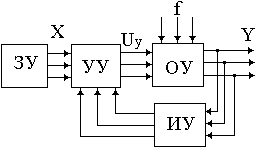
... поведение регулируемой величины. Управляющее воздействие вырабатывается устройством управления (УУ). Совокупность взаимодействующих управляющего устройства и управляемого объекта образует систему автоматического управления. Система автоматического управления (САУ) поддерживает или улучшает функционирование управляемого объекта. В ряде случаев вспомогательные для САУ операции (пуск, остановка, ...
... значениях функции. Начальное значение функции:. (2.10) Конечное значение функции: . (2.11) 7. Теорема запаздывания . (2.12) 4. Дифференциальные уравнения САУ При математическом описании систем автоматического управления составляют уравнения статики и динамики. Уравнения статики описывают установившиеся режимы и, как правило, являются алгебраическими. Уравнения динамики ...
... можно судить, если в пространстве изменяемых параметров построить область устойчивости, т.е. выделить область значений параметров, при которых система сохраняет устойчивость. Область устойчивости в теории автоматического управления принято называть D – областью, а представление области параметров в виде областей устойчивости и неустойчивости называют D – разбиением. Построение области ...
0 комментариев