Проверим реализуемость тактограммы
Составляем формулы включений и произведём их упрощение
Построим схему управления на пневматических элементах
Определение цикла работы механизма
Определение сил давления газа для 12 положений каждого из поршней
Построение планов скоростей для каждого из 12 положений механизма
Вычисление приведённого момента движущих сил
Определение момента инерции маховика
Сила инерции шатуна, направленная из точки S2 (центр масс шатуна) в противоположную сторону ускорения точки S2
Навигация
Построение планов скоростей для каждого из 12 положений механизма
Динамический синтез и анализ рычажного механизма
25692
знака
11
таблиц
2
изображения
2.5 Построение планов скоростей для каждого из 12 положений механизма
Для построения плана скоростей используем векторные равенства и свойства планов.
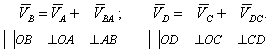
Определяем угловую скорость кривошипа:
рад/с
Определяем скорости точек А и С:
м/с
Для построения плана скоростей произвольно выбираем полюс р и выбираем длину вектора ра, соответствующую скорости точки А. Допустим ра =40 мм.
Тогда масштабный коэффициент планов скоростей равен:
м/с*мм
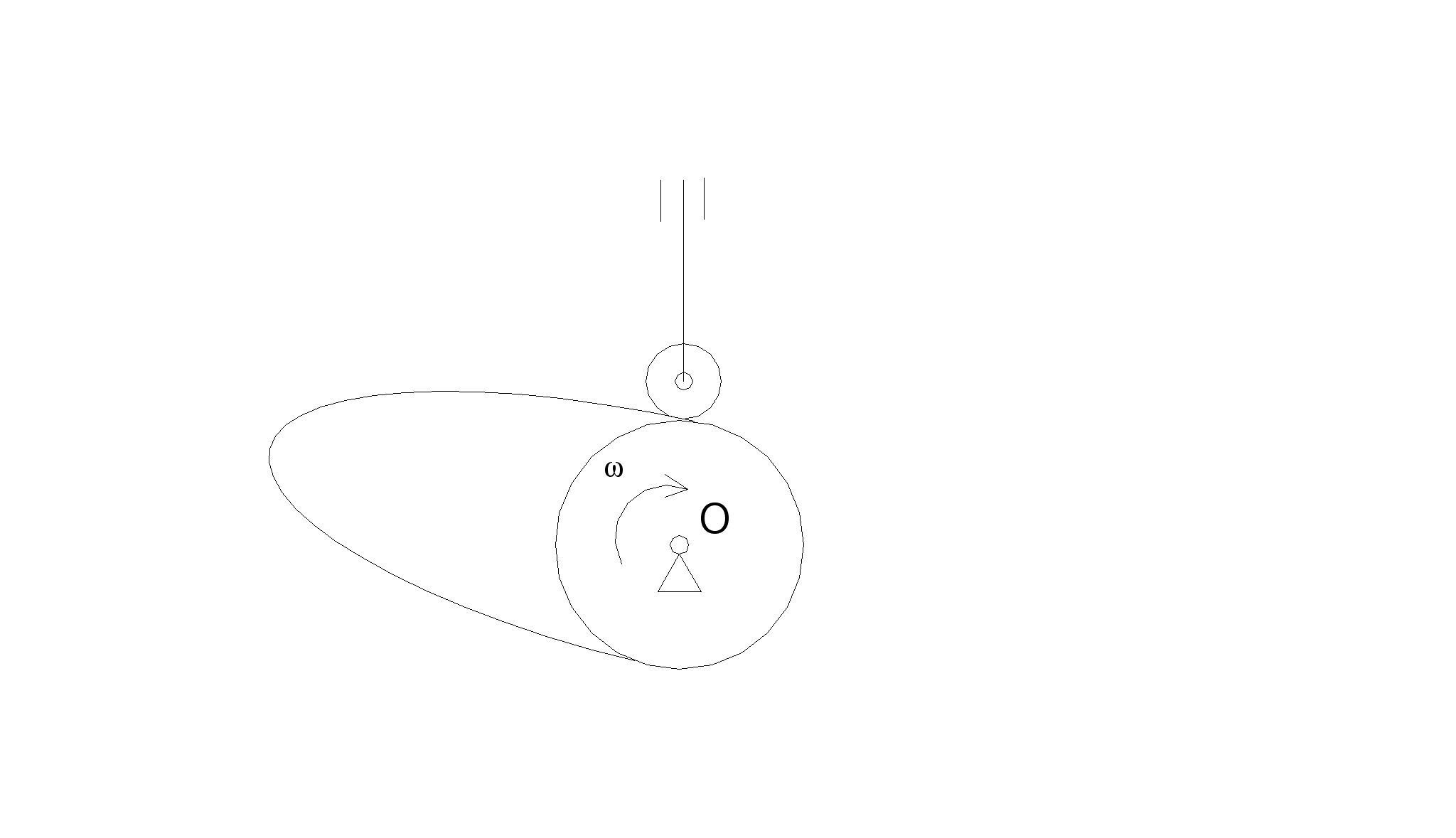
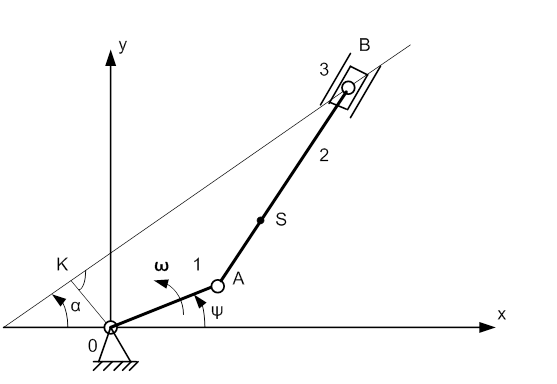
а)Проводим линию ра (из полюса р) по направлению скорости точки А (перпендикулярно ОА). Отмечаем точку а и изображаем вектор ра (от полюса р к точке а).
б)Из точки р проводим линию параллельную ОВ, т.е. линию параллельную движению поршня.
в) Через точку а проводим линию, перпендикулярную линии АВ до пересечения с линией проведённой в пункте б. Точку пересечения обозначаем буквой b. Тогда вектор ab соответствует скорости звена АВ (шатуна), а вектор рb - скорости точки В (поршня). Если на отрезке аb изобразить точку S2, причём, aS2=1/3ab тогда вектор pS2 соответствует скорости движения центра масс звена АВ в точке S2.
Так же строится план скоростей для движения звена СD и точки D.
После построения 12 планов скоростей для каждого из 12 положений механизма можно определить скорости точек В и D. Для этого, величину отрезков рb и рd следует умножить на масштабный коэффициент.
2.6 Вычисление приведённого момента инерции механизма
За звено приведения принимаем входное звено (кривошип АВ).
Для каждого положения механизма приведённый момент инерции звеньев находится по формуле
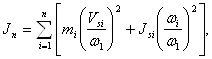
где 
-масса звена i; 
-момент инерции звена i относительно оси, проходящей через центр масс 
звена; 
-угловая скорость звена i; 
-скорость центра масс звена i.
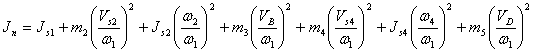
Учитывая, что 
,
получаем:
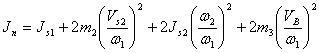
Рассмотрим формулу по частям:
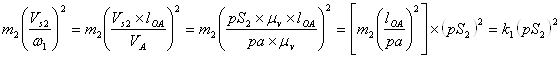
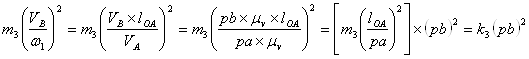
Так как в квадратных скобках величины постоянные не зависимые от положения механизма их можно сразу высчитать.
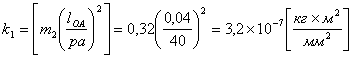
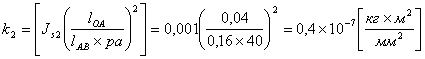
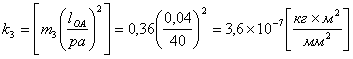
Конечная формула для вычисления приведённого момента инерции будет иметь вид:
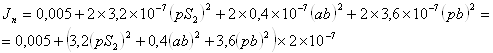
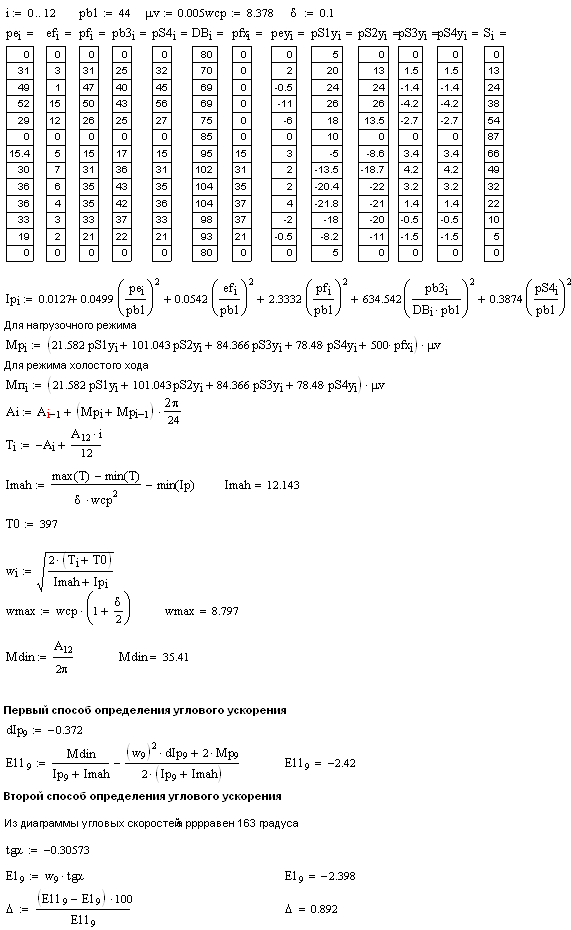
Вычислим приведённые моменты инерции для 12 положений механизма и результаты занесем в таблицу.
Таблица 2.7. Приведённые моменты инерции 12 положений механизма.
| № п/п | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|
| 27 | 32 | 38 | 40 | 36 | 30 | 27 | 30 | 36 | 40 | 38 | 32 |
| ab [мм] | 40 | 35 | 21 | 0 | 21 | 35 | 40 | 35 | 21 | 0 | 21 | 35 |
| pb [мм] | 0 | 24 | 39 | 40 | 30 | 17 | 0 | 17 | 30 | 40 | 39 | 24 |
|
| 5594 | 6168 | 7055 | 7176 | 6513 | 5882 | 5594 | 5882 | 6513 | 7176 | 7055 | 6168 |
[мм]
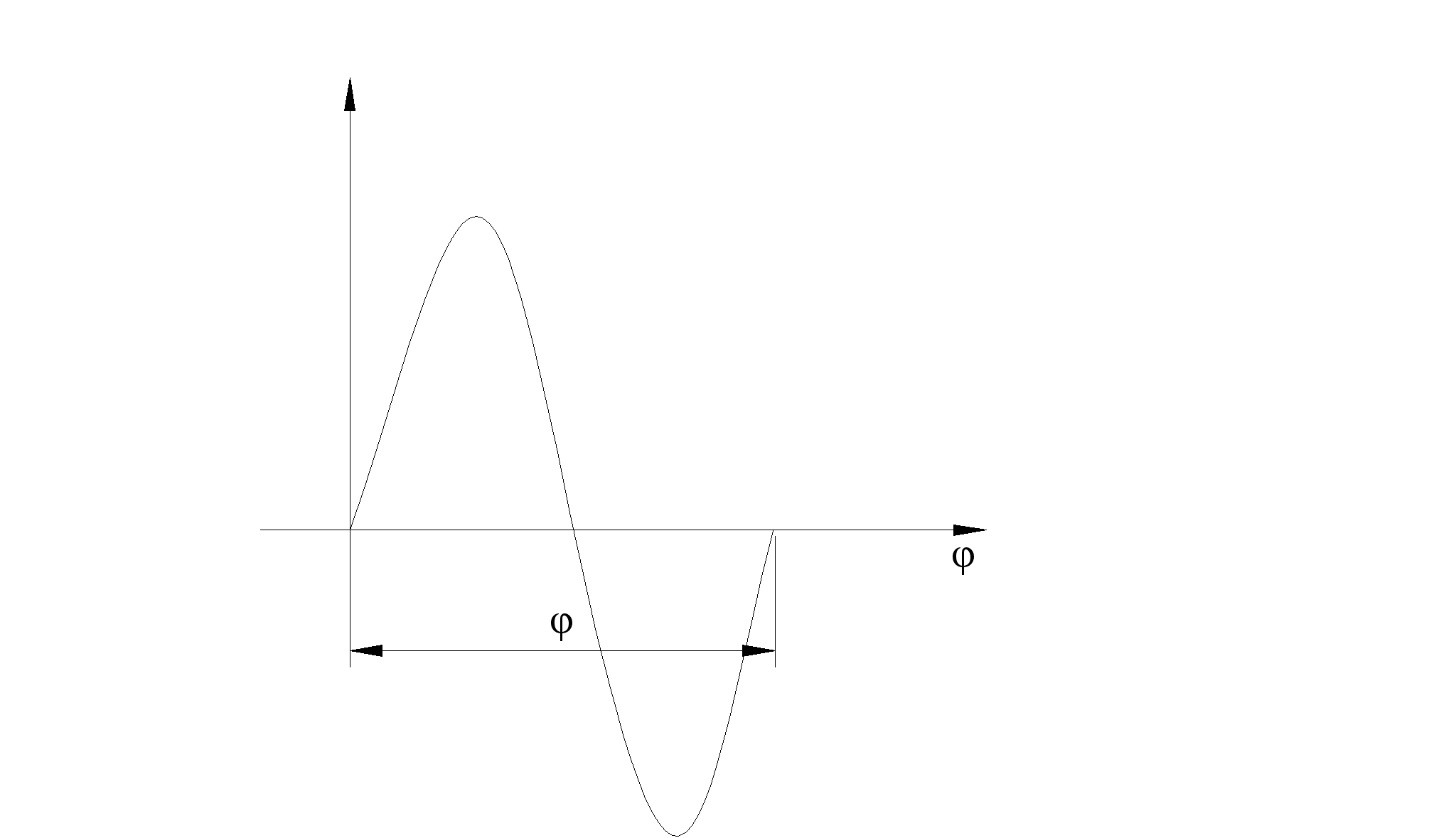
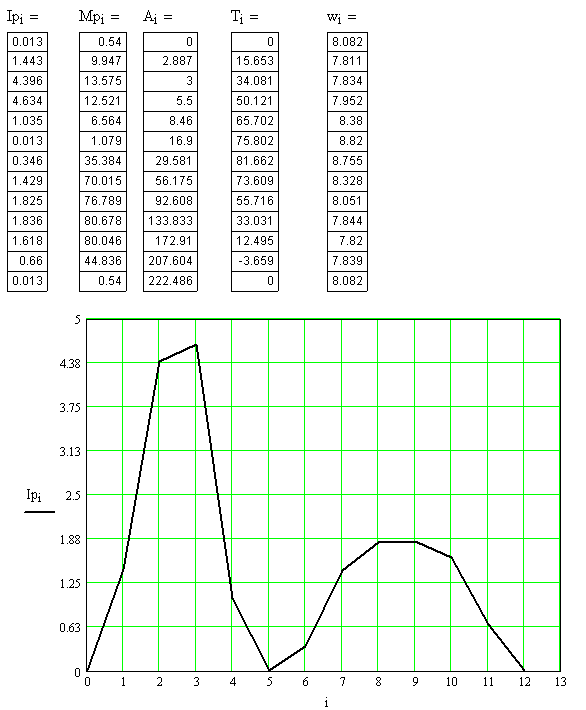
По полученным 12 значениям строим диаграмму приведённого момента инерции, при этом ось абсцисс расположим вертикально.
Выбираем масштабный коэффициент
Похожие работы
... механизма для обеспечения эффективного перехода на различные способы транспортирования в зависимости от свойств материала и выполняемой технологической операции. Разработке методов кинематического анализа механизмов транспортирования ткани швейных машин и соответствующего этой задаче алгоритмического и программного обеспечения посвящены работы. [67],[71],[72]. В работе Ю.Ю.Щербаня и В.А.Горобца ...
... B[44] = 220.000 TETA[44] = 0.0 R[45] = 52.000 B[45] = 220.000 TETA[45] = 0.0 R[46] = 52.000 B[46] = 360.000 TETA[46] = 0.0 6. Силовое исследование рычажного механизма. 6.1 Задачи силового исследования. При силовом исследовании решаются следующие задачи Определение сил действующих на звенья механизма. Определение реакций в кинематических ...
... 8-Планетарный механизм Исходные данные: n1=1570об/мин; n5=140об/мин; m=4мм; z4=15; z5=26. В данной задаче необходимо определить число зубьев 1,2,3 планетарной ступени механизма. Подобрать число сателлитов. 2.1.2 Определяем число зубьев планетарной ступени (1) (2) (3) (4) 2.1.3 Условие соосности (5) (6) Подставляем выражение (6) в передаточное отношение первого ...
... : Массы звеньев: Моменты инерции звеньев: После подстановки значений рассчитанных величин получим следующую формулу: 2.4.4 Расчет приведенных моментов сил На входное звено крышкоделательной машины при рабочем ходе действует сила полезного сопротивления P n.с.=500 H. Величину приведенного момента сил сопротивления определяем по формуле: Определим ...
0 комментариев