Навигация
1.1 Метод дихотомии
В этом методе точки x1 и х2 располагаются близко к середине очередного отрезка [а; b], т.е:
, (2.11)
где d > 0 – малое число. При этом отношение длин нового и исходного отрезков
близко к 1/2, этим и объясняется название метода.
Отметим, что для любых точек x1 и х2 величина t > 1/2, поэтому указанный выбор пробных точек объясняется стремлением обеспечить максимально возможное относительное уменьшение отрезка на каждой итерации поиска х*.
В конце вычислений по методу дихотомии в качестве приближенного значения х* берут середину последнего из найденных отрезков [а; b], убедившись предварительно, что достигнуто неравенство
.
Опишем алгоритм метода деления отрезка пополам.
Шаг 1. Определить x1 и х2 по формулам (2.11). Вычислить f (x1) и f (x2).
Шаг 2. Сравнить f (x1) и f (x2). Если 
, то перейти к отрезку [а; x2], положив b = x2 , иначе – к отрезку [x1; b], положив а = x1 .
Шаг 3. Найти достигнутую точность
Если 
, то перейти к следующей итерации, вернувшись к шагу 1. Если 
, то завершить поиск х*, перейдя к шагу 4.
Шаг 4. Положить
.
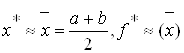Замечания:
1. Число d из (2.11) выбирают на интервале (0;2e) с учетом следующих соображений:
а) чем меньше d, тем больше относительное уменьшение длины отрезка на каждой итерации, т.е. при уменьшении d достигается более высокая скорость сходимости метода дихотомии;
б) при чрезмерно малом d сравнение значений f (x) в точках x1 и х2 , отличающихся на величину d, становится затруднительным. Поэтому выбор d должен быть согласован с точностью определения f (x) и с количеством верных десятичных знаков при задании аргумента х.
В таблице 1 приведено решение задания по варианту.
Таблица 1 - Метод дихотомии
| № шага | x1 | x2 | F(x1) | F(x2) | а | b |
|
| 1 | 3.29 | 3.31 | --3.3662671 | -3.3081836 | 2.7 | 3.9 | 0.6 |
| 2 | 2.995 | 3.0015 | -3.9477432 | -3.9985552 | 2.7 | 3.301 | 0.3 |
| 3 | 3.1425 | 3.1525 | -5.7966545 | -5.7920936 | 2.995 | 3.301 | 0.15075 |
| 4 | 2.9995 | 3.15125 | -5.3956845 | -5.4206115 | 3.06875 | 3.1625 | 0.04687 |
| 5 | 3.1118125 | 3.1138125 | -5.7344664 | -5.7448499 | 3.074375 | 3.15125 | 0.03844 |
| 6 | 3.1305312 | 3.1325312 | -5.8005444 | -5.8034734 | 3.1118125 | 3.15125 | 0.01972 |
| 7 | 3.1398906 | 3.1418906 | -5.8073633 | -5.8065477 | 3.1305312 | 3.15125 | 0.01036 |
| 8 | 3.1352109 | 3.1372109 | -5.8061441 | -5.8072013 | 3.1305312 | 3.1418906 | 5.67969E-3 |
| 9 | 3.1309766 | 3.1509766 | -5.8073015 | -5.8074223 | 3.1352109 | 3.1418906 | 3.33984E-3 |
| 10 | 3.1387207 | 3.1407207 | -5.8074693 | -5.807122 | 3.1375508 | 3.1465703 | 2.16992E-3 |
| 11 | 3.1381357 | 3.1401357 | -5.8074196 | -5.8073064 | 3.1375508 | 3.1407207 | 1.585E-3 |
| 12 | 3.1384282 | 3.1404282 | -5.807453 | -5.8072227 | 3.1381357 | 3.1407207 | 1.292E-3 |
|a-b|=0.001<= ε, x*=(a+b)/2=3.139282, f(x*)=-5.8074527
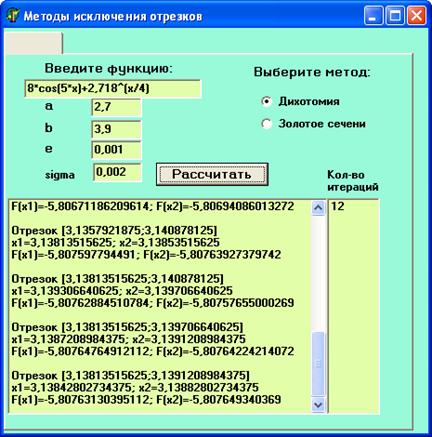
Рисунок 1 – Результат выполнения программы (Метод дихотомии).
Похожие работы
... МП к некритическому экстраполированию результата считается его слабостью. Сети РБФ более чувствительны к «проклятию размерности» и испытывают значительные трудности, когда число входов велико. 5. МОДЕЛИРОВАНИЕ НЕЙРОННЫХ СЕТЕЙ ДЛЯ ПРОГНОЗИРОВАНИЯ СТОИМОСТИ НЕДВИЖИМОСТИ 5.1 Особенности нейросетевого прогнозирования в задаче оценки стоимости недвижимости Использование нейронных сетей можно ...
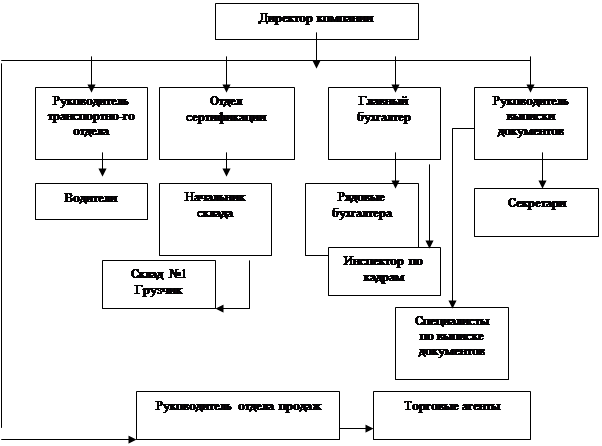
... с издержками двух или трех конкурентов. Это позволит выявить конкурентоспособность предприятия, определить имеющиеся резервы для снижения издержек. Подобный сравнительный анализ издержек производства на данном предприятии и предприятиях-конкурентах служит основанием для разработки и проведения стратегических мероприятий по снижению издержек производства и оптимизации производственной программы. ...
... от года-x и от номера месяца в году-y следующим образом: F(x)=50-x2+10x-y2+10y. Определите, в каком году и в каком месяце прибыль была максимальной. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МЕТОДЫ ОПТИМИЗАЦИИ Билет № 22 1) Постановка вариационной задачи с ограничениями. Привести пример. 2) Дайте геометрическую ...
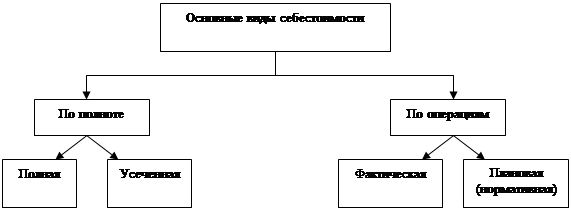
... ) аппарат, а затем полученную величину корректируют с учетом других факторов (долгосрочная стратегия предприятия, ограничения по производственным мощностям и пр). 3. Рекомендации по оптимизации величины себестоимости продукции на основе анализа соотношения "затраты - объем - прибыль" 3.1 Деление затрат на постоянные и переменные части и определение показателей маржинального дохода ...
0 комментариев