Навигация
Метод деформированного симплекса
2.4 Метод деформированного симплекса
Алгоритм минимизации по правильному симплексу можно модифицировать, добавив к процедуре отражения при построении нового симплекса процедуры сжатия и растяжения. А именно, положение новой вершины y вместо вершины xn , соответствующей наибольшему значению функции, находится сравнением и выбором наименьшего среди значений целевой функции в точках:
z1= xc - a( xc - xn), 0<a<1;
z2 = xc + a( xc - xn), 0<a<1;
z3 = xc + b( xc - xn), b приближенно равно 1;
z4 = xc + g( xc - xn), g<1.
Геометрическая иллюстрация этих процедур для двумерного пространства приведена на рисунке 7.
Новые симплексы полученные в результате процедуры сжатия (a,b); отражения (c); растяжения (d)
Так как величина a принадлежит интервалу (0;1), то выбор точек z1 и z2 соответствует сжатию симплекса; b приближенно равно 1, поэтому выбор точки z3 соответствует отражению, а g>1 и выбор точки z4 приводит к растяжению симплекса.
Отметим, что при деформациях утрачивается свойство правильности исходного симплекса.
Алгоритм метода поиска точки минимума функции по деформируемому симплексу
Начальный этап. Выбрать параметр точности eps, параметры a, b и g, базовую точку x0 , параметр a и построить начальный симплекс. Вычислить значение функции f(x0).
Основной этап. Шаг 1. Вычислить значения функции в вершинах симплекса x1,..., xn.
Шаг 2. Упорядочить вершины симплекса x0,..., xn так, чтобы f(x0)<=f(x1)<=...<=f(x[n-1])<=f(xn).
Шаг 3. Проверить условие (1/n)Sum[f(xi)-f(x0)]^2 < e^2, i=[1,n].
Это одно из возможных условий останова. При его выполнении "дисперсия" значений f(x) в вершинах симплекса становится меньше e2, что, как правило, соответствует либо малому ребру a симплекса, либо попаданию точки минимума x* внутрь симплекса, либо тому и другому одновременно.Если это условие выполнено, то вычисления прекратить, полагая x*= x0. В противном случае перейти к шагу 4.
Шаг 4. Найти xс и пробные точки zk , k=1,...,4 по формулам (2). Найти f(z*)=minf(zk). Если f(z*)<f(xn), то положить xn = z* и перейти к шагу 2. Иначе - перейти к шагу 5.
Шаг 5. Уменьшить симплекс, полагая xi=( xi+ x0)/2, i=1,...,n перейти к шагу 1.
На практике хорошо зарекомендовал себя следующий набор параметров a=1/2, b=1, g=2, поэтому он и был использован в программе.
Таблица 5 – Метод деформированного симплекса
| № шага | Z(x0,y0) | Z(x1,y1) | Z(x2,y2) |
| 1 | 5,25127562399313 | 5,35273629457997 | 4,72465845389651 |
| 2 | 4,47048359472409 | 5,52371793491734 | 4,32427361628427 |
| 3 | 4,26941489330181 | 4,56183485018145 | 2,53610076197985 |
| 4 | 2,53610076197985 | 4,26941489330181 | 2,54614140634749 |
| 5 | 2,60406550474582 | 2,62414679348111 | 0,650136727095332 |
| 6 | 0,873172338270091 | 4,78102989357106 | -0,460995375774572 |
| 7 | -0,460995375774572 | -0,183165198484471 | -0,647802169588968 |
| 8 | -0,647802169588968 | -0,460995375774572 | -0,752046189909185 |
| 9 | -0,752046189909185 | -0,647802169588968 | -0,743774186218157 |
| 10 | -0,824978188986428 | -0,820842187140914 | -0,807869388437316 |
| 11 | -0,848148148136976 | -0,848148148106495 | -0,848148148103467 |
| 12 | -0,848148148146818 | -0,848148148131578 | -0,848148148135116 |
| 13 | -0,848148148146818 | -0,848148148135116 | -0,848148148139001 |
| 14 | -0,848148148136976 | -0,848148148106495 | -0,848148148103467 |
| 15 | -0,848148148148147 | -0,848148148148145 | -0,848148148148146 |
| 16 | -0,848148148148148 | -0,848148148148147 | -0,848148148148147 |
T.к.
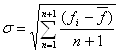 < ε,
< ε,
то примем x=0,237037034153931 и y=0,407407409218273 Z(x,y)= -0,848148148148148
Сравнив все методы, мы видим, что для данной функции лучше подходит метод деформированного симплекса, т.к. он быстрее приводит к оптимальному решению.
Похожие работы
... МП к некритическому экстраполированию результата считается его слабостью. Сети РБФ более чувствительны к «проклятию размерности» и испытывают значительные трудности, когда число входов велико. 5. МОДЕЛИРОВАНИЕ НЕЙРОННЫХ СЕТЕЙ ДЛЯ ПРОГНОЗИРОВАНИЯ СТОИМОСТИ НЕДВИЖИМОСТИ 5.1 Особенности нейросетевого прогнозирования в задаче оценки стоимости недвижимости Использование нейронных сетей можно ...
... с издержками двух или трех конкурентов. Это позволит выявить конкурентоспособность предприятия, определить имеющиеся резервы для снижения издержек. Подобный сравнительный анализ издержек производства на данном предприятии и предприятиях-конкурентах служит основанием для разработки и проведения стратегических мероприятий по снижению издержек производства и оптимизации производственной программы. ...
... от года-x и от номера месяца в году-y следующим образом: F(x)=50-x2+10x-y2+10y. Определите, в каком году и в каком месяце прибыль была максимальной. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МЕТОДЫ ОПТИМИЗАЦИИ Билет № 22 1) Постановка вариационной задачи с ограничениями. Привести пример. 2) Дайте геометрическую ...
... ) аппарат, а затем полученную величину корректируют с учетом других факторов (долгосрочная стратегия предприятия, ограничения по производственным мощностям и пр). 3. Рекомендации по оптимизации величины себестоимости продукции на основе анализа соотношения "затраты - объем - прибыль" 3.1 Деление затрат на постоянные и переменные части и определение показателей маржинального дохода ...

0 комментариев