Метод Хука – Дживса

2.2 Метод Хука – Дживса

Метод Хука и Дживса осуществляет два типа поиска - исследующий поиск и поиск по образцу. Первые две итерации процедуры показаны на рисунке 4.

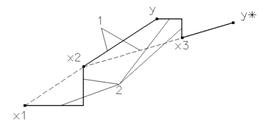
Рисунок 4 – 1-поиск по образцу; 2- исследующий поиск вдоль координатных осей.

При заданном начальном векторе x1 исследующий поиск по координатным направлениям приводит в точку x2 . Последующий поиск по образцу в направлении x1- x2 приводит в точку y. Затем исследующий поиск, начинающийся из точки y, дает точку x3. Следующий этап поиска по образцу вдоль направления x3- x2 дает y*. Затем процесс повторяется.

Рассмотрим вариант метода, использующий одномерную минимизацию вдоль координатных направлений d1,..., dn и направлений поиска по образцу.

Начальный этап. Выбрать число eps > 0 для остановки алгоритма. Выбрать начальную точку x1, положить y1= x1, k=j=1 и перейти к основному этапу.

Основной этап.

Шаг 1. Вычилить lymj - оптимальное решение задачи минимизации f(yj+lym * dj) при условии lym принадлежит E1. Положить y[j+1]= yj+lymj*dj. Если j < n, то заменить j на j+1 и вернуться к шагу 1. Если j=n, то положить x[k+1] = y[n+1]. Если ||x[k+1] - xk|| < eps , то остановиться; в противном случае перейти к шагу 2.

Шаг 2. Положить d = x[k+1] - xk и найти lym - оптимальное решение задачи минимизации f(x[k+1]+lym*d) при условии lym принадлежит E1. Положить y1= x[k+1]+lym*d, j=1, заменить k на k+1 и перейти к шагу 1. Для решения поставленной задачи выбрано приближение ε=0,02, α=0,15

Таблица 4 - Метод Хука-Дживса

Т.к в ε окрестности полученной на 38 шаге точке мы не получаем улучшения (уменьшения значения) функции, то примем x1=0,426999999999999 x2=0,496999999999999,

Z(x1,x2)= -0,699011600000001.

Похожие работы

Анализ методов прогнозирования и моделирование нейронных сетей для прогнозирования стоимости недвижимости

Скачать

110516

5

18

... МП к некритическому экстраполированию результата считается его слабостью. Сети РБФ более чувствительны к «проклятию размерности» и испытывают значительные трудности, когда число входов велико. 5. МОДЕЛИРОВАНИЕ НЕЙРОННЫХ СЕТЕЙ ДЛЯ ПРОГНОЗИРОВАНИЯ СТОИМОСТИ НЕДВИЖИМОСТИ   5.1 Особенности нейросетевого прогнозирования в задаче оценки стоимости недвижимости Использование нейронных сетей можно ...

Сравнительный анализ определения кредитоспособности предприятия-заемщика

Скачать

161484

23

0

... с издержками двух или трех конкурентов. Это позволит выявить конкурентоспособность предприятия, определить имеющиеся резервы для снижения издержек. Подобный сравнительный анализ издержек производства на данном предприятии и предприятиях-конкурентах служит основанием для разработки и проведения стратегических мероприятий по снижению издержек производства и оптимизации производственной программы. ...

Экзаменационные билеты по методам оптимизации за весенний семестр 2001 года

Скачать

41899

0

0

... от года-x и от номера месяца в году-y следующим образом: F(x)=50-x2+10x-y2+10y. Определите, в каком году и в каком месяце прибыль была максимальной. Зав. кафедрой --------------------------------------------------   Экзаменационный билет по предмету МЕТОДЫ ОПТИМИЗАЦИИ Билет № 22 1) Постановка вариационной задачи с ограничениями. Привести пример. 2) Дайте геометрическую ...

Использование приемов операционного анализа в оптимизации величины себестоимости продукции

Скачать

137570

20

2

... ) аппарат, а затем полученную величину корректируют с учетом других факторов (долгосрочная стратегия предприятия, ограничения по производственным мощностям и пр). 3. Рекомендации по оптимизации величины себестоимости продукции на основе анализа соотношения "затраты - объем - прибыль" 3.1 Деление затрат на постоянные и переменные части и определение показателей маржинального дохода ...