Навигация
1.2 Метод золотого сечения
Метод золотого сечения. Рассмотрим такое симметричное расположение точек x1 и х2 на отрезке [а; b], при котором одна из них становится пробной точкой и на новом отрезке, полученном после исключения части исходного отрезка. Использование таких точек позволяет на каждой итерации метода исключения отрезков, кроме первой, ограничиться определением только одного значения f (x), так как другое значение уже найдено на одной из предыдущих итераций.
Найдем точки x1 и х2 , обладающие указанным свойством.
Рассмотрим сначала отрезок [0; 1] и для определенности предположим, что при его уменьшении исключается правая часть этого отрезка. Пусть х2 = t, тогда симметрично расположенная точка х1 = 1–t (рис. 2.7).
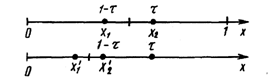
Рис. 2.7. Определение пробных точек в методе золотого сечения
Пробная точка х1 отрезка [0; 1] перейдет в пробную точку х2¢ = 1–t нового отрезка [0; т]. Чтобы точки х2 = t, и х2¢ = 1–t делили отрезки [0; 1] и [0; t] в одном и том же отношении, должно выполняться равенство
![]()
или
![]() ,
,
откуда находим положительное значение
![]() …
…
Таким образом,
х1 = 1–t = ![]() ,
, ![]() .
.
Для произвольного отрезка [а; b] выражения для пробных точек примут вид
![]() ;
;
![]()
В таблице 2 приведено решение задания по варианту.
Опишем алгоритм метода золотого сечения.
Шаг 1. Найти х1 и х2 по формулам (2.15). Вычислить f (x1) и f (x2). Положить ![]() ,
,
![]() .
.
Шаг 2. Проверка на окончание поиска: если en > e, то перейти к шагу 3, иначе – к шагу 4.
Шаг 3. Переход к новому отрезку и новым пробным точкам. Если f (x1) £ f (x2) то положить b=x2 , x2=x1 , f (x2) £ f (x1), x1=b–t(b–a) и вычислить f (x1), иначе – положить a=x1, x1= x2 , f (x1) = f (x2), x2=b+t(b–a) и вычислить f (x2). Положить en = ten и перейти к шагу 2.
Шаг 4. Окончание поиска: положить
![]() ,
, ![]() .
.
Результаты вычислений на остальных итерациях представлены в таблице 2 .
Таблица 2 - Метод золотого сечения
| № шага | a | b | x1 | x2 | F(x1) | F(x2) |
|
| 1 | 2.7 | 3.9 | 3.1584 | 3.4416 | -5.7694 | 1.79829 | 0.370820393 |
| 2 | 2.7 | 3.4416 | 2.98329 | 3.1583 | -3.1542 | -5.7698 | 0.229179607 |
| 3 | 2.9833 | 3.4416 | 3.158365 | 3.26652 | -5.76957 | -4.22659 | |
| 4 | 2.98329 | 3.266546 | 3.09148 | 3.15833 | -5.58444 | -5.769704 | |
| 5 | 3.09148 | 3.26652 | 3.15835 | 3.199661 | -5.76962 | -5.43999 | |
| 6 | 3.09148 | 3.19966 | 3.13281 | 3.15834 | -5.8039 | -5.76967 | |
| 7 | 3.09148 | 3.15834 | 3.11702 | 3.132801 | -5.7600 | -580399 | |
| 8 | 3.11702 | 3.15834 | 3.13281 | 3.14256 | -5.8039 | -5.80627 | |
| 9 | 3.13281 | 3.15834 | 3.14256 | 3.14859 | -5.8063 | -5.7982 | |
| 10 | 3.13281 | 3.14859 | 3.1388 | 3.14856 | -5.08076 | -5.8063 | |
| 11 | 3.13281 | 3.14256 | 3.13653 | 3.13883 | -5.8071 | -5.8076 | |
| 12 | 3.13653 | 3.142557 | 3.13883 | 3.140255 | -5.80764 | -5.80745 | |
| 13 |
|a-b|=7.893370498E-3< ε, x*=(a+b)/2=3.1407091
f(x*)=-5.807126299
Сравнив два метода, мы видим, что для данной функции лучше подходит метод дихотомии, т.к. он быстрее приводит к оптимальному решению.
Похожие работы
... МП к некритическому экстраполированию результата считается его слабостью. Сети РБФ более чувствительны к «проклятию размерности» и испытывают значительные трудности, когда число входов велико. 5. МОДЕЛИРОВАНИЕ НЕЙРОННЫХ СЕТЕЙ ДЛЯ ПРОГНОЗИРОВАНИЯ СТОИМОСТИ НЕДВИЖИМОСТИ 5.1 Особенности нейросетевого прогнозирования в задаче оценки стоимости недвижимости Использование нейронных сетей можно ...
... с издержками двух или трех конкурентов. Это позволит выявить конкурентоспособность предприятия, определить имеющиеся резервы для снижения издержек. Подобный сравнительный анализ издержек производства на данном предприятии и предприятиях-конкурентах служит основанием для разработки и проведения стратегических мероприятий по снижению издержек производства и оптимизации производственной программы. ...
... от года-x и от номера месяца в году-y следующим образом: F(x)=50-x2+10x-y2+10y. Определите, в каком году и в каком месяце прибыль была максимальной. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МЕТОДЫ ОПТИМИЗАЦИИ Билет № 22 1) Постановка вариационной задачи с ограничениями. Привести пример. 2) Дайте геометрическую ...
... ) аппарат, а затем полученную величину корректируют с учетом других факторов (долгосрочная стратегия предприятия, ограничения по производственным мощностям и пр). 3. Рекомендации по оптимизации величины себестоимости продукции на основе анализа соотношения "затраты - объем - прибыль" 3.1 Деление затрат на постоянные и переменные части и определение показателей маржинального дохода ...

0 комментариев