Навигация
Метод правильного симплекса
2.3 Метод правильного симплекса
Правильный симплекс в пространстве En называется множество из n+1 равноудаленных друг от друга точек (вершин симплекса). В пространстве Е2 правильным симплексом является совокупность вершин равностороннего треугольника, Е3 – правильного тетраэдра.
Поиск точки минимума функции f(x) с помощью правильных симплексов производят следующим образом. На каждой итерации сравниваются значения f(x) в вершинах симплекса. Затем проводят описанную выше процедуру отражения для этой вершины, в которой f(x) принимает наибольшее значение. Если в отраженной вершине получается меньшее значение функции, то переходят к новому симплексу. В противном случае выполняют еще одну попытку отражения для вершины со следующим по величине значением f(x). Если и она не приводит к уменьшению функции, то сокращают длину ребра симплекса и строят новый симплекс с новым ребром. В качестве базовой выбирают ту вершину х0 старого симплекса, которой функция принимает наименьшее значение. Поиск минимума f(x) заканчивают, когда либо ребро симплекса, либо разность между значениями функции в вершинах симплекса становятся достаточно малыми.
Начальный этап. Выбрать параметр точности eps, базовую точку x0, ребро a и построить начальный симплекс. Вычислить f(x0).
Основной этап.
Шаг 1. Вычислить значения f(x) в вершинах симплекса x1,..., xn.
Шаг 2. Упорядочить вершины симплекса x0,..., xn так, чтобы f(x0)<=f(x1)<=...<=f(x[n-1])<=f(xn).
Шаг 3. Проверим на окончание поиска
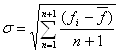 ,
,
где

Это одно из возможных условий останова. Его выполнении соответствует либо малому ребру a симплекса, либо попаданию точки минимума x* внутрь симплекса, либо тому и другому одновременно.
Если это условие выполнено, то вычисления прекратить, полагая x*= x0. В противном случае перейти к шагу 4.
Шаг 4. Найти xс и выполнить отражение вершины xn : y=2*xс- xn. Если f(y)<f(xn), то положить xn=y и перейти к шагу 2. Иначе - перейти к шагу 5.
Шаг 5. Перейти к новому правильному симплексу с вдвое меньшим ребром, считая базовой вершиной x0. Остальные n вершин симплекса найти по формуле xi=( xi+ x0)/2, i=1,...,n. Перейти к шагу 1.
Для решения поставленной задачи выбрано приближение ε=0,01, α=0,3
Таблица 5 - Метод симплекса
| № шага | Z(x0,y0) | Z(x1,y1) | Z(x2,y2) | α |
| 1 | 5,2755004 | 7,4172004 | 5,62549807735416 | 0,3 |
| 2 | 5,2755004 | 5,62549807735416 | 3,76366398915256 | 0,3 |
| 3 | 3,76366398915256 | 5,2755004 | 3,5838004 | 0,3 |
| 4 | 3,5838004 | 3,76366398915256 | 2,35182990095096 | 0,3 |
| 5 | 2,35182990095096 | 3,5838004 | 2,3421004 | 0,3 |
| 6 | 2,3421004 | 2,35182990095096 | 1,38999581274936 | 0,3 |
| 7 | 1,38999581274936 | 2,3421004 | 1,5504004 | 0,3 |
| 8 | 1,38999581274936 | 1,5504004 | 0,878161724547756 | 0,3 |
| 9 | 0,878161724547756 | 1,38999581274936 | 0,657100646520204 | 0,3 |
| 10 | 0,657100646520204 | 0,878161724547756 | 0,425132470117002 | 0,3 |
| 11 | 0,425132470117002 | 0,657100646520204 | 0,143414901312537 | 0,3 |
| 12 | 0,143414901312537 | 0,425132470117002 | 0,191312636707734 | 0,3 |
| 13 | 0,143414901312537 | 0,191312636707734 | -0,15106142287364 | 0,3 |
| 14 | -0,15106142287364 | 0,143414901312537 | -0,0288250700672363 | 0,3 |
| 15 | -0,15106142287364 | -0,0288250700672363 | -0,383957885030324 | 0,3 |
| 16 | -0,383957885030324 | -0,15106142287364 | -0,226328326038328 | 0,3 |
| 17 | -0,383957885030324 | -0,226328326038328 | -0,519881278971922 | 0,3 |
| 18 | -0,519881278971922 | -0,383957885030324 | -0,507376749762318 | 0,3 |
| 19 | -0,519881278971922 | -0,507376749762318 | -0,703956634480828 | 0,3 |
| 20 | -0,703956634480828 | -0,521318017069623 | -0,507376749762318 | 0,3 |
| 21 | -0,703956634480828 | -0,521318017069623 | -0,778554392565042 | 0,3 |
| 22 | -0,778554392565042 | -0,703956634480828 | -0,681327098177849 | 0,3 |
| 23 | -0,778554392565042 | -0,816581347038974 | -0,681327098177849 | 0,3 |
| 24 | -0,816581347038974 | -0,778554392565042 | -0,743674553224567 | 0,3 |
| 25 | -0,816581347038974 | -0,842357998475409 | -0,743674553224567 | 0,3 |
| 26 | -0,845848412956476 | -0,846177360374865 | -0,838238020383463 | 0,075 |
| 27 | -0,846177360374865 | -0,845848412956476 | -0,843154372435278 | 0,075 |
| 28 | -0,846616455690446 | -0,845848412956476 | -0,843154372435278 | 0,075 |
| 29 | -0,848017017695877 | -0,847087728053341 | -0,846597987664592 | 0,0375 |
| 30 | -0,848017017695877 | -0,847980516275042 | -0,847811621576176 | 0,01875 |
| 31 | -0,848017017695877 | -0,848085062414109 | -0,847811621576176 | 0,01875 |
Т.к дальнейшее уменьшение α невозможно(α/2< ε) и в ε окрестности полученной на 31 шаге точке мы не получаем улучшения (уменьшения значения) функции, то примем x=0,248249999999998 и y=0,408289729858682 Z(x,y)= -0,847811621576176.
Похожие работы
... МП к некритическому экстраполированию результата считается его слабостью. Сети РБФ более чувствительны к «проклятию размерности» и испытывают значительные трудности, когда число входов велико. 5. МОДЕЛИРОВАНИЕ НЕЙРОННЫХ СЕТЕЙ ДЛЯ ПРОГНОЗИРОВАНИЯ СТОИМОСТИ НЕДВИЖИМОСТИ 5.1 Особенности нейросетевого прогнозирования в задаче оценки стоимости недвижимости Использование нейронных сетей можно ...
... с издержками двух или трех конкурентов. Это позволит выявить конкурентоспособность предприятия, определить имеющиеся резервы для снижения издержек. Подобный сравнительный анализ издержек производства на данном предприятии и предприятиях-конкурентах служит основанием для разработки и проведения стратегических мероприятий по снижению издержек производства и оптимизации производственной программы. ...
... от года-x и от номера месяца в году-y следующим образом: F(x)=50-x2+10x-y2+10y. Определите, в каком году и в каком месяце прибыль была максимальной. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МЕТОДЫ ОПТИМИЗАЦИИ Билет № 22 1) Постановка вариационной задачи с ограничениями. Привести пример. 2) Дайте геометрическую ...
... ) аппарат, а затем полученную величину корректируют с учетом других факторов (долгосрочная стратегия предприятия, ограничения по производственным мощностям и пр). 3. Рекомендации по оптимизации величины себестоимости продукции на основе анализа соотношения "затраты - объем - прибыль" 3.1 Деление затрат на постоянные и переменные части и определение показателей маржинального дохода ...

0 комментариев