Навигация
Метод Ньютона(метод касательных)
1.2 Метод Ньютона(метод касательных)
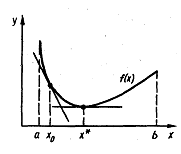
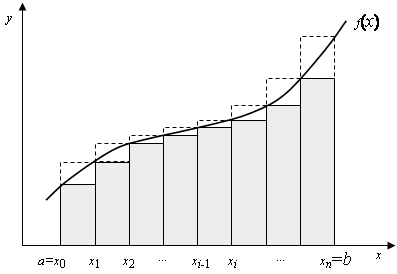
Его отличие от предыдущего метода состоит в том , что на n-й итерации вместо хорды проводится касательная к кривой y =F(x) при х=cn-1 и ищется точка пересечения касательной с точкой абсцисс. При этом необязательно задавать отрезок [a,b], содержащий корень уравнения , а достаточно лишь найти некоторое начальное приближение корня х.
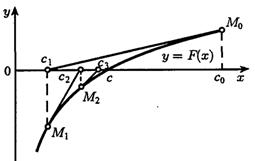
Рисунок 2. Метод касательных
Уравнение касательной, проведенной к кривой y =F(x) в некоторой точке с координатами х0 и F(х 0) имеет вид
y-F(х0)=F’(х0)(x-х0).
Отсюда найдем следующее приближение корня х как абсциссу точки пересечения касательной с осью х (у=0):
х=х0 - F(х0) /F’(х0).
Аналогично могут быть найдены и следующие приближения как точки пересечения с осью абсцисс касательных . Формула для n-го приближения имеет вид
хn=хn-1 - F(хn-1) /F’(хn-1), n=1,2,…
При этом необходимо , чтобы выполнялось условие F’(хn-1)![]() 0.
0.
Для окончания итерационного процесса используются те же условия, что и в методе хорд.
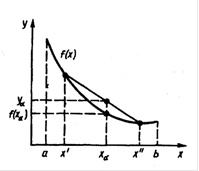
1.3 Практическое применение метода хорд для решения уравнений
Возьмем для исследования функцию ![]() и определим точность решения как
и определим точность решения как![]() =0,001.
=0,001.
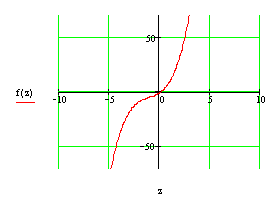
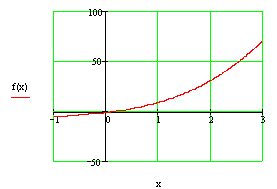
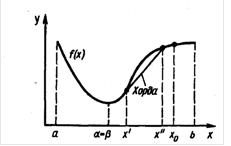
Рисунок 3. График функции ![]() (в разных пределах)
(в разных пределах)
Визуально определяем границы отрезка, на котором находится корень. Выделяем отрезок [a,b], (а=-0,1, b=0.35).
Прежде чем начать итерационный процесс, необходимо проверить функцию на данном отрезке на ряд условий:
Проверяем существование корня на отрезке по условию ![]()
f(-0.1)=-1.571
f(0.35)=1.51037
![]()
-2,37280.4954<0
Условие выполнено, следовательно на данном промежутке корень есть.
Исследуем функцию на монотонность на отрезке :![]()
![]()
![]()
![]()
![]()
![]()
Экстремумов на выбранном отрезке нет.
Проверяем функцию на единственность корня на отрезке.
![]()
![]()
![]()
![]()
![]()
43.74>0
На данном промежутке имеется только один корень.
4. Выбор точки х0 зависит от того совпадает ли её знак со знаком второй производной данной функции.
![]()
Точка а условию не удовлетворяет.
![]()
Из условия следует , что х0=b=0.35, тогда за х1 принимаем a = х1=-0.1
6. Формула для решения
![]()
При решении мы получили следующие результаты:
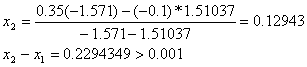
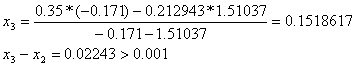
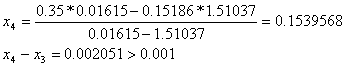
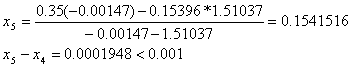
Условие![]() , где n=5 выполнено, необходимая точность достигнута, поэтому итерационный процесс можно прекратить.
, где n=5 выполнено, необходимая точность достигнута, поэтому итерационный процесс можно прекратить.
Добиться указанной точности нам удалось на 5-ой проведенной итерации.
1.4 Практическое применение метода касательных для решения уравнений
В качестве примера решим вышеупомянутое уравнение методом касательных:
![]()
![]() =0,001.
=0,001.
Начальное условие:
![]() (выбрали по тому же правилу, которое использовали для решения уравнения методом хорд
(выбрали по тому же правилу, которое использовали для решения уравнения методом хорд ![]() )
)
Применим формулу
![]()
![]()
![]() ;
;
![]()
![]()
![]()
![]()
![]()
![]() <
<![]() - необходимая точность достигнута, итерационный процесс можно останавливать.
- необходимая точность достигнута, итерационный процесс можно останавливать.
Добиться указанной точности нам удалось на 3-й проведенной итерации
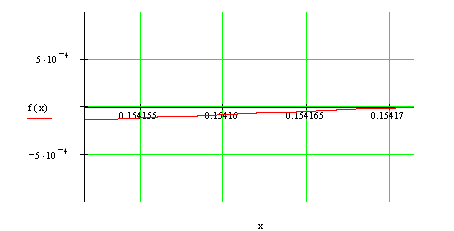
Рисунок 4. График функции на отрезке [![]() ;
; ![]() ]
]
Наименьшим полученным отрезком, в котором содержится корень уравнения является
[![]() ;
; ![]() ].
].
Значения исходной функции на концах этого отрезка
f(![]() )=-0,0001391
)=-0,0001391
f(![]() )=0,000000033
)=0,000000033
Как мы видим, на каждой итерации объем вычислений в методе касательных больший, чем в методе хорд, так как приходится находить не только функции F(х) , но и ее производной. Однако скорость сходимости значительно выше в методе касательных: в методе касательных условие сходимости выполнилось на 3- м шаге, а в методе хорд на 5-м.
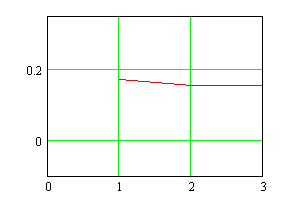
Рисунок 5. График функции ![]() для метода касательных
для метода касательных
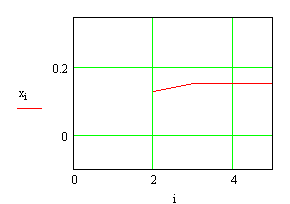
Рисунок 6. График функции ![]() для метода хорд
для метода хорд
Говоря о функции х=![]() , - выбрав начальное приближение х0 (для метода касательных), х0 и x1(для метода хорд) строится последовательность хn стремящаяся к
, - выбрав начальное приближение х0 (для метода касательных), х0 и x1(для метода хорд) строится последовательность хn стремящаяся к ![]() и условием сходимости здесь является
и условием сходимости здесь является ![]() ,т.е. тангенс угла наклона касательной должен быть меньше 1(угол должен составлять менее 45 градусов). Исходя из рисунков 5,6 очевидно что условие сходимости (
,т.е. тангенс угла наклона касательной должен быть меньше 1(угол должен составлять менее 45 градусов). Исходя из рисунков 5,6 очевидно что условие сходимости (![]() ) итерационной процедуры было выполнено.
) итерационной процедуры было выполнено.
Похожие работы
... уравнений (2) сводится к последовательному решению двух следующих систем уравнений с треугольными матрицами коэффициентов L Y = B; (6) U X = Y (7) линейный алгебраический уравнение численный где Y = - вектор вспомогательных переменных. Такой подход позволяет многократно решать системы линейных ...
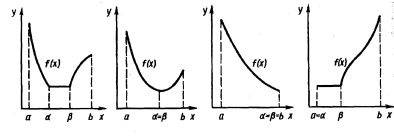
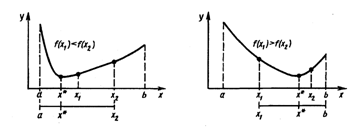
... 4 - график унимодальной, но не выпуклой функции Таким образом, кроме перечисленных свойств, выпуклые функции обладают также и всеми свойствами унимодальных функций. 2. Прямые методы безусловной оптимизации Для решения задачи минимизации функции f (х) на отрезке [а; b] на практике, как правило, применяют приближенные методы. Они позволяют найти решение этой задачи с необходимой точностью ...
... – остаточный член, характеризующий погрешность формулы. Заметим, что формулы вида (2) называют квадратурными формулами. Геометрический смысл численного интегрирования состоит в вычислении площади криволинейной трапеции, ограниченной графиком функции f(х), осью абсцисс и двумя прямыми х = а и х = b. Приближенное вычисление площади приводит к отбрасыванию в квадратурных формулах остаточного члена ...
... задачи, а именно: 1. Создана расчетная схема анализа на основании сравнительного анализа численных методов, а также программных и технических средств их осуществления; 2. Создан выбор метода автоматизированного анализа объекта проектирования; 3. Спланирован и проведен эксперимент, анализируя результаты которого, приходим к выводу, что данная модель может использоваться с параметрами: r = 5 R = ...

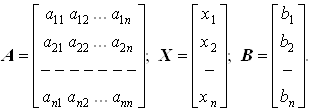






0 комментариев