Метод Ньютона(метод касательных)
Программная реализация итерационных методов
Метод простой итерации
Практическое применение метода Зейделя для решения системы уравнений
Программная реализация итерационных методов
Метод Эйлера
Практическое применение метода Эйлера для ОДУ
Практическое применение уточненного метода Эйлера для ОДУ
Навигация
Практическое применение метода Зейделя для решения системы уравнений
Сравнительный анализ численных методов
28788
знаков
6
таблиц
29
изображений
3.4 Практическое применение метода Зейделя для решения системы уравнений
Решим ту же систему линейных уравнений методом Зейделя с той же точностью : 
.
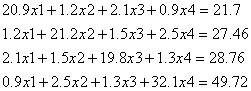
Проверку на условие сходимости мы выполнили ранее, при решении методом простых итерации.
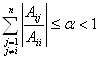
Проверим выполняется ли условие остановки итерационного процесса:
:
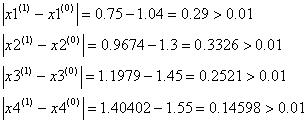
Условие остановки на первом шаге итерации не было выполнено, поэтому продолжаем итерацию, вычисляя x(2) :
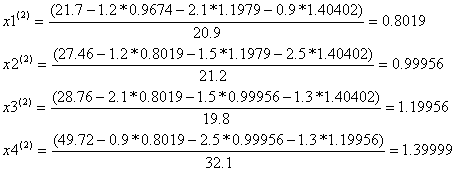
Проверим выполняется ли условие остановки итерационного процесса:
:
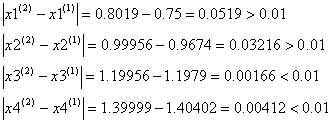
Условие остановки на втором шаге итерации было выполнено лишь для x3, x4, поэтому продолжаем итерацию, вычисляя x(3) :
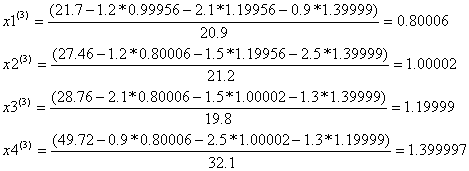
Проверим выполняется ли условие остановки итерационного процесса:
:
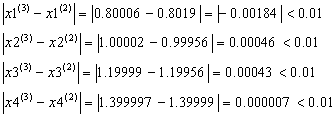
Условие сходимости выполнено на 3-ем шаге .
Корнями уравнения можно принять:
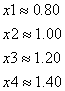
Как видно из вышеизложенных вычислений, скорость сходимости итерационного метода Зейделя выше, чем скорость сходимости метода простой итерации.
Ниже приведена сравнительная таблица1, позволяющая сравнить результаты решения СЛАУ методом простой итерации и методом Зейделя на различных шагах итерации:
Таблица1. Сводная таблица значений элементов приближений двух методов итерации
| № шага | Метод постой итерации | Метод Зейделя |
| 0 | X1=1.04 X2=1.3 X3=1.45 X4=1.55 | X1=1.04 X2=1.3 X3=1.45 X4=1.55 |
| 1 | X1=0.75 X2=0.95 X3=1.14 X4=1.36 | X1=0.75 X2=0.9674 X3=1.1976 X4=1.40402 |
| 2 | X1=1.8106 X2=1.0117 X3=1.2117 X4=1.4077 | X1=0.8019 X2=0.99956 X3=1.19956 X4=1.39999 |
| 3 | X1=0.7978 X2=0.9977 X3=1.1975 X4=1.3983 | X1=0.80006 X2=0.00002 X3=1.19999 X4=1.39997 |
| 4 | X1=0.80046 X2=0.000502 X3=1.20052 X4=1.40034 |
Похожие работы
... уравнений (2) сводится к последовательному решению двух следующих систем уравнений с треугольными матрицами коэффициентов L Y = B; (6) U X = Y (7) линейный алгебраический уравнение численный где Y = - вектор вспомогательных переменных. Такой подход позволяет многократно решать системы линейных ...
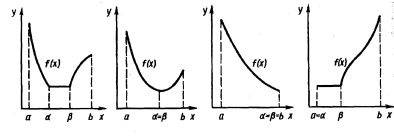
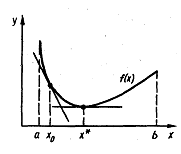
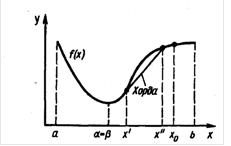
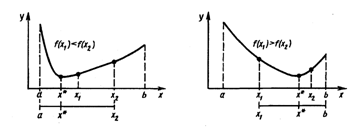
... 4 - график унимодальной, но не выпуклой функции Таким образом, кроме перечисленных свойств, выпуклые функции обладают также и всеми свойствами унимодальных функций. 2. Прямые методы безусловной оптимизации Для решения задачи минимизации функции f (х) на отрезке [а; b] на практике, как правило, применяют приближенные методы. Они позволяют найти решение этой задачи с необходимой точностью ...
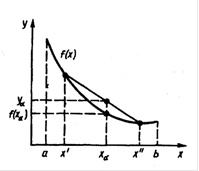
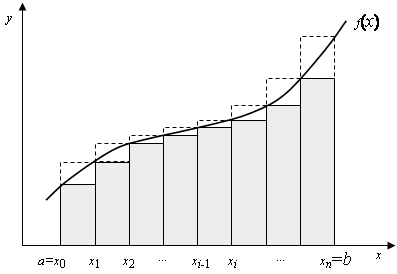
... – остаточный член, характеризующий погрешность формулы. Заметим, что формулы вида (2) называют квадратурными формулами. Геометрический смысл численного интегрирования состоит в вычислении площади криволинейной трапеции, ограниченной графиком функции f(х), осью абсцисс и двумя прямыми х = а и х = b. Приближенное вычисление площади приводит к отбрасыванию в квадратурных формулах остаточного члена ...
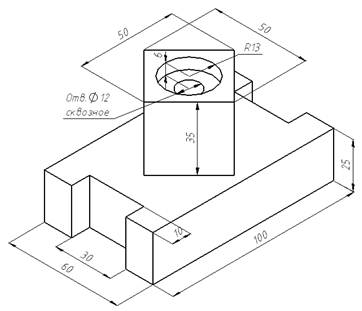
... задачи, а именно: 1. Создана расчетная схема анализа на основании сравнительного анализа численных методов, а также программных и технических средств их осуществления; 2. Создан выбор метода автоматизированного анализа объекта проектирования; 3. Спланирован и проведен эксперимент, анализируя результаты которого, приходим к выводу, что данная модель может использоваться с параметрами: r = 5 R = ...
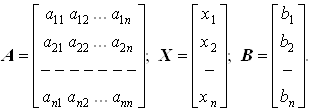
0 комментариев