Навигация
Практическое применение метода Эйлера для ОДУ
4.3 Практическое применение метода Эйлера для ОДУ
Исходное ОДУ:
![]() y(0.6)=1.2,
y(0.6)=1.2, ![]()
Таблица 1. метод Эйлера (n=5)
| i | xi | yi | f(xi,yi) |
| 0 | 0.6 | 1.2 | 0.953971 |
| 1 | 0.8 | 1.3907942 | 1.2071579 |
| 2 | 1 | 1.6322258 | 1.4725082 |
| 3 | 1,2 | 1.9267274 | 1.7488018 |
| 4 | 1,4 | 2.2764878 | 2.0337464 |
| 5 | 1,6 | 2.6832371 | 2.3236155 |
Таблица 2. метод Эйлера (n=20)
| i | xi | yi | f(xi,yi) |
| 0 | 0.6 | 1.2 | 0.953971 |
| 1 | 0.65 | 1.2476986 | 1.0173845 |
| 2 | 0.7 | 1.2985678 | 1.0816058 |
| 3 | 0.75 | 1.3526481 | 1.1466263 |
| 4 | 0.8 | 1.4099794 | 1.2124345 |
| 5 | 0.85 | 1.4706011 | 1.2790158 |
| 6 | 0.9 | 1.5345519 | 1.3463522 |
| 7 | 0,95 | 1.6018695 | 1.414422 |
| 8 | 1 | 1.6725906 | 1.4831991 |
| 9 | 1,05 | 1.7467506 | 1.5526532 |
| 10 | 1,1 | 1.8243832 | 1.6227488 |
| 11 | 1,15 | 1.9055207 | 1.6934454 |
| 12 | 1,2 | 1.9901929 | 1.7646967 |
| 13 | 1,25 | 2.0784278 | 1.8364504 |
| 14 | 1,3 | 2.1702503 | 1.9086477 |
| 15 | 1,35 | 2.2656827 | 1.981223 |
| 16 | 1,4 | 1.4490611 | 1.8231403 |
| 17 | 1,45 | 1.5402182 | 1.8978804 |
| 18 | 1,5 | 1.6351122 | 1.9732751 |
| 19 | 1,55 | 1.7337759 | 2.0492675 |
| 20 | 1,6 | 1.8362393 | 2.1257929 |
Похожие работы
... уравнений (2) сводится к последовательному решению двух следующих систем уравнений с треугольными матрицами коэффициентов L Y = B; (6) U X = Y (7) линейный алгебраический уравнение численный где Y = - вектор вспомогательных переменных. Такой подход позволяет многократно решать системы линейных ...
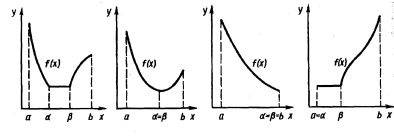
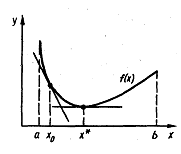
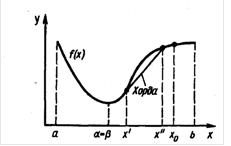
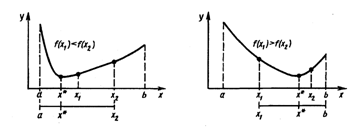
... 4 - график унимодальной, но не выпуклой функции Таким образом, кроме перечисленных свойств, выпуклые функции обладают также и всеми свойствами унимодальных функций. 2. Прямые методы безусловной оптимизации Для решения задачи минимизации функции f (х) на отрезке [а; b] на практике, как правило, применяют приближенные методы. Они позволяют найти решение этой задачи с необходимой точностью ...
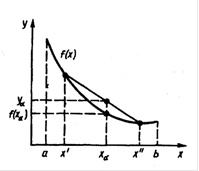
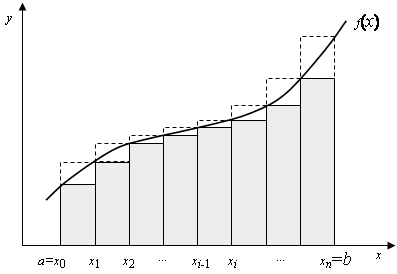
... – остаточный член, характеризующий погрешность формулы. Заметим, что формулы вида (2) называют квадратурными формулами. Геометрический смысл численного интегрирования состоит в вычислении площади криволинейной трапеции, ограниченной графиком функции f(х), осью абсцисс и двумя прямыми х = а и х = b. Приближенное вычисление площади приводит к отбрасыванию в квадратурных формулах остаточного члена ...
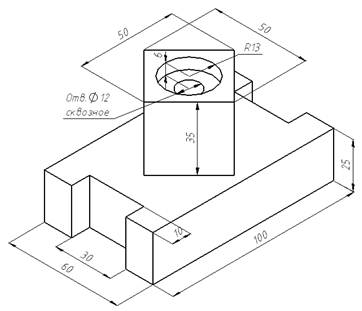
... задачи, а именно: 1. Создана расчетная схема анализа на основании сравнительного анализа численных методов, а также программных и технических средств их осуществления; 2. Создан выбор метода автоматизированного анализа объекта проектирования; 3. Спланирован и проведен эксперимент, анализируя результаты которого, приходим к выводу, что данная модель может использоваться с параметрами: r = 5 R = ...

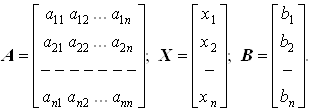






0 комментариев