Навигация
Метод простой итерации
3.1 Метод простой итерации
Этот метод широко используется для численного решения уравнений и их систем различных видов. Рассмотрим применение метода простой итерации к решению систем линейных уравнений.
Запишем исходную систему уравнений в векторно-матричном виде ![]() , где A- квадратная невырожденная матрица. Затем необходимо преобразовать систему к виду
, где A- квадратная невырожденная матрица. Затем необходимо преобразовать систему к виду
x=Bx+c,
где В- квадратная матрица с элементами bij (I,j=1,2,3…m) c- вектор-столбец с элементами ci (i=1,2,3…m)
В развёрнутой форме записи система имеет вид:
x1=b11x1+b12x2+b13x3+…b1mxm+c1
x2=b21x1+b22x2+b23x3+…b2mxm+c1
x3=b31x1+b32x2+b33x3+…b1mxm+c3
xm=bm1x1+bm2x2+bm3x3+…bmmxm+cm
Операция приведения системы к виду, удобному для итераций не является простой и требует специальных знаний. В некоторых случаях операция преобразования не имеет смысла, так как система бывает уже приведена к удобному для итераций виду.
Самым простым способом приведения системы к такому виду является тот, что описан ниже:
И первого уравнения системы выразим x1:
x1=a11-1(b1-a12x2- a13x3-…- a1mxm)
Из второго уравнения системы выразим x2:
x2=a22-1(b2-a21x2- a23x3-…- a2mxm)
xm=amm-1(bm-am1x2- am3x3-…- am-1mxm-1)
В результате получим систему:
x1=0+ b12x2+ b13x3-…+ b1m-1xm-1+ b1mxm+c1
x2= b21x2+0 +b23x3+…+ b2m-1xm-1+ b2mxm+c2
xm= bm1x1+ bm2x20 +bm3x3+…+ bmm-1xm-1+ 0+cm
в которой, на главной диагонали матрицы B находятся нулевые элементы, стальные элементы выражаются по формулам:
bij=-aij/aii ci=bi/aii (i,j=1,2,3…m, i<>j)
Итерационный процесс продолжается до тех пор , пока значения х1(k) , х2(k) , х3(k) не станут близкими с заданной погрешностью к значениям х1(k-1) , х2(k-1) , х3(k-1) .
Для возможности выполнения данного преобразования необходимо, чтобы диагональные элементы матрицы А были ненулевыми.
Часто систему преобразуют к виду x=x-![]() (Ax-b), где
(Ax-b), где ![]() -специально выбираемый числовой параметр.
-специально выбираемый числовой параметр.
Описание метода:
Выберем начальное приближение x0=( x01 x02… x0m)
подставляя его в праву часть системы
x=Bx+c,
и вычисляя полученное выражение, находим первое приближение:
x1=Bx0+c
на втором шаге подставляем приближение x1 в правую часть той же системы, получим второе приближение:
x2=Bx1+c
Продолжая этот процесс далее, получим последовательность x1 x2 x3… xn приближений, вычисляемых по формуле :
![]()
Эта формула и выражает собой метод простой итерации.
Итерационный процесс продолжается до тех пор, пока значения х(k) не станут близкими с заданной погрешностью к значениям х(k-1).
Теорема. Метод простой итерации сходится тогда и только тогда, когда все собственные числа матрицы ![]() по модулю меньше единицы, т.е.
по модулю меньше единицы, т.е. ![]() либо
либо ![]() .Эти выражения являются условиями сходимости метода итераций
.Эти выражения являются условиями сходимости метода итераций
3.2 Метод Зейделя
Метод Зейделя можно использовать как модификацию метода простых итераций. Основная идея модификации состоит в том, что при вычислении очередного (k+1)-го приближения к известному xi при i>1 используют используются уже найденные приближения к известным x1,… xi-1, а не k-е приближение как в методе простых итераций.
На (k+1)-й итерации компоненты приближения ![]() вычисляются по формулам:
вычисляются по формулам:
![]()
![]()
![]()
Условие сходимости метода Зейделя заключается в том, что матрица A системы Ax=b, должна удовлетворять условию:
модуль диагонального элемента должен быть больше суммы модулей оставшихся элементов строки или столбца.
Если данное условие выполнено, необходимо проследить, чтобы система была приведена к виду, удовлетворяющему решению методом простой итерации и выполнялось необходимое условие сходимости метода итераций:
![]() , либо
, либо ![]()
3.3 Практическое применение метода простых итераций для решения системы уравнений
Решим систему линейных уравнений методом простых итераций с точностью равной ![]() .
.
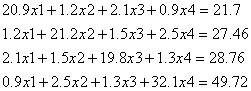
Выполним проверку на условие сходимости:
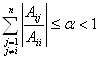
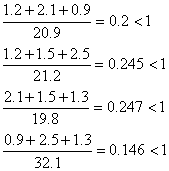
Условие выполнено, можно приступать к вычислению нулевого шага:
![]()
![]()
![]()
![]()
Начнем итерационный процесс, используя результаты начального приближения:
![]()
![]()
![]()
![]()
Проверим выполняется ли условие остановки итерационного процесса:![]() :
:
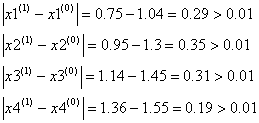
Условие остановки на первом шаге итерации не было выполнено, поэтому продолжаем итерацию, вычисляя x(2) :
![]()
![]()
![]()
![]()
Проверим выполняется ли условие остановки итерационного процесса:![]() :
:
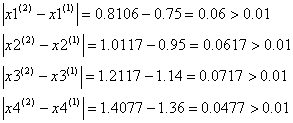
Условие остановки на втором шаге итерации не было выполнено, поэтому продолжаем итерацию, вычисляя x(3) :
![]()
![]()
![]()
![]()
Проверим выполняется ли условие остановки итерационного процесса:![]() :
:
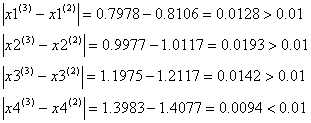
Условие остановки на третьем шаге итерации было выполнено лишь для x4, поэтому продолжаем итерацию, вычисляя x(4) :
![]()
![]()
![]()
![]()
Проверим выполняется ли условие остановки итерационного процесса:
![]()
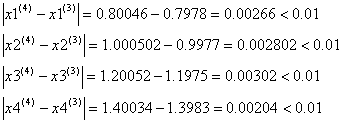
Сходимость в сотых долях имеет место уже на 4-ом шаге, тогда можно принять
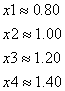
Похожие работы
... уравнений (2) сводится к последовательному решению двух следующих систем уравнений с треугольными матрицами коэффициентов L Y = B; (6) U X = Y (7) линейный алгебраический уравнение численный где Y = - вектор вспомогательных переменных. Такой подход позволяет многократно решать системы линейных ...
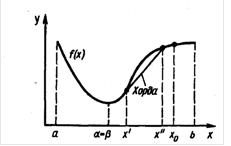
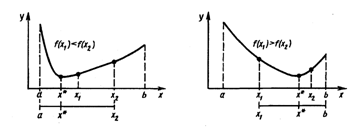
... 4 - график унимодальной, но не выпуклой функции Таким образом, кроме перечисленных свойств, выпуклые функции обладают также и всеми свойствами унимодальных функций. 2. Прямые методы безусловной оптимизации Для решения задачи минимизации функции f (х) на отрезке [а; b] на практике, как правило, применяют приближенные методы. Они позволяют найти решение этой задачи с необходимой точностью ...
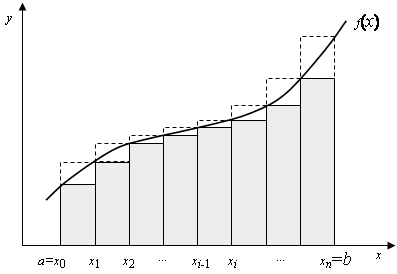
... – остаточный член, характеризующий погрешность формулы. Заметим, что формулы вида (2) называют квадратурными формулами. Геометрический смысл численного интегрирования состоит в вычислении площади криволинейной трапеции, ограниченной графиком функции f(х), осью абсцисс и двумя прямыми х = а и х = b. Приближенное вычисление площади приводит к отбрасыванию в квадратурных формулах остаточного члена ...
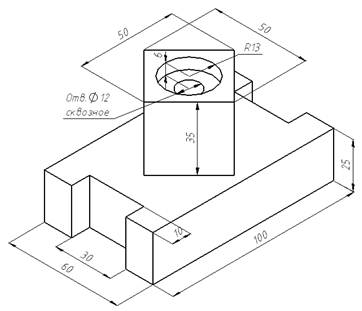
... задачи, а именно: 1. Создана расчетная схема анализа на основании сравнительного анализа численных методов, а также программных и технических средств их осуществления; 2. Создан выбор метода автоматизированного анализа объекта проектирования; 3. Спланирован и проведен эксперимент, анализируя результаты которого, приходим к выводу, что данная модель может использоваться с параметрами: r = 5 R = ...

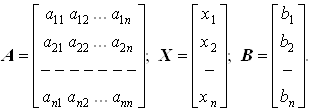






0 комментариев