Производная в направлении вектора, перпендикулярного градиенту, равна нулю
ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ
Интегралы вида
Если т и М – соответственно наименьшее и наибольшее значения функции f(x), на отрезке [a;b], то
Несобственные интегралы от неограниченных функций (несобственные интегралы ІІ рода)
Дифференциальное уравнение вида
Комплексным числом называется выражение
Уравнение вида
Конечное количество членов ряда на его сходимость не влияет
Навигация
Уравнение вида
Функция многих переменных
40147
знаков
0
таблиц
0
изображений
3. Уравнение вида
(7.11)
где р, q – постоянные числа, называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Для его решения сначала надо составить характеристическое уравнение
(7.12)
В зависимости от корней 
уравнения (7.12) общее решение уравнения (7.11) приобретает один из таких видов:
1) 
, если действительные и 
;
2) 
, если действительные и 
;
3) 
, если 
, 
(
).
Пример 7.8. Решить уравнение
(7.13)
Решение. Сначала составим и решим соответствующее характеристическое уравнение:
D = 32- 4*5= -11, 
Характеристическое уравнение имеет два сопряжённых корня:
.
Поэтому общее решение уравнения (7.13) будет таким:
.
Лекция 17. Тема – Ряды. Числовые ряды. Признаки сходимости. Степенные ряды.
План.
1. Основные понятия. Необходимое условие сходимости ряда.
2. Признаки сравнения. Признаки Даламбера и Коши. Признак Лейбница.
3. Степенные ряды. Теорема Абеля. Ряды Тейлора и Маклорена.
1. Пусть задана последовательность чисел:
Выражение
называется числовым рядом; числа 
называются членами ряда; число 
называется общим членом ряда.
Сумма п первых членов ряда
называется п-ой частичной суммой ряда.
Если существует конечный предел
,
то число S называют суммой ряда 
, а сам ряд называют сходящимся. Если же предел 
не существует или равен бесконечности, то говорят, что ряд расходящийся.
Рассмотрим ряд
.
Это сумма геометрической прогрессии, q – знаменатель прогрессии. Если 
, прогрессия называется убывающей. Сумму 
первых п членов этой прогрессии находят по формуле
.
(8.1)
Если , то 
и 
. Значит, бесконечно убывающая геометрическая прогрессия всегда сходится. Если 
, то 
и прогрессия расходится.
Если числовой ряд сходится, то разность 
между его суммой S и частичной суммой называется п-м остатком ряда, то есть
= S-.
Остаток ряда является той погрешностью, которая получится, если вместо S взять . Поскольку 
, то, взяв достаточно много первых членов сходящегося ряда, можно сумму этого ряда вычислить с любой точностью.
Отсюда становится понятным, что основной задачей теории рядов является исследование сходимости ряда. Задача нахождения суммы сходящегося ряда имеет второстепенное значений, поскольку после установления сходимости ряда его сумма может быть легко найдена.
Свойства рядов
1. Если ряды и 
сходятся и их суммы U и V, то ряд 
также сходится и его сумма равна U 
V.
2. Если ряд сходится и его сумма равна S, то ряд 
, где А=const, также сходится и его сумма равна АS.
Похожие работы
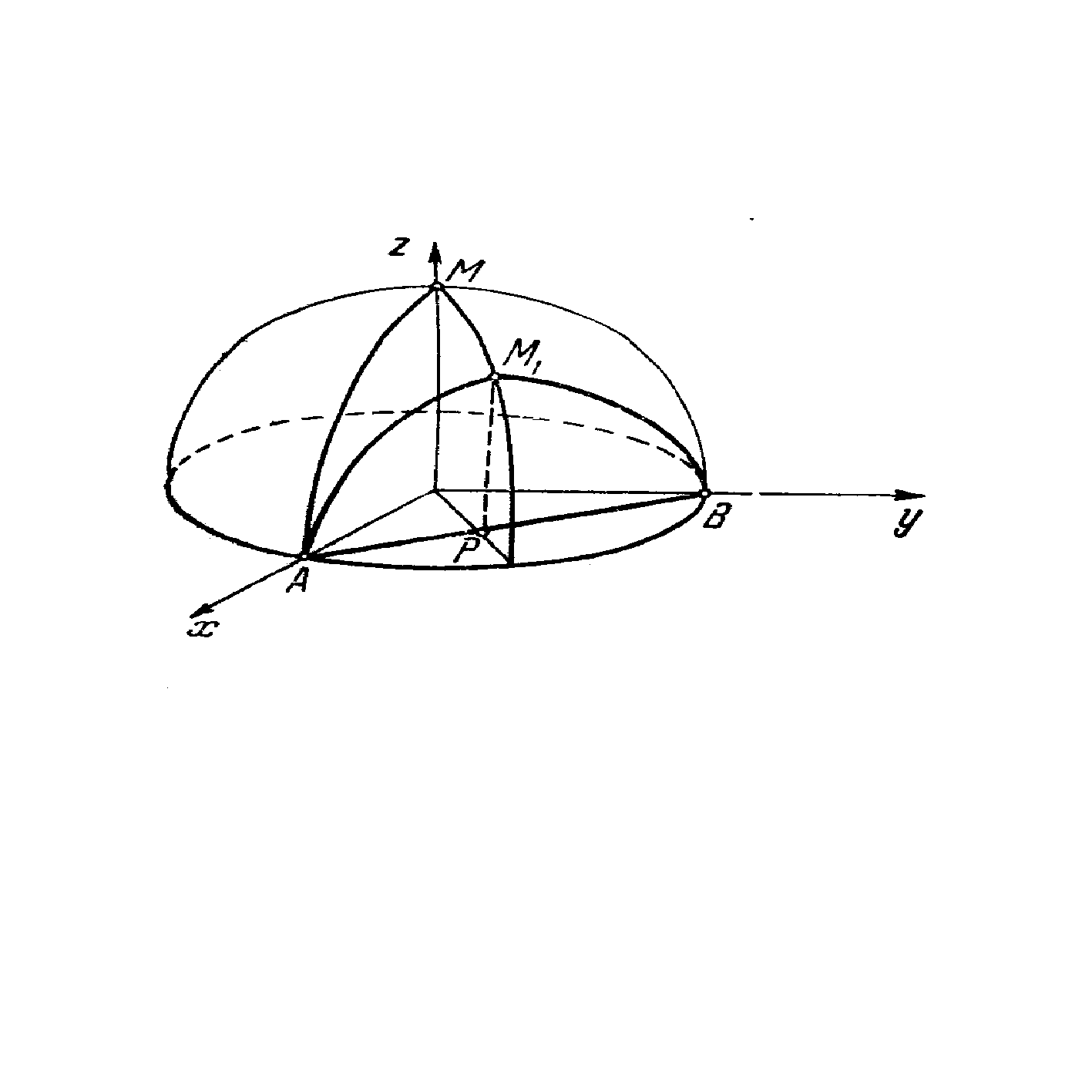
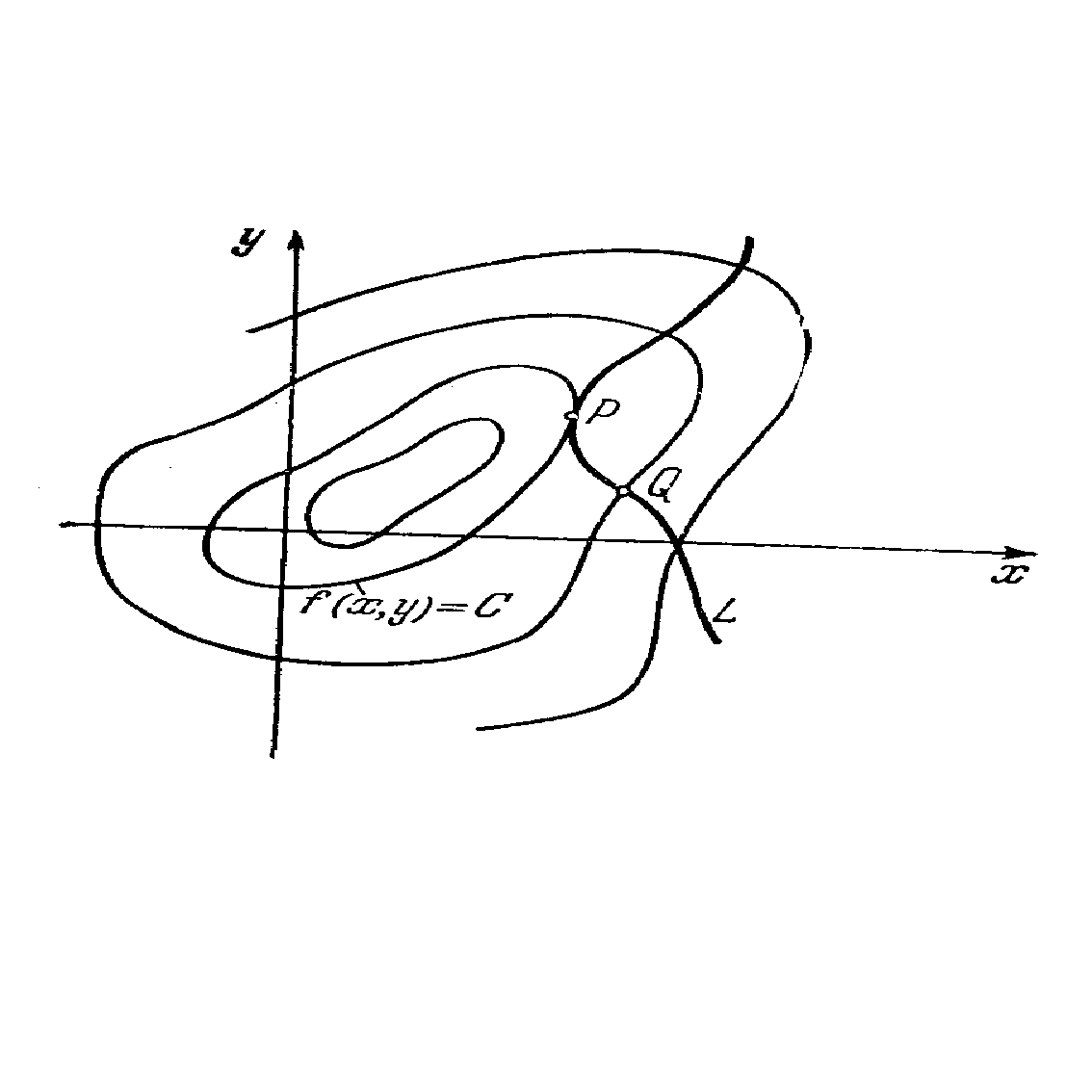
... (x, y) выполняется неравенство: . При этом, т. е. приращение функции > 0. Определение 3: Точки локальных минимума и максимума называются точками экстремума. Условные Экстремумы При отыскании экстремумов функции многих переменных часто возникают задачи, связанные с так называемым условным экстремумом. Это понятие можно разъяснить на примере функции двух переменных. Пусть заданы функция ...
... p и q, получим некоторые наборы (в зависимости от p и q) на которых функция достигает максимума. 3. Решение задачи с использованием метода покоординатного спуска 3.1 Описание метода покоординатного спуска Изложим этот метод на примере функции трех переменных . Выберем нулевое приближение . Фиксируем значения двух координат . Тогда функция будет зависеть только от одной переменной ; ...
... , Флетчера-Ривса). Методы второго порядка, использующие, кроме того, и информацию о вторых производных функции f (x) (метод Ньютона и его модификации). Метод конфигураций (Хука - Дживса) Следует выделить два этапа метода конфигураций: 1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам. Исследующий поиск начинается в точке х0, называемой старым базисом. ...
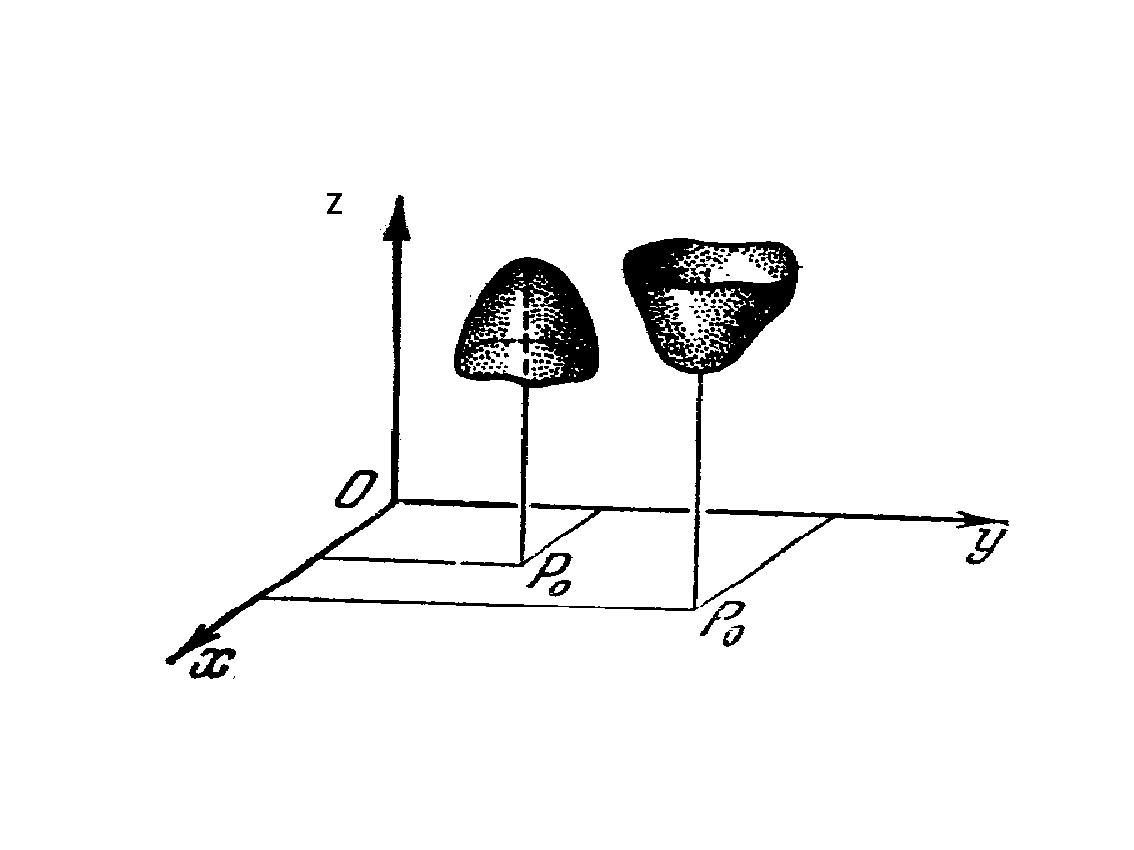
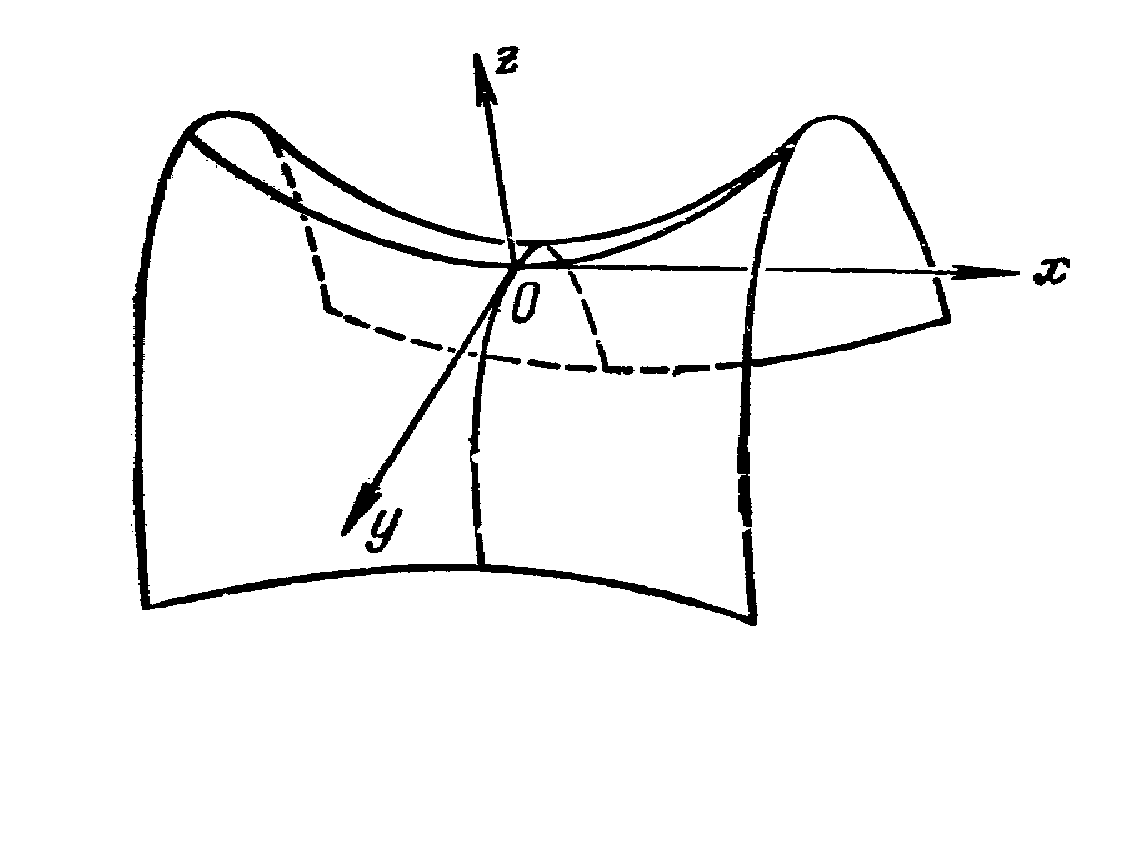
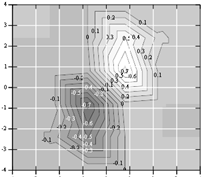
... , что и ошибки эксперимента, то итерации надо прекращать. Поскольку вблизи минимума чаще всего ~, то небольшая погрешность функции приводит к появлению довольно большой области неопределенности ~. 2. Минимум функции многих переменных 2.1 Рельеф функции Основные трудности многомерного случая удобно рассмотреть на примере функции двух переменных . Она описывает некоторую поверхность в ...
0 комментариев