Навигация
Комплексным числом называется выражение
2. Комплексным числом называется выражение
![]() ,
(7.10)
,
(7.10)
где х, у – действительные числа, а символ i – мнимая единица, которая определяется условием ![]() . При этом число х называется действительной частью комплексного числа z и обозначается
. При этом число х называется действительной частью комплексного числа z и обозначается ![]() , а у – мнимой частью z и обозначается
, а у – мнимой частью z и обозначается ![]() (от французских слов: reel – действительный, imaginare – мнимый). Выражение (7.10) называется алгебраической формой комплексного числа.
(от французских слов: reel – действительный, imaginare – мнимый). Выражение (7.10) называется алгебраической формой комплексного числа.
Два комплексных числа ![]() и
и ![]() , которые отличаются только знаком мнимой части, называются сопряжёнными.
, которые отличаются только знаком мнимой части, называются сопряжёнными.
Два комплексных числа ![]() и
и ![]() считаются равными тогда и только тогда, когда равны их действительные и мнимые части:
считаются равными тогда и только тогда, когда равны их действительные и мнимые части:
![]()
![]()
Комплексные числа можно изображать на плоскости. Так число (7.10) изображается в прямоугольной системе координат точкой М(х;у). Такая плоскость называется комплексной плоскостью переменной z, ось Ох называется действительной, у
а ось Оу – мнимой.
При у=0 комплексное число ![]() является одновременно
является одновременно
у ![]() М(х;у)
М(х;у)
действительным числом. Поэтому действительные числа являются ![]()
![]()
отдельным случаем комплексных, они изображаются на оси Ох. ![]()
![]() Комплексные числа
Комплексные числа ![]() , в которых х=0, называются чисто
, в которых х=0, называются чисто ![]()
![]()
мнимыми; такие числа изображаются на оси Оу.
0 х х
Полярные координаты точки М(х;у) на комплексной плоскости называются модулем и аргументом комплексного числа и обозначаются
![]()
Поскольку ![]() , то по формуле (7.10) имеем
, то по формуле (7.10) имеем
![]() .
.
Это выражение называется тригонометрической формой комплексного числа z.
Модуль комплексного числа определяется однозначно, а аргумент – с точностью до 2![]() :
:
![]() .
.
Здесь ![]() - общее значение аргумента, а
- общее значение аргумента, а ![]() - главное значение аргумента, которое находится на промежутке [0;
- главное значение аргумента, которое находится на промежутке [0;![]() и отсчитывается от оси Ох против часовой стрелки.
и отсчитывается от оси Ох против часовой стрелки.
Если ![]() , то считают, что
, то считают, что ![]() а
а ![]() - неопределён.
- неопределён.
Арифметические действия над комплексными числами, заданными в алгебраической форме, выполняются по обычным правилам действий над двучленами с учётом того, что ![]() . Так, если
. Так, если
![]() ,
, ![]() , то
, то
1) ![]()
2) ![]()
3) ![]()
4) 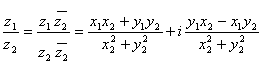 .
.
Рассмотрим действия над комплексными числами в тригонометрической форме.
Пусть
![]() ,
, ![]() .
.
Тогда
![]() =
=![]()
![]()
Значит, при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Это правило распространяется на произвольное конечное число множителей. В частности,
![]() .
.
Последняя формула называется формулой Муавра.
При делении комплексных чисел имеем
![]() .
.
Рассмотрим извлечение корня из комплексного числа. Если для данного комплексного числа ![]() надо найти корень п-й степени
надо найти корень п-й степени ![]() , то по определению корня и формуле Муавра имеем
, то по определению корня и формуле Муавра имеем
![]()
![]()
![]() .
.
Отсюда
![]() ,
, ![]() .
.
Поскольку r и ![]() положительные, то
положительные, то ![]() , где под корнем понимают его арифметическое значение. Поэтому
, где под корнем понимают его арифметическое значение. Поэтому
![]() .
.
Давая k значения 0,1,2,…, п -1, получим п разных значений корня. Для других значений k аргументы будут отличаться от найденных на число, кратное 2![]() , поэтому значения корня будут совпадать с уже найденными.
, поэтому значения корня будут совпадать с уже найденными.
Известно, что показательную функцию с мнимым показателем можно выразить через тригонометрические функции по формуле Эйлера ![]() . Отсюда следует, что всякое комплексное число можно записать в форме
. Отсюда следует, что всякое комплексное число можно записать в форме ![]() , которая называется показательной формой комплексного числа z.
, которая называется показательной формой комплексного числа z.
Похожие работы
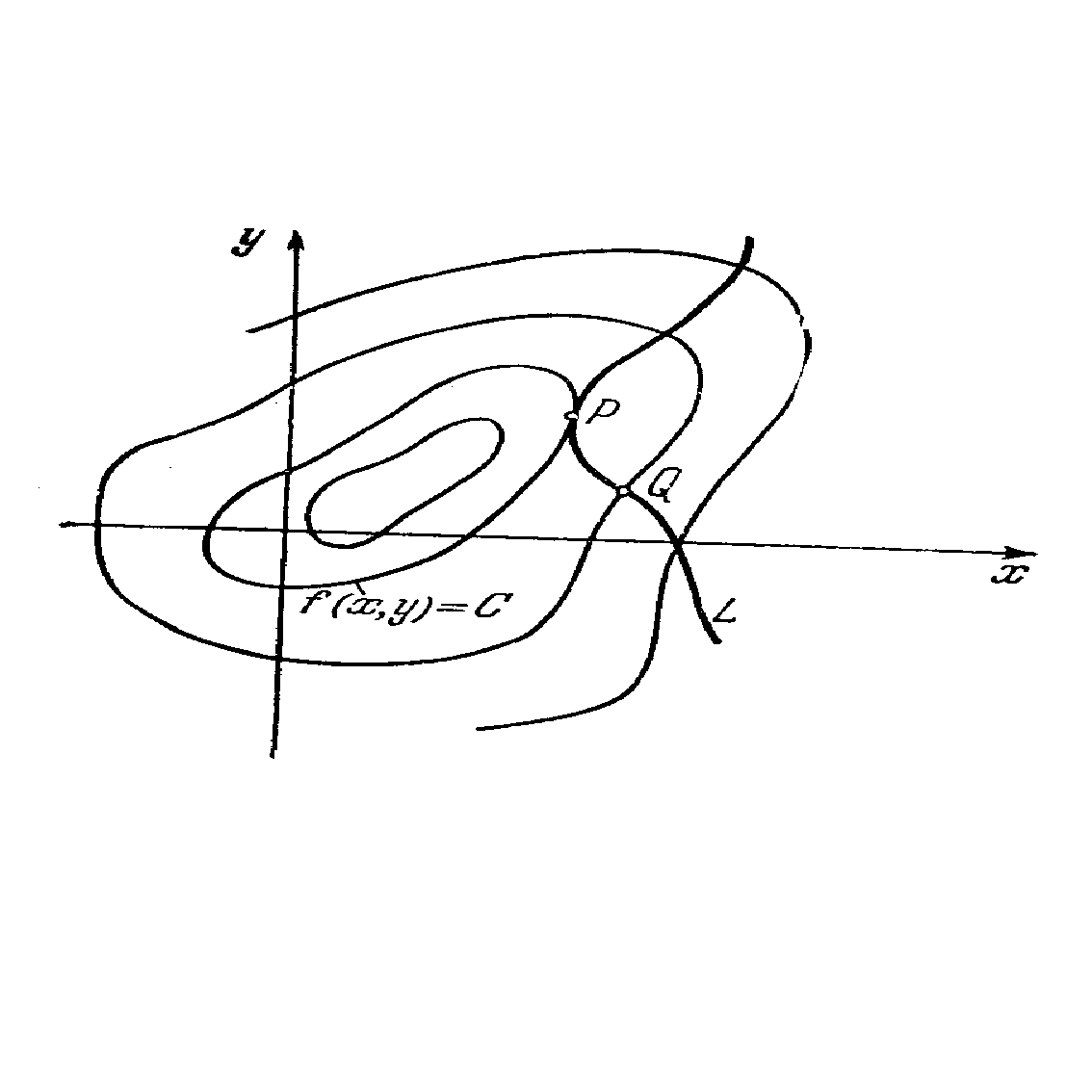
... (x, y) выполняется неравенство: . При этом, т. е. приращение функции > 0. Определение 3: Точки локальных минимума и максимума называются точками экстремума. Условные Экстремумы При отыскании экстремумов функции многих переменных часто возникают задачи, связанные с так называемым условным экстремумом. Это понятие можно разъяснить на примере функции двух переменных. Пусть заданы функция ...
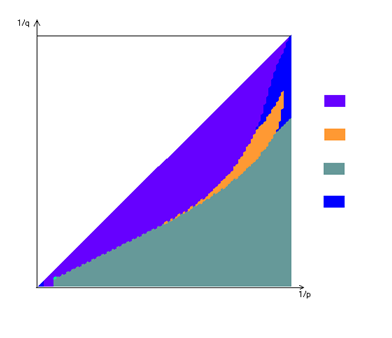
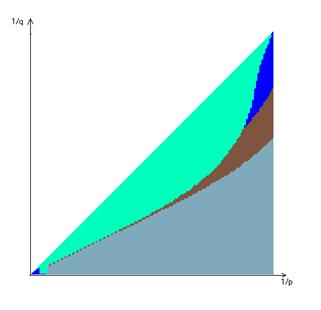
... p и q, получим некоторые наборы (в зависимости от p и q) на которых функция достигает максимума. 3. Решение задачи с использованием метода покоординатного спуска 3.1 Описание метода покоординатного спуска Изложим этот метод на примере функции трех переменных . Выберем нулевое приближение . Фиксируем значения двух координат . Тогда функция будет зависеть только от одной переменной ; ...
... , Флетчера-Ривса). Методы второго порядка, использующие, кроме того, и информацию о вторых производных функции f (x) (метод Ньютона и его модификации). Метод конфигураций (Хука - Дживса) Следует выделить два этапа метода конфигураций: 1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам. Исследующий поиск начинается в точке х0, называемой старым базисом. ...
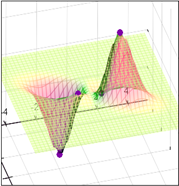
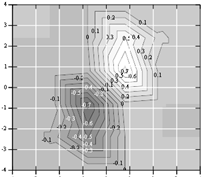
... , что и ошибки эксперимента, то итерации надо прекращать. Поскольку вблизи минимума чаще всего ~, то небольшая погрешность функции приводит к появлению довольно большой области неопределенности ~. 2. Минимум функции многих переменных 2.1 Рельеф функции Основные трудности многомерного случая удобно рассмотреть на примере функции двух переменных . Она описывает некоторую поверхность в ...

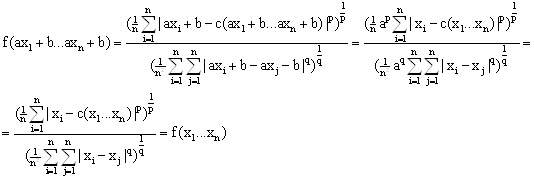

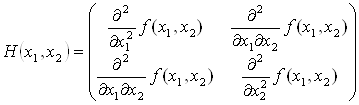


0 комментариев