Навигация
Конечное количество членов ряда на его сходимость не влияет
3. Конечное количество членов ряда на его сходимость не влияет.
Теорема 8.1. (необходимое условие сходимости ряда). Если ряд ![]() сходящийся, то предел его общего члена равен нулю
сходящийся, то предел его общего члена равен нулю
![]() .
.
Доказательство.
![]() .
.
Отсюда ![]() . Если ряд сходящийся, то
. Если ряд сходящийся, то ![]() и
и ![]() . Поэтому
. Поэтому ![]()
![]() -
-![]() - S=0.
- S=0.
Следствие. Если ![]() , то ряд
, то ряд ![]() расходящийся.
расходящийся.
Замечание. Условие ![]() является необходимым условием сходимости ряда, но не достаточным, то есть выполнение этого условия не гарантирует сходимости ряда.
является необходимым условием сходимости ряда, но не достаточным, то есть выполнение этого условия не гарантирует сходимости ряда.
Пример 8.1. Рассмотрим ряд ![]() .
.
Хотя необходимое условие сходимости ряда выполняется,
![]() ,
,
но 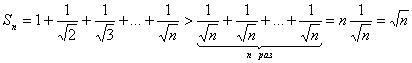 ,
, ![]()
![]()
![]() и ряд является расходящимся, несмотря на то, предел его общего члена равен нулю.
и ряд является расходящимся, несмотря на то, предел его общего члена равен нулю.
2. Первый признак сравнения. Пусть члены рядов ![]() и
и ![]() удовлетворяют условию
удовлетворяют условию
![]() п=1,2,3,… .
п=1,2,3,… .
Тогда, если ряд![]() сходящийся, то сходящийся и ряд
сходящийся, то сходящийся и ряд ![]() , а если ряд
, а если ряд ![]() расходящийся, то расходящийся и ряд
расходящийся, то расходящийся и ряд ![]() .
.
Второй признак сравнения. Пусть члены рядов ![]() и
и ![]() положительны, причём существует конечный предел
положительны, причём существует конечный предел
![]() .
.
Тогда оба ряда сходятся или расходятся одновременно.
Сравнивать ряди удобно с рядами ![]() и
и ![]() , сходимость которых известна.
, сходимость которых известна.
Ряд ![]() является суммой бесконечной геометрической прогрессии. Он сходится при
является суммой бесконечной геометрической прогрессии. Он сходится при ![]() (когда прогрессия убывающая) и расходится при
(когда прогрессия убывающая) и расходится при![]() .
.
Ряд ![]() называется обобщенным гармоническим рядом. Он сходится при
называется обобщенным гармоническим рядом. Он сходится при ![]() и расходится при
и расходится при ![]() .
.
Признак Даламбера. Если для членов ряда ![]() с положительными членами
с положительными членами ![]() существует предел
существует предел
![]() ,
,
то ряд будет сходящимся при ![]() и расходящимся при
и расходящимся при ![]() .
.
Радиальный признак Коши. Если для членов ряда ![]() с положительными членами
с положительными членами ![]() существует предел
существует предел
![]() ,
,
то ряд будет сходящимся при ![]() и расходящимся при
и расходящимся при ![]() .
.
Интегральный признак Коши. Если ![]() , где
, где ![]() - положительная невозрастающая непрерывная функция, то ряд
- положительная невозрастающая непрерывная функция, то ряд ![]() и интеграл
и интеграл ![]() сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Применим интегральный признак Коши для исследования обобщенного гармонического ряда![]() .
.
1. ![]() ,
, ![]() - гармонический ряд.
- гармонический ряд.
![]() =
=![]() ,
, ![]() =
=![]() =
=![]() - расходится.
- расходится.
2. ![]() ,
, ![]() =
=![]() ,
, 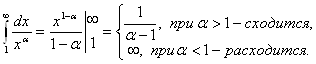
Значит, ряд ![]() сходится при
сходится при ![]() и расходится при
и расходится при ![]() .
.
Знакочередующимися называют ряды, в которых знаки членов строго чередуются
![]() , где
, где ![]() . (8.2)
. (8.2)
Признак Лейбница. Если для членов ряда (8.2) выполняется два условия:
1) ![]() .
.
2) ![]() ,
,
то этот ряд сходится, его сумма положительна и не превышает ![]() .
.
Следствие. Если сумму S сходящегося ряда (8.2) заменить суммой S![]() его п первых членов, то допущенная при этом погрешность не превышает абсолютной величины первого из отброшенных членов, то есть
его п первых членов, то допущенная при этом погрешность не превышает абсолютной величины первого из отброшенных членов, то есть
![]() .
.
Это следствие широко используется при приближённых вычислениях.
Знакопеременными называются ряды, у которых члены имеют разные знаки.
Знакопеременный ряд ![]() называется абсолютно сходящимся, если сходится ряд
называется абсолютно сходящимся, если сходится ряд ![]() , составленный из абсолютных величин его членов.
, составленный из абсолютных величин его членов.
Знакопеременный ряд называется условно сходящимся, если он сходящийся, а ряд, составленный из абсолютных величин его членов, расходящийся.
Теорема 8.2. Любой абсолютно сходящийся ряд сходится.
Для чего надо различать абсолютную и условную сходимость? Как ответ на этот сформулируем две теоремы.
Теорема 8.3. Абсолютно сходящийся ряд остаётся абсолютно сходящимся при произвольной перестановке его членов. При этом сумма ряда не зависит от порядка его членов.
Теорема 8.4. Члены условно сходящегося ряда всегда можно переставить так, чтобы его сумма равнялась наперёд заданному числу. Более того, можно так переставить члены условно сходящегося ряда, что новый ряд будет расходящимся.
Интересные свойства условно сходящихся рядов показывает такой пример.
Пример 8.2. Пусть 1-![]() .
.
Запишем ряд иначе:
![]() =
=
=![]() (1-
(1-![]() ,
,
![]()
![]() 2=1?
2=1?
Значит, переставляя члены условно сходящегося ряда, получили неверный результат.
3. Ряд ![]() , членами которого является функцией от х, называется функциональным рядом. Давая переменной х конкретные числовые значения, получим разные числовые ряды, которые могут быть сходящимися или расходящимися.
, членами которого является функцией от х, называется функциональным рядом. Давая переменной х конкретные числовые значения, получим разные числовые ряды, которые могут быть сходящимися или расходящимися.
Множество всех значений х, для которых ряд ![]() сходящийся, называется областью сходимости этого ряда.
сходящийся, называется областью сходимости этого ряда.
Функциональный ряд вида ![]() (8.3)
(8.3)
где ![]() - числа, называется степенным рядом.
- числа, называется степенным рядом.
Переобозначив ![]() на х, ряд (8.3)всегда можно свести к виду
на х, ряд (8.3)всегда можно свести к виду ![]() (8.4)
(8.4)
Для простоты будем изучать ряды вида (8.4). Ряд (8.4) всегда сходится, по крайней мере, в точке х=0.
Теорема Абеля.(1802-1829). Если ряд (8.4) сходящийся при ![]() , то он абсолютно сходящийся для всех значений х, что удовлетворяют неравенству
, то он абсолютно сходящийся для всех значений х, что удовлетворяют неравенству ![]() , то есть в интервале
, то есть в интервале ![]() . Если при
. Если при ![]() ряд (8.4) расходящийся, то он расходящийся для всех значений х, что удовлетворяют неравенству
ряд (8.4) расходящийся, то он расходящийся для всех значений х, что удовлетворяют неравенству ![]() .
.
Из теоремы Абеля следует, что если ряд (8.4) сходится хотя бы в одной точке ![]() , то существует такое число R>0, что при
, то существует такое число R>0, что при ![]() ряд сходится абсолютно, а при
ряд сходится абсолютно, а при ![]() расходится. Это число R называют радиусом сходимости степенного ряда, а интервал
расходится. Это число R называют радиусом сходимости степенного ряда, а интервал ![]() - его интервалом сходимости.
- его интервалом сходимости.
Радиус сходимости ряда (8.5) можно найти по формулам
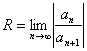 или
или  . (8.5)
. (8.5)
Вывод. Чтобы найти область сходимости ряда (8.5) надо:
1) найти интервал сходимости![]() ряда, применяя к ряду
ряда, применяя к ряду ![]() признаки Даламбера и Коши, или пользуясь формулами (8.5);
признаки Даламбера и Коши, или пользуясь формулами (8.5);
2) исследовать сходимость ряда на концах интервала сходимости, то есть в точках ![]() .
.
В середине интервала сходимости степенные ряды можно почленно интегрировать и дифференцировать, причём полученные при этом ряды будут иметь тот же радиус сходимости, что и исходный ряд.
Если функция f(х) в интервале ![]() имеет производные всех порядков и существует такое число М>0, что
имеет производные всех порядков и существует такое число М>0, что![]() ,
, ![]()
![]() , п=0, 1, 2,…, где
, п=0, 1, 2,…, где ![]() , то функцию f(х) можно разложить в ряд Тейлора
, то функцию f(х) можно разложить в ряд Тейлора
![]() .
.
При ![]() ряд Тейлора имеет вид
ряд Тейлора имеет вид
![]()
и называется рядом Маклорена.
Приведём примеры рядов Маклорена некоторых элементарных функций.
![]()
![]()
![]() ;
;
![]()
![]()
![]()
![]() ;
;
![]()
![]()
![]()
![]() ;
;
![]()
![]()
![]() ;
;
![]() =
= ![]()
![]()
![]() ;
;
![]()
![]()
![]()
![]() ;
;
Ряды широко используются для приближённого вычисления функций, интегралов, для приближённого интегрирования дифференциальных уравнений.
Похожие работы
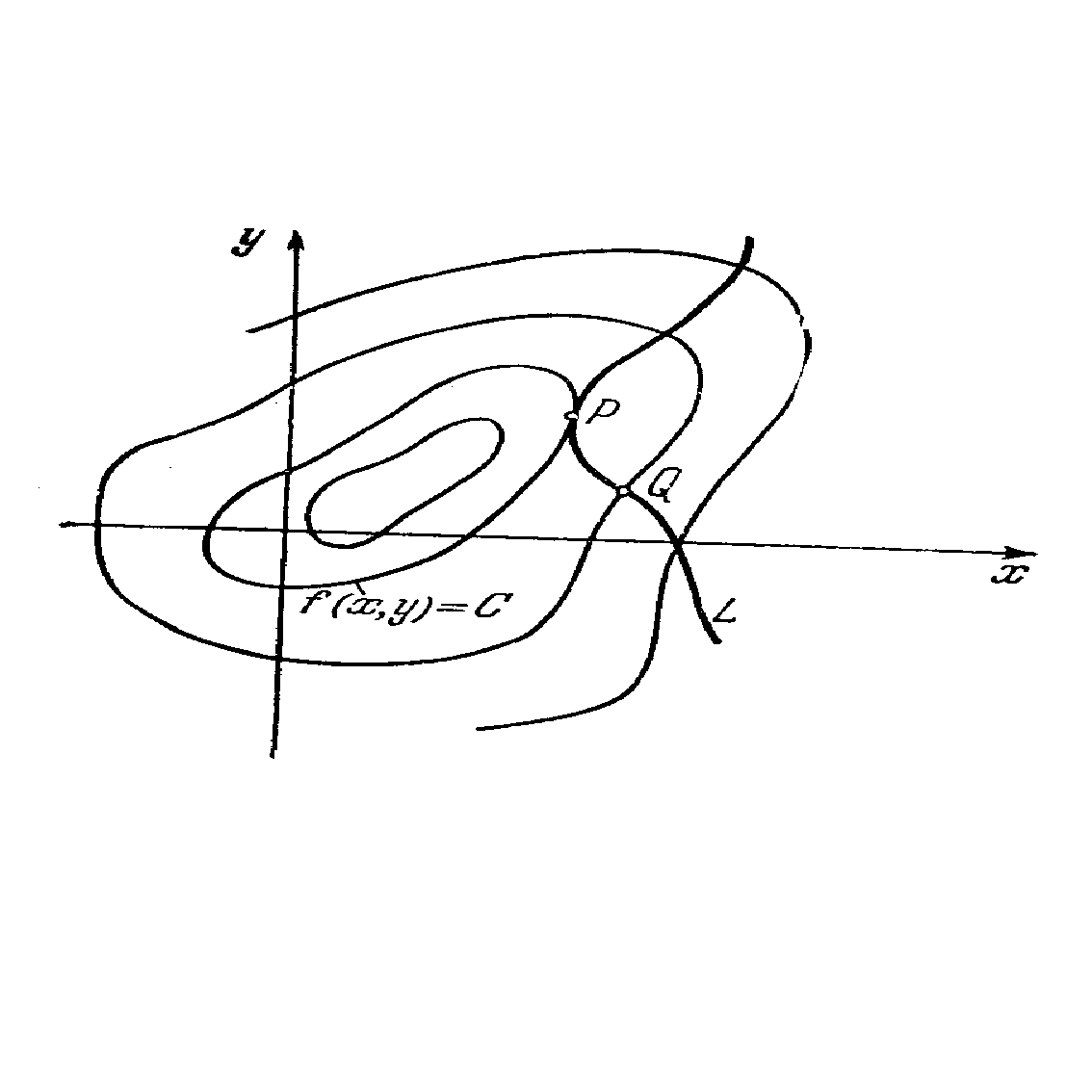
... (x, y) выполняется неравенство: . При этом, т. е. приращение функции > 0. Определение 3: Точки локальных минимума и максимума называются точками экстремума. Условные Экстремумы При отыскании экстремумов функции многих переменных часто возникают задачи, связанные с так называемым условным экстремумом. Это понятие можно разъяснить на примере функции двух переменных. Пусть заданы функция ...
... p и q, получим некоторые наборы (в зависимости от p и q) на которых функция достигает максимума. 3. Решение задачи с использованием метода покоординатного спуска 3.1 Описание метода покоординатного спуска Изложим этот метод на примере функции трех переменных . Выберем нулевое приближение . Фиксируем значения двух координат . Тогда функция будет зависеть только от одной переменной ; ...
... , Флетчера-Ривса). Методы второго порядка, использующие, кроме того, и информацию о вторых производных функции f (x) (метод Ньютона и его модификации). Метод конфигураций (Хука - Дживса) Следует выделить два этапа метода конфигураций: 1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам. Исследующий поиск начинается в точке х0, называемой старым базисом. ...
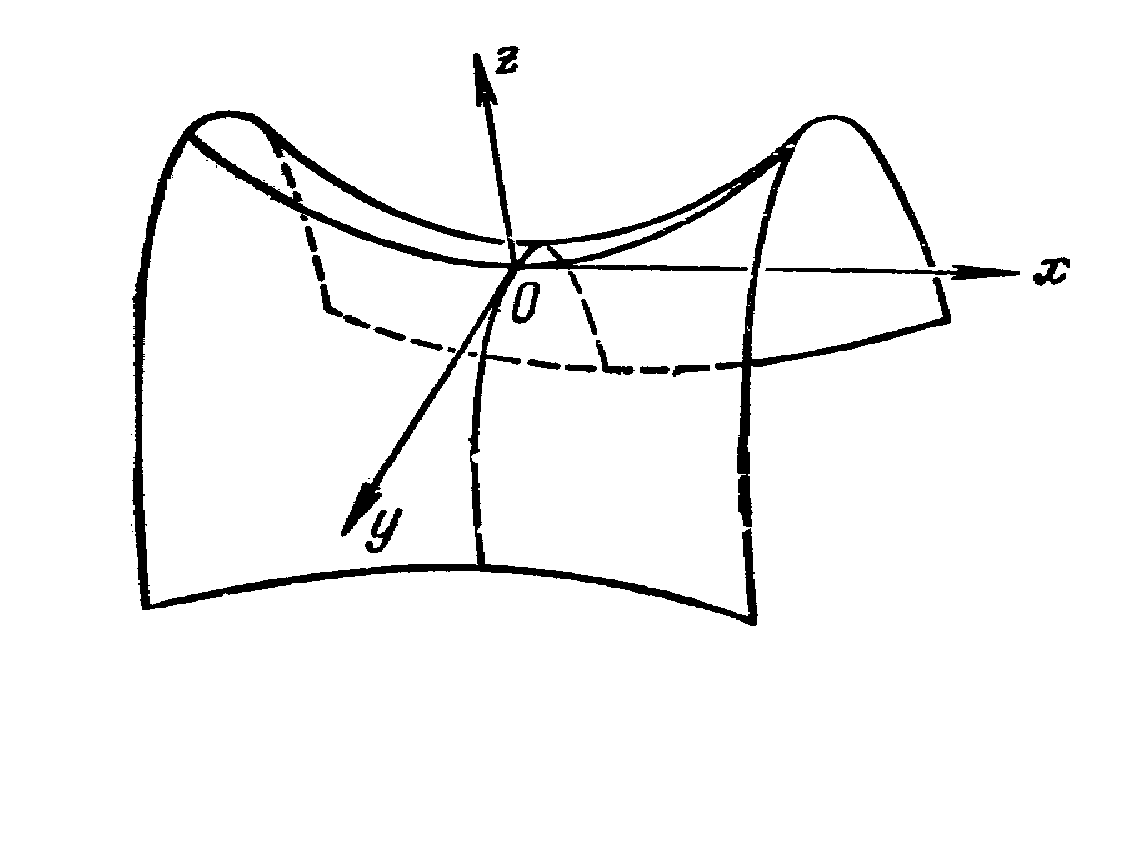
... , что и ошибки эксперимента, то итерации надо прекращать. Поскольку вблизи минимума чаще всего ~, то небольшая погрешность функции приводит к появлению довольно большой области неопределенности ~. 2. Минимум функции многих переменных 2.1 Рельеф функции Основные трудности многомерного случая удобно рассмотреть на примере функции двух переменных . Она описывает некоторую поверхность в ...

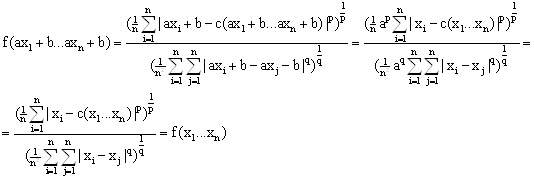



0 комментариев