Навигация
Несобственные интегралы от неограниченных функций (несобственные интегралы ІІ рода)
2. Несобственные интегралы от неограниченных функций (несобственные интегралы ІІ рода).
Если функция f(x) неограничена в любой окрестности точки с![]() (a;b) и непрерывна при
(a;b) и непрерывна при ![]() , и
, и ![]() , то по определению считают
, то по определению считают
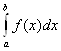 =
=![]()
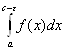 +
+ ![]()
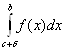 .
(6.6)
.
(6.6)
Если оба предела в правой части равенства (6.6) существуют и конечны, то несобственный интеграл считают сходящимся, в противном случае – расходящимся.
Если функция f(x) неограничена только на одном из концов отрезка [a;b], то соответствующие определения несобственного интеграла ІІ рода упрощаются:
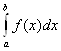 =
=![]()
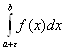 ,
,
если функция f(x) неограничена в точке х=а, и
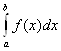 =
=![]()
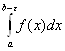 ,
,
если функция f(x) неограничена в точке х=b.
Лекция 15. Тема – Дифференциальные уравнения. Дифференциальные уравнения с разделяющимися переменными, однородные дифференциальные уравнения.
План.
1. Основные понятия.
2. Дифференциальные уравнения с разделяющимися переменными.
3. Однородные дифференциальные уравнения.
1. Дифференциальными уравнениями называют уравнения, которые содержат неизвестную функцию, её производные и аргументы.
Обыкновенным называется дифференциальное уравнение, в котором неизвестная функция является функцией одной переменной. Если неизвестная функция является функцией многих переменных, то соответствующее уравнение называется дифференциальным уравнением в частных производных.
Порядком дифференциального уравнения называется наивысший порядок производной, которая входит в это уравнение.
Пример 7.1.
1) ![]() - обыкновенное дифференциальное уравнение І порядка.
- обыкновенное дифференциальное уравнение І порядка.
2) ![]() - обыкновенное дифференциальное уравнение ІІІ порядка.
- обыкновенное дифференциальное уравнение ІІІ порядка.
3) ![]() +
+![]() =0 - дифференциальное уравнение в частных производных ІІ порядка (уравнение Лапласа).
=0 - дифференциальное уравнение в частных производных ІІ порядка (уравнение Лапласа).
Далее будем рассматривать только обыкновенные дифференциальные уравнения.
Наиболее общий вид дифференциального уравнения І порядка такой:
F(x,у,у’)=0. (7.1)
Решением этого уравнения на некотором промежутке называется дифференцированная на этом промежутке функция ![]() , которая при подстановке её в уравнение превращает его в тождество.
, которая при подстановке её в уравнение превращает его в тождество.
Пример 7.2. Решить уравнение ![]() .
.
Решение.
![]() = у,
= у, ![]() =
=![]() , ln
, ln![]() = x+ln
= x+ln![]() , у=Сех.
, у=Сех.
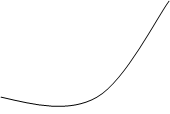
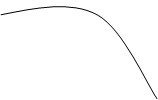
Получили множество решений.

![]() у
у
С=2
С=1
2
![]() 1 С=0
1 С=0

 0
0
-1 С= -1
-2
С=-2
Функция ![]() , где С – произвольная постоянная, называется общим решением уравнения (7.1) в области D, если:
, где С – произвольная постоянная, называется общим решением уравнения (7.1) в области D, если:
1) функция ![]() является решением уравнения (7.1) для всех значений переменной С из некоторого множества;
является решением уравнения (7.1) для всех значений переменной С из некоторого множества;
2) для произвольной точки (![]() )
) ![]() существует единственное значение С=С0, при котором функция
существует единственное значение С=С0, при котором функция ![]() удовлетворяет начальному условию
удовлетворяет начальному условию![]()
Решение ![]() , полученное из общего решения при С=С0, называется частным решением уравнения (7.1).
, полученное из общего решения при С=С0, называется частным решением уравнения (7.1).
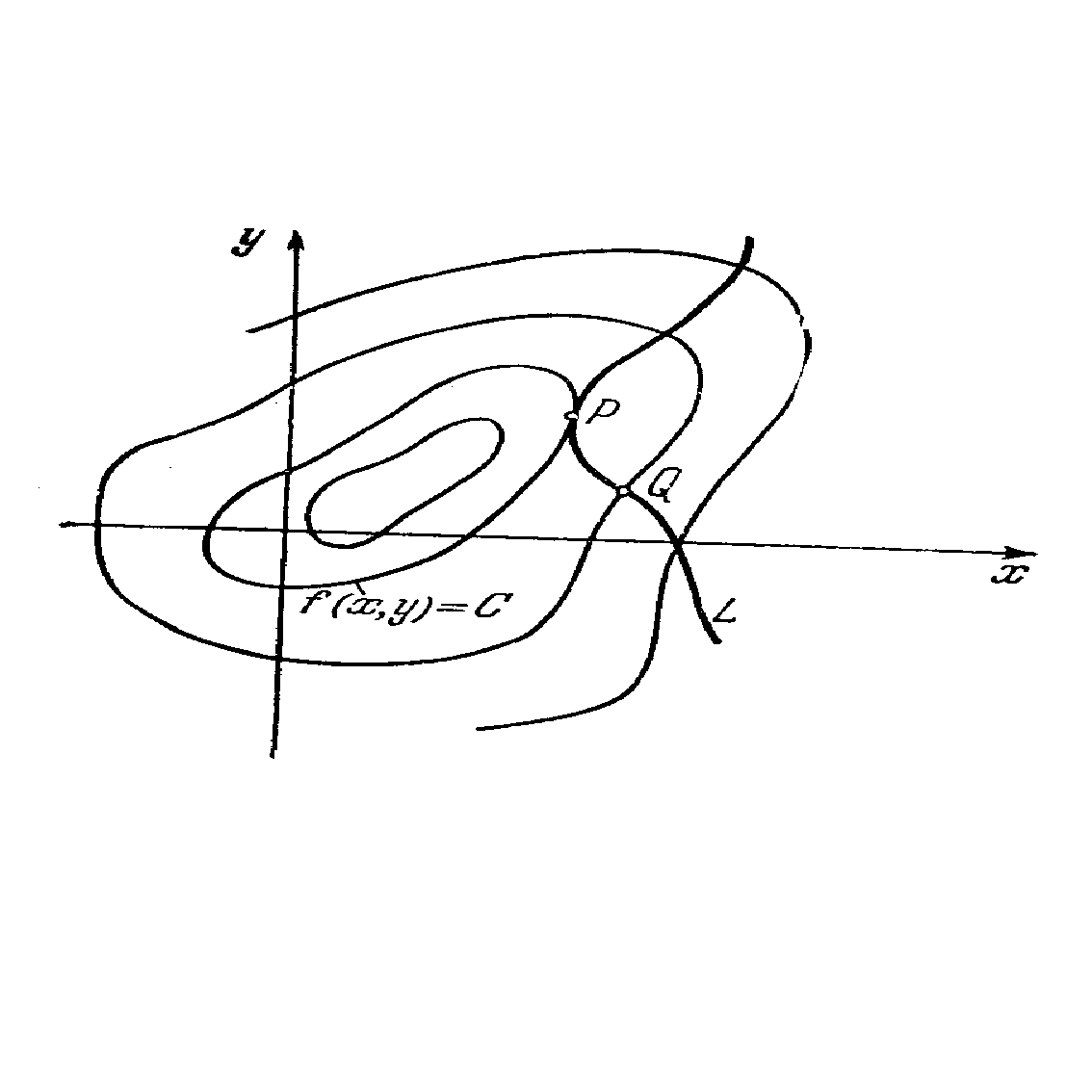
С геометрической точки зрения решение ![]() определяет некоторое бесконечное множество кривых, которые называются интегральными кривыми данного уравнения. Частное решение определяет только одну интегральную кривую, которая проходит через точку с координатами (
определяет некоторое бесконечное множество кривых, которые называются интегральными кривыми данного уравнения. Частное решение определяет только одну интегральную кривую, которая проходит через точку с координатами (![]() ).
).
Если общее решение уравнения (7.1) найдено в неявном виде Ф(х,у,С)=0, то такое решение называют общим интегралом дифференциального уравнения; равенство Ф(х,у,С0)=0 называют частным интегралом дифференциального уравнения.
Значит, для уравнения (7.1) можно поставить две задачи:
1) найти общее решение ![]() уравнения (7.1);
уравнения (7.1);
2) найти частное решение ![]() уравнения (7.1), которое удовлетворяет начальному условию
уравнения (7.1), которое удовлетворяет начальному условию ![]() .
.
Вторая задача называется задачей Коши для обыкновенного дифференциального уравнения І порядка.
Пример 7.3. Решить задачу Коши
![]() , у(0)=2.
, у(0)=2.
Решение. Сначала ищем общее решение дифференциального уравнения: у=Сех.
Из начального условия имеем: 2= Се0 ![]()
![]() .
.
Решением задачи Коши является такая функция: у=2ех.
Если уравнение (7.1) можно решить относительно у’, то его записывают в виде
![]()
и называют уравнением первого порядка, решенным относительно производной, или уравнением в нормальной форме.
Теорема 7.1 (существования и единственности решения задачи Коши). Если функция ![]() непрерывна в некоторой области D, которая содержит точку М
непрерывна в некоторой области D, которая содержит точку М![]() (
(![]() ), то задача Коши
), то задача Коши
![]() ,
, ![]()
имеет решение. Если, кроме этого, в точке М![]() непрерывна частная производная
непрерывна частная производная ![]() , то это решение единственное.
, то это решение единственное.
Процесс нахождения решений дифференциальных уравнений называется интегрированием этих уравнений. Если этот процесс сводится к алгебраическим операциям и вычислению конечного числа интегралов и производных, то говорят, что уравнение интегрируется в квадратурах. Однако класс таких уравнений очень ограничен. Поэтому для решения дифференциальных уравнений широко применяют разные приближённые методы интегрирования дифференциальных уравнений с использованием вычислительной техники.
Рассмотрим некоторые типы уравнений, интегрируемых в квадратурах.
Похожие работы
... (x, y) выполняется неравенство: . При этом, т. е. приращение функции > 0. Определение 3: Точки локальных минимума и максимума называются точками экстремума. Условные Экстремумы При отыскании экстремумов функции многих переменных часто возникают задачи, связанные с так называемым условным экстремумом. Это понятие можно разъяснить на примере функции двух переменных. Пусть заданы функция ...
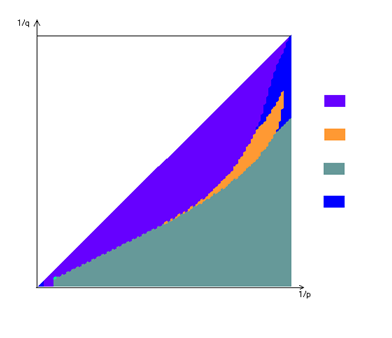
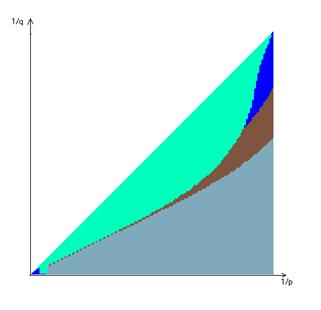
... p и q, получим некоторые наборы (в зависимости от p и q) на которых функция достигает максимума. 3. Решение задачи с использованием метода покоординатного спуска 3.1 Описание метода покоординатного спуска Изложим этот метод на примере функции трех переменных . Выберем нулевое приближение . Фиксируем значения двух координат . Тогда функция будет зависеть только от одной переменной ; ...
... , Флетчера-Ривса). Методы второго порядка, использующие, кроме того, и информацию о вторых производных функции f (x) (метод Ньютона и его модификации). Метод конфигураций (Хука - Дживса) Следует выделить два этапа метода конфигураций: 1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам. Исследующий поиск начинается в точке х0, называемой старым базисом. ...
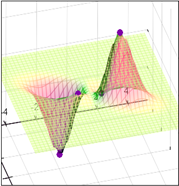
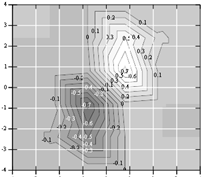
... , что и ошибки эксперимента, то итерации надо прекращать. Поскольку вблизи минимума чаще всего ~, то небольшая погрешность функции приводит к появлению довольно большой области неопределенности ~. 2. Минимум функции многих переменных 2.1 Рельеф функции Основные трудности многомерного случая удобно рассмотреть на примере функции двух переменных . Она описывает некоторую поверхность в ...

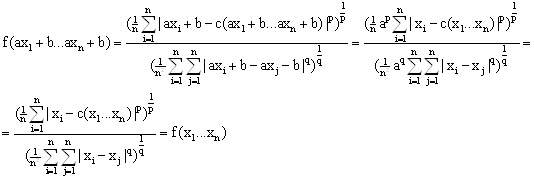

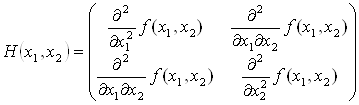


0 комментариев