Навигация
Интегралы вида
2. Интегралы вида

где R – рациональная функция, p![]() , q
, q![]() - целые числа, сводятся к интегралам от рациональных функций с помощью подстановки
- целые числа, сводятся к интегралам от рациональных функций с помощью подстановки
![]() =t
=t![]() ,
,
где п – общий знаменатель дробей ![]() ,
,![]() ,… .
,… .
3. Интегралы вида
![]() (6.1)
(6.1)
всегда сводятся к интегралам от рациональных функций с помощью, так называемой, универсальной тригонометрической подстановки
![]() ,
, ![]() ,
, ![]() ,
,
х=2arctgt, dx=![]() .
.
Замечание. Универсальная тригонометрическая подстановка всегда приводит к цели, но в силу своей универсальности она часто требует неоправданно громоздких вычислений. Поэтому во многих случаях удобнее пользоваться другими подстановками. Рассмотрим некоторые из них.
1) Если в интеграле (6.1) R(-sin x, cos x)= - R(sin x, cos x), то удобно делать подстановку cos x=t.
2) Если R(sin x,-cos x)= - R(sin x, cos x), то удобно делать подстановку sin x=t.
3) Если R(-sin x, -cos x)= R(sin x, cos x), то удобно делать подстановку
tg x=t, ![]() ,
, ![]() ,
,
х=arctgt, dx=![]() .
.
4. Рассмотрим более детально интегралы вида
![]() ,
,
где т, п – целые числа.
1) Если т – нечётное положительное число, то удобно делать подстановку cos x=t.
2) Если п – нечётное положительное число, то удобно делать подстановку sin x=t.
3) Если оба показателя т и п – чётные неотрицательные числа, то надо делать понижение степени синуса и косинуса по формулам
![]() ,
, ![]() .
.
4) Для нахождения интегралов вида
![]() ,
, ![]()
удобно пользоваться формулами
![]()
![]()
5. В интегралах
![]() ,
, ![]() ,
, ![]() ,
, ![]()
надо подынтегральную функцию записать в виде суммы функций с помощью формул
![]()
![]()
![]()
Лекция 14. Тема – Задача о площади криволинейной трапеции. Определённый интеграл его геометрический смысл и свойства.
Формула Ньютона-Лейбница.
План.
1. Задача о площади криволинейной трапеции. Определение и существование определённого интеграла.
2. Геометрический смысл определённого интеграла. Свойства определённого интеграла.
3. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
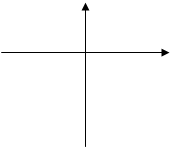
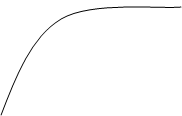 1. Криволинейной трапецией называется фигура, ограниченная линией у= f(x) и прямыми х=а, х=b, у=0. Будем считать, что f(x)
1. Криволинейной трапецией называется фигура, ограниченная линией у= f(x) и прямыми х=а, х=b, у=0. Будем считать, что f(x)![]() на [a;b].
на [a;b].
![]()
![]()
![]()
![]()
![]()
![]() у у= f(x)
у у= f(x)

0 а х![]() х
х![]()
![]() х
х![]() b x
b x
Разобьём отрезок [a;b] произвольным образом на п частей точками а=х![]() <x
<x![]() <…< х
<…< х![]() < х
< х![]() <… <х
<… <х![]() =b.
=b.
На каждом отрезке [х![]() ; х
; х![]() ] возьмём произвольную точку
] возьмём произвольную точку ![]() и вычислим значение f(
и вычислим значение f(![]() ). Тогда площадь S
). Тогда площадь S![]() заштрихованного прямоугольника, будет равна
заштрихованного прямоугольника, будет равна
S![]() = f(
= f(![]() )
)![]() , где
, где ![]() = х
= х![]() - х
- х![]() .
.
Площадь S всей трапеции приблизительно равна
S![]()
![]() .
.
Пусть ![]() . Естественно считать, что
. Естественно считать, что
S![]() .
(6.2)
.
(6.2)
К пределам вида (6.2) приводят много других задач, поэтому возникает необходимость всестороннего изучения таких пределов независимо от конкретного содержания той или иной задачи.
Пусть функция у= f(x) определена на отрезке [a;b]. Разобьём этот отрезок на п произвольных частей точками
а=х![]() <x
<x![]() <…< х
<…< х![]() < х
< х![]() <… <х
<… <х![]() =b.
=b.
На каждом из созданных отрезков [х![]() ; х
; х![]() ] возьмём произвольную точку
] возьмём произвольную точку ![]() и составим сумму
и составим сумму
![]() , где
, где ![]() = х
= х![]() - х
- х![]() ,
,
которую будем называть интегральной суммой функции f(x).
Обозначим ![]() . Если существует конечный предел интегральной суммы
. Если существует конечный предел интегральной суммы ![]() , при
, при ![]() , который не зависит ни от способа разбиения отрезка [a;b], ни от выбора точек
, который не зависит ни от способа разбиения отрезка [a;b], ни от выбора точек![]() , то этот предел называется определённым интегралом функции f(x) на отрезке [a;b] и обозначается символом
, то этот предел называется определённым интегралом функции f(x) на отрезке [a;b] и обозначается символом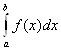 , где функция f(x) называется интегрированной на отрезке [a;b].
, где функция f(x) называется интегрированной на отрезке [a;b].
То есть, по определению,
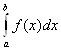 =
=![]() .
.
Числа а и b называются соответственно нижним и верхним пределом интегрирования.
Относительно существования определённого интеграла имеет место такая теорема
Теорема 6.3. Если функция f(x) ограничена на отрезке [a;b] и непрерывна на нём везде, кроме конечного числа точек, то она интегрируема на этом отрезке.
2. Если f(x)![]() , то
, то 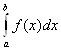 равен площади соответствующей криволинейной трапеции:
равен площади соответствующей криволинейной трапеции: 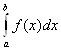 =S. Если f(x)<0, то
=S. Если f(x)<0, то 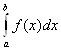 = -S.
= -S.
Отсюда следует, что если на симметричном относительно начала координат отрезке [-a;а], а>0 задана нечётная функция, то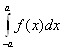 =0. Например,
=0. Например, ![]() Если функция f(x) чётная, то
Если функция f(x) чётная, то 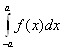 =2
=2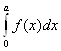 .
.
Свойства определённого интеграла
Будем считать, что все интегралы, которые рассматриваются, существуют.
1. 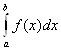 =
=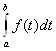 . Величина определённого интеграла не зависит от обозначения переменной интегрирования.
. Величина определённого интеграла не зависит от обозначения переменной интегрирования.
2.  =0.
=0.
3. 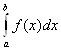 = -
= -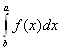 .
.
4. 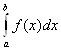 =
=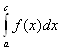 +
+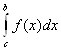 .
.
5. 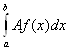 =А
=А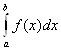 .
.
6. 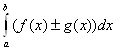 =
=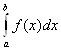
![]()
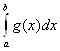 .
.
7. Если на отрезке [a;b] f(x)![]() , то
, то 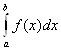
![]()
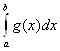 .
.
Похожие работы
... (x, y) выполняется неравенство: . При этом, т. е. приращение функции > 0. Определение 3: Точки локальных минимума и максимума называются точками экстремума. Условные Экстремумы При отыскании экстремумов функции многих переменных часто возникают задачи, связанные с так называемым условным экстремумом. Это понятие можно разъяснить на примере функции двух переменных. Пусть заданы функция ...
... p и q, получим некоторые наборы (в зависимости от p и q) на которых функция достигает максимума. 3. Решение задачи с использованием метода покоординатного спуска 3.1 Описание метода покоординатного спуска Изложим этот метод на примере функции трех переменных . Выберем нулевое приближение . Фиксируем значения двух координат . Тогда функция будет зависеть только от одной переменной ; ...
... , Флетчера-Ривса). Методы второго порядка, использующие, кроме того, и информацию о вторых производных функции f (x) (метод Ньютона и его модификации). Метод конфигураций (Хука - Дживса) Следует выделить два этапа метода конфигураций: 1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам. Исследующий поиск начинается в точке х0, называемой старым базисом. ...
... , что и ошибки эксперимента, то итерации надо прекращать. Поскольку вблизи минимума чаще всего ~, то небольшая погрешность функции приводит к появлению довольно большой области неопределенности ~. 2. Минимум функции многих переменных 2.1 Рельеф функции Основные трудности многомерного случая удобно рассмотреть на примере функции двух переменных . Она описывает некоторую поверхность в ...




0 комментариев