Навигация
Применение производной при решении уравнений
33097
знаков
0
таблиц
0
изображений
1.3. Применение производной при решении уравнений
Покажем, как с помощью производной можно решать вопросы существова-ния корней уравнения, а в некоторых случаях и их отыскания. По-прежнему основную роль здесь будут играть исследования функции на монотонность, нахождение ее экстремальных значений. Кроме того, будет использован ряд свойств монотонных и непрерывных функций.
Свойство 1. Если функция f возрастает или убывает на некотором промежутке, то на этом промежутке равнение f(x)=0 имеет не более одного корня.
Это утверждение вытекает непосредственно из определения возрастающей и убывающей функций. Корень уравнения f(x)=0 равен абсциссе точки пересечения графика функции y=f(x) с осью x.
Свойство 2. Если функция f определена и непрерывна на промежутке [a,b] и на его концах принимает значения разных знаков, то между a и b найдется точка c, в которой f(c )=0.
Задача 1.12. Решить уравнение 
Решение.
Заметим, что 
является корнем уравнения. Докажем, что других корней это уравнение не имеет. Исследуем функцию f, где 
, на монотонность. Производная 
. Установим промежутки, на которых функция 
сохраняет знак. Для этого исследуем ее на монотонность. Производная 
. Так как при 
, то 
при . Следовательно, функция возрастает при положительных значениях x; 
. Поэтому 
при . В силу четности функции 
она принимает положительные значения при всех 
. Следовательно, f возрастает на всей числовой оси. Согласно свойству 1, уравнение 
имеет не более одного корня. Итак, – единственный корень уравнения.
Задача 1.13. Решить систему уравнений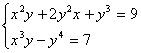 
Решение.
Система эквивалентна следующей: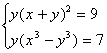 
Из первого уравнения следует, что 
, из второго – 
. Выразим з первого уравнения x через y: 
, 
. Тогда 
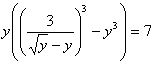. положив 
, получим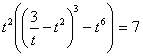 
или 
. Производная функции f, где 
, равна 
. она отрицательна при всех значениях t. Таким образом, функция f убывает. Поэтому уравнение 
имеет не более одного корня. Заметим, что 
является его корнем. Итак, 
единственное решение системы.
Задача 1.14. Доказать, что уравнение 
имеет единственный корень, лежащий в интервале 
.
Решение.
Уравнение равносильными преобразованиями приводится к виду , где 
. Функция f возрастающая, так как 
при всех 
. Согласно свойству 1, уравнение имеет не более одного решения. Функция f непрерывна, кроме того, 
, 
. В силу свойства 2 уравнение на интервале имеет корень.
В задаче 3 требовалось доказать, что корень уравнения принадлежит некоторому промежутку. Мы пользовались свойством 2 непрерывной на отрезке функции, принимающей на концах этого отрезка значения разных знаков. Этот путь не всегда приводит к цели при решении подобных задач. Иногда целесооб-разно воспользоваться следующим свойством дифференцируемых функций.
Свойство 3 (Теорема Ролля). Если функция f непрерывна на отрезке [a,b], дифференцируема на интервале (a,b) и f(a)=f(b), то существует точка 
такая, что 
.
На геометрическом языке свойство 3 означает следующее: если 
, то на графике кривой 
найдется точка С с координатами 
, где касательная к графику параллельна оси x.
Задача 1.15. Доказать, что уравнение 
при 
, 
имеет не более одного действительного корня.
Решение.
Предположим, что уравнение имеет, по крайней мере, два корня 
и 
. Функция f, где 
дифференцируема на всей числовой прямой. Так как 
, то согласно свойству 3, ее производная 
на интервале 
имеет корень. Однако при уравнение 
решений не имеет. Полученное противоречие показывает, что уравнение не может иметь более одного корня.
Задача 1.16. Доказать, что многочлен 
, 
,
имеет не более n корней.
Решение.
Согласно свойству 3, между двумя корнями многочлена лежит, по крайнем мере, один корень его производной. Поэтому, если многочлен f(x) имеет 
, различных корней, то его производная 
должна иметь не менее (k-1) корней. Точно так же 
– не менее k-2 корней и т.д., n-ая производная – не менее (k-n) корней, 
. Это невозможно, так как 
является отличной от нуля постоянной.
Задача 1.17. Доказать, что многочлен 
имеет корень между 0 и 1 (
).
Решение.
Применение свойства 2 к цели не приводит, так как 
. Рассмотрим функцию g, где 
. Для нее функция f является производной. Так как 
, то согласно свойству 3, при некотором 
.
Задача 1.18. Доказать, что уравнение 
не имеет действительных корней.
Решение.
Пусть 
, тогда 
. Если x – корень уравнения, то 
, т.е. функция f, в силу ее непрерывности, убывает в окрестности каждого корня. Заметим, что если уравнение имеет корни, то они отрицательные. Известно, что многочлен n-й степени имеет не более n корней. Обозначим через 
- наибольший из корней. Тогда существует такое 
, 
что 
. Так как 
, то на интервале 
должен находиться корень x многочлена f(x). получили противоречие.
Рассмотрим уравнение вида 
, где f, g – взаимно обратные, возрастающие функции, имеющие одинаковые области определения. Покажем, что это уравнение равносильно уравнению 
. (3)
В самом деле, пусть а является корнем уравнения (3), т.е. 
. Учитывая, что область определения функции g совпадает со множеством значений функции f им наоборот, можно записать: 
, или 
, т.е. 
, а является корнем уравнения .
Обратно, пусть , но 
. Тогда 
или 
. первом случае 
. Точно так же получается противоречие и во втором случае.
Таким образом, получен один частный прием равносильного преобразования уравнений.
Задача 1.19. Решить уравнение 
.
Решение.
Перепишем данное уравнение в виде 
. Функция 
непрерывна, возрастающая (как сумма двух возрастающих функций 
и 
), поэтому она имеет обратную. Найдем ее: 
, 
. Итак, обратной для f является функция 
, совпадающая правой частью уравнения. На основании доказанного выше уравнение эквивалентно уравнению 
. Ясно, что является корнем уравнения. Убедимся, что других корней уравнение не имеет.
Пусть 
. Тогда 
положительна как разность между средним арифметическим и средним геометрическим двух положительных чисел 
и 
.Таким образом, функция h возрастает на всей числовой оси. Так как 
, то h(x)>0 при и 
при 
, т.е. - единственный корень уравнения.
РАЗДЕЛ 2
ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ В ЗАДАЧАХ ЭЛЕМЕНТАРНОЙ МАТЕМАТИКИ
Похожие работы
... сформулированной гипотезы необходимо было решить следующие задачи: 1. Выявить роль тригонометрических уравнений и неравенств при обучении математике; 2. Разработать методику формирования умений решать тригонометрические уравнения и неравенства, направленную на развитие тригонометрических представлений; 3. Экспериментально проверить эффективность разработанной методики. Для решения ...
... точек координатной оси. Занятие № 4. Тема: Аналитический метод. Метод «ветвлений». Цель занятия: познакомить учеников с основным методом решения уравнений, содержащих параметр. Литература для учителя: см. [1] , [5], [6], [7], [14] Литература для ученика: см. [3] Краткое содержание: рассмотрение различных значений, принимаемых параметром. Упрощение уравнения и приведение уравнения к произведению ...
... по алгебре и началам анализа, при подготовке к государственной итоговой аттестации, внешнему независимому оцениванию. Достаточно большое число задач раскрывают потенциальные возможности анализа бесконечно малых величин. 1. Производная и ее применение для решения прикладных задач 1.1 Исторические сведения Ряд задач дифференциального исчисления был решен еще в древности. Они встречались у ...
... выше теорема свидетельствует о важности априорных оценок для доказательства теорем существования и единственности решений. Глава 2. Приложение Пример 1. Рассмотрим интегральное уравнение с малым вещественным параметром λ: (1) Это уравнение вида А()х = у() – операторное уравнение в С[-π; π], где Покажем, что А() аналитична в т. 0, т.е. разлагается в ряд вида . Разложим функцию ...
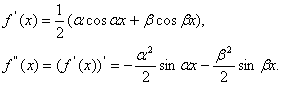
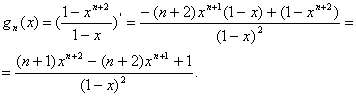
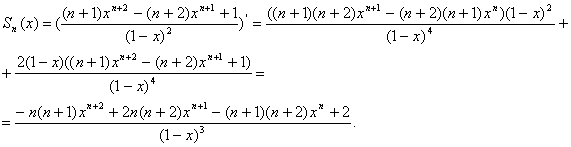
0 комментариев