Навигация
2.2. Монотонность интеграла
Из определения интеграла вытекает, что для неотрицательной непрерывной на отрезке [a,b] функции f 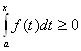 для всех
для всех ![]() .
.
Теорема 1. Пусть функции f и g непрерывны на отрезке [a,b] и для всех ![]()
![]() . Тогда для всех
. Тогда для всех ![]() :
: 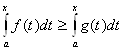 . Это свойство называют монотонностью интеграла.
. Это свойство называют монотонностью интеграла.
С помощью теоремы 1 почленно проинтегрировав обе части неравенства, можно получить целую серию новых неравенств. Например,
при ![]() имеем очевидное неравенство
имеем очевидное неравенство ![]() . Применим теорему 1, положив
. Применим теорему 1, положив ![]() . Функции f, g удовлетворяют условиям теоремы на промежутке
. Функции f, g удовлетворяют условиям теоремы на промежутке ![]() . Поэтому для произвольного
. Поэтому для произвольного ![]() :
: 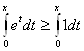 , т.е.
, т.е. ![]() (1). Применяя тот же метод к неравенству (1), получаем
(1). Применяя тот же метод к неравенству (1), получаем 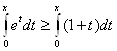 , или
, или ![]() . Отсюда
. Отсюда ![]() . Продолжая аналогично, имеем
. Продолжая аналогично, имеем ![]() ,
,
![]() и т.д.
и т.д.
В рассмотренном примере выбор исходного неравенства не составил труда. В иных случаях этот первый шаг решения задачи не столь очевиден. Теорема 1 дает, по существу, прием для получения исходного неравенства.
Пусть требуется проверить истинность неравенства
![]() (2.4)
(2.4)
Если справедливо соотношение ![]() , то согласно теореме 1, имеет место и неравенство
, то согласно теореме 1, имеет место и неравенство
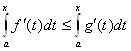 , или
, или ![]() (2.5).
(2.5).
Если имеет место неравенство ![]() , то, складывая его почленно с (2.4), устанавливаем справедливость неравенства (2.5).
, то, складывая его почленно с (2.4), устанавливаем справедливость неравенства (2.5).
Задача 2.4. Доказать, что при ![]()
![]() . (2.6)
. (2.6)
Решение.
Неравенство (2.6) перепишем в виде 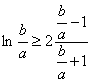 . Левая и правая части последнего неравенства представляют собой функции от
. Левая и правая части последнего неравенства представляют собой функции от ![]() . Обозначив
. Обозначив ![]() , получим
, получим ![]() (2.7). Докажем, что (2.7) выполняется при
(2.7). Докажем, что (2.7) выполняется при ![]() . Найдем производные обеих частей неравенства (2.7). Соответственно имеем:
. Найдем производные обеих частей неравенства (2.7). Соответственно имеем:
 . При
. При ![]()
![]() . Действительно,
. Действительно, ![]() . Применяя теорему 1 для функций
. Применяя теорему 1 для функций ![]() и
и ![]() при
при ![]() , получаем
, получаем ![]() . Так как
. Так как ![]() , то
, то
![]() . Отсюда при
. Отсюда при ![]() ,
, ![]() следует (2.6).
следует (2.6).
Задача 2.5. Доказать, что при ![]() :
: ![]() .
.
Решение.
Вычислим производные левой и правой частей: ![]()
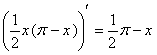
Ясно, что ![]() , поскольку
, поскольку ![]() ,
, ![]() . Так как
. Так как ![]() и
и ![]() непрерывные функции, то, согласно теореме 1, имеет место неравенство
непрерывные функции, то, согласно теореме 1, имеет место неравенство
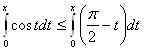 , т.е.
, т.е. ![]() ,
, ![]() . Задача 2.5. решена.
. Задача 2.5. решена.
Теорема 1 позволяет устанавливать истинность нестрогих неравенств. Утверждение, содержащееся в ней, можно усилить, если потребовать выполнения дополнительных условий.
Теорема 2. Пусть выполняются условия теоремы 1 и, кроме того, для некоторого ![]() имеет место строгое неравенство
имеет место строгое неравенство ![]() . Тогда при
. Тогда при ![]() также имеет место строгое неравенство
также имеет место строгое неравенство  .
.
Задача 2.6. Доказать, что при ![]() :
: ![]() (2.8).
(2.8).
Решение.
Предварительно следует проверить соответствующее неравенство для производных левой и правой частей, т.е. что ![]() , или
, или ![]() . Его справедливость при
. Его справедливость при ![]() можно установить, если применить теорему 1 к неравенству
можно установить, если применить теорему 1 к неравенству ![]() . Поскольку, кроме того,
. Поскольку, кроме того, ![]() , то выполняются все условия теоремы 2. Поэтому имеет место строгое неравенство
, то выполняются все условия теоремы 2. Поэтому имеет место строгое неравенство 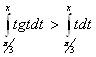 ,
, ![]() , или
, или  ,
, ![]() . После преобразований придем к неравенству (2.8).
. После преобразований придем к неравенству (2.8).
Похожие работы
... сформулированной гипотезы необходимо было решить следующие задачи: 1. Выявить роль тригонометрических уравнений и неравенств при обучении математике; 2. Разработать методику формирования умений решать тригонометрические уравнения и неравенства, направленную на развитие тригонометрических представлений; 3. Экспериментально проверить эффективность разработанной методики. Для решения ...
... точек координатной оси. Занятие № 4. Тема: Аналитический метод. Метод «ветвлений». Цель занятия: познакомить учеников с основным методом решения уравнений, содержащих параметр. Литература для учителя: см. [1] , [5], [6], [7], [14] Литература для ученика: см. [3] Краткое содержание: рассмотрение различных значений, принимаемых параметром. Упрощение уравнения и приведение уравнения к произведению ...
... по алгебре и началам анализа, при подготовке к государственной итоговой аттестации, внешнему независимому оцениванию. Достаточно большое число задач раскрывают потенциальные возможности анализа бесконечно малых величин. 1. Производная и ее применение для решения прикладных задач 1.1 Исторические сведения Ряд задач дифференциального исчисления был решен еще в древности. Они встречались у ...
... выше теорема свидетельствует о важности априорных оценок для доказательства теорем существования и единственности решений. Глава 2. Приложение Пример 1. Рассмотрим интегральное уравнение с малым вещественным параметром λ: (1) Это уравнение вида А()х = у() – операторное уравнение в С[-π; π], где Покажем, что А() аналитична в т. 0, т.е. разлагается в ряд вида . Разложим функцию ...





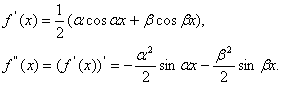

0 комментариев