Навигация
Интегралы от выпуклых функций
33097
знаков
0
таблиц
0
изображений
2.3. Интегралы от выпуклых функций
При решении многих задач целесообразно применять следующий подход.
Разделим отрезок [a,b], на котором задана непрерывная функция f. на n частей точками 
. Построим прямоугольные трапеции, основаниями которых являются отрезки xkyk, xk+1yk+1, а высотами – xkxk+1, k=0,1,…,n-1. Сумма площадей этих трапеций при достаточно большом n близка к площади криволинейной трапеции. Чтобы этот факт можно было применить к доказательству неравенств функция f должна удовлетворять некоторым дополнительным требованиям.
Пусть функция f дважды дифференцируема на некотором промежутке и в каждой точке этого промежутка f//(x)>0. Это означает, что функция f/ возрастает, т.е. при движении вдоль кривой слева направо угол наклона касательной к графику возрастает. Иными словами, касательная поворачивается в направлении, обратном направлению вращения часовой стрелки. График при этом «изгибается вверх», «выпячиваясь вниз». Такая функция называется выпуклой. График выпуклой функции расположен «ниже» своих хорд и «выше» своих касательных. Аналогично, если f//(x)<0, то f/ убывает, касательная вращается по часовой стрелке и график лежит «выше» своих хорд, но «ниже» своих касательных. Такая функция называется вогнутой.
Функция 
вогнута в области своего определения, так как 
. Вторая производная функции 
положительна на всей числовой прямой. Поэтому 
– выпуклая функция. Для функции 
вторая производная 
при 
, 
при 
, т.е. функция на интервале
вогнута, а на 
выпукла.
Задача 2.7. Доказать, что 
Решение.
Левая часть этого неравенства равна площади прямоугольной трапеции, основания которой равны значениям функции в точках 
и 
, т.е. 
и 
, а высота – 
. Функция выпуклая. Поэтому площадь криволинейной трапеции, ограниченной ее графиком, прямыми 
и отрезком [a,b] оси x, меньше площади прямоугольной трапеции. Итак,
.
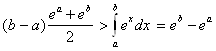Подобный результат имеет место и в общем случае. Пусть функция f на отрезке [a.b] непрерывна, положительна и выпукла. Тогда
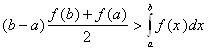(2.9)
Если же непрерывная, положительная функция f вогнута, то
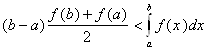(2.10)
Задача 2.8. Доказать, что для 
выполняется неравенство 
Решение.
Функция 
непрерывна, положительна, вогнута. Поэтому для нее выполняется неравенство (2), где 
. Имеем
.
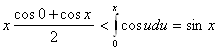График функции f, выпуклой на отрезке [a,b] лежит выше любой касательной к этому графику, в частности касательной, проведенной через точку кривой с абсциссой 
.
Если касательная пересекает ось абсцисс вне отрезка [a,b], то она отсекает от криволинейной трапеции прямоугольную трапецию, а не треугольник. Площадь прямоугольной трапеции равна произведению ее средней линии 
на высоту . Поэтому
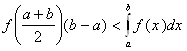(2.11)
аналогично, если функция f вогнута, то
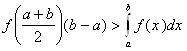(2.12)
Соотношение
остается справедливым если касательная к графику 
пересекает ось абсцисс в точках a и b.
Задача 2.9. Доказать, что если 0<a<b , то выполняется 
.
Решение.
представляет собой площадь криволинейной трапеции, ограниченной линиями 
, т.е. 
. Касательная к кривой 
в точке 
отсекает от криволинейной трапеции прямоугольную трапецию, высота которой , а средняя линия 
. Площадь этой трапеции равна 
. Согласно неравенству (2.6), 
.
Убедимся, что указанная касательная отсекает именно трапецию, а не треугольник. Для этого достаточно проверить что точка ее пересечения с осью абсцисс лежит вне отрезка [a,b]. Уравнение касательной к кривой в точке 
имеет вид 
. В данном случае 
, т.е. 
есть уравнение касательной. Положив в нем 
, найдем абсциссу точки пересечения касательной с осью 
: 
, ч т.д.
Из соотношений (2.9)-(2.12) можно получить новые неравенства. Неравенства (2.9) и (2.11) совместно дают оценку снизу и сверху для интеграла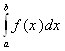 
от непрерывной, положительной и выпуклой функции. Аналогичные оценки получаем для интегралов от вогнутых функций из неравенств (2.10) и (2.12). Вернемся к задаче 2.9. Ее удалось решить, применив неравенство (3) к функции на отрезке [a,b]. Кроме того, в силу неравенства (2.9)
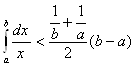, т.е. 
.
Объединяя этот результат с неравенством, доказанным в задаче 2.9, получим двойное неравенство
Похожие работы
... сформулированной гипотезы необходимо было решить следующие задачи: 1. Выявить роль тригонометрических уравнений и неравенств при обучении математике; 2. Разработать методику формирования умений решать тригонометрические уравнения и неравенства, направленную на развитие тригонометрических представлений; 3. Экспериментально проверить эффективность разработанной методики. Для решения ...
... точек координатной оси. Занятие № 4. Тема: Аналитический метод. Метод «ветвлений». Цель занятия: познакомить учеников с основным методом решения уравнений, содержащих параметр. Литература для учителя: см. [1] , [5], [6], [7], [14] Литература для ученика: см. [3] Краткое содержание: рассмотрение различных значений, принимаемых параметром. Упрощение уравнения и приведение уравнения к произведению ...
... по алгебре и началам анализа, при подготовке к государственной итоговой аттестации, внешнему независимому оцениванию. Достаточно большое число задач раскрывают потенциальные возможности анализа бесконечно малых величин. 1. Производная и ее применение для решения прикладных задач 1.1 Исторические сведения Ряд задач дифференциального исчисления был решен еще в древности. Они встречались у ...
... выше теорема свидетельствует о важности априорных оценок для доказательства теорем существования и единственности решений. Глава 2. Приложение Пример 1. Рассмотрим интегральное уравнение с малым вещественным параметром λ: (1) Это уравнение вида А()х = у() – операторное уравнение в С[-π; π], где Покажем, что А() аналитична в т. 0, т.е. разлагается в ряд вида . Разложим функцию ...
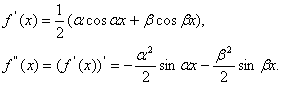
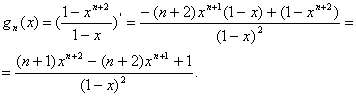
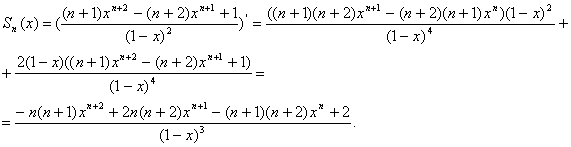
0 комментариев