Навигация
Некоторые классические неравенства и их применение
33097
знаков
0
таблиц
0
изображений
2.4. Некоторые классические неравенства и их применение
Приведем вывод некоторых замечательных неравенств с помощью интегрального исчисления. Эти неравенства широко используются в математике, в том числе и при решении элементарных задач.
Пусть y=f(x) – непрерывная возрастающая при x>0 функция. Кроме того, f(0)=0, f(a)=b, где a, b некоторые положительные действительные числа. Из школьного курса математики известно, что если функция f возрастает и непрерывна на некотором промежутке, то существует функция f-1, обратная функции f. Ее область определения совпадает с множеством значений f. функция f-1 непрерывна и возрастает в области своего определения.
Отсюда следует, что для данной функции f существует непрерывная возрастающая обратная функция f-1 такая, что f-1(0)=0, f-1(b)=a. Графики зависимостей y=f(x) и x=f-1(y) совпадают.
Площадь S1 криволинейной трапеции, ограниченной линиями y=f(x), y=0, x=0, x=a, равна
.
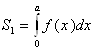Площадь S2 криволинейной трапеции, ограниченной линиями x=f-1(y), x=0, y=0, y=b, равна 
В последнем равенстве мы переобозначили переменную интегрирования, что, конечно, несущественно при вычислении интеграла. Поскольку площадь прямоугольника равна сумме площадей S1 и S2, то
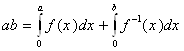
Может оказаться, что f(a) не равно заданному числу b, т.е. f(a)>b или f(a)<b.
В каждом из этих случаев площадь прямоугольника меньше суммы площадей криволинейных трапеций, равной S1+S2.
Объединяя эти три случая, получаем следующий результат.
Пусть f и f-1 – две непрерывные возрастающие взаимно обратные функции, обращающиеся в нуль в начале координат. Тогда для a>0, b>0 имеет место неравенство
(2.13)
Равенство имеет место тогда и только тогда, когда b=f(a). Это неравенство называют неравенством Юнга. Оно является источником получения других важных неравенств.
Пример 2.10. Функция f, где f(x)=x, удовлетворяет условиям, при которых справедливо соотношение (1). Далее.,f-1(x)=x. Поэтому
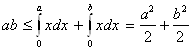(2.14)
Пример 2.11. Функция f, где f(x)=xa, a>0, непрерывна, возрастает при x>0, f(0)=0. Обратной для нее является функция f-1, где f-1(x)=x1/a. Из неравенства (2.13) имеем
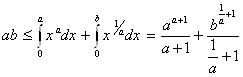. Обозначив 
, получим
(2.15)
Из неравенства (2.15) может быть получено известное неравенство Гельдера:
где
Из неравенства (2.15) может быть выведено и так называемое интегральное неравенство Гельдера:
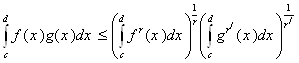
где 
.
Полагая r=2, получим известное неравенства Коши-Буняковского:
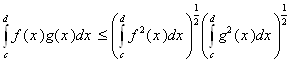
Задача 2.21. Доказать, что для произвольного 
выполняется
Решение.
Неравенство достаточно доказать при 
. Положив в неравенстве 
, имеем
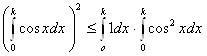
Так как 
, 
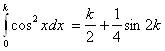, то получаем 
, или 
.
ПЕРЕЧЕНЬ ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Алгебра и начала анализа для 9-10 классов / Под ред. А.Н. Колмогорова. – М.: Просвещение, 1986. – 336с.
2. Бродский Я.С., Слипенко А.К. Производная и интеграл в неравенствах, уравнениях, тождествах. – К., Выща школа, 1988. – 120с.
3. Дороговцев А.Я. Інтеграл та його застосування. – К.: Вища школа. 1974. – 125с.
4. Дорофеев Г.М. Применение производных при решении задач в школьном курсе математики // Математика в школе. – 1980. – №5 – с. 12-21, №6 – с. 24-30.
5. Рижов Ю.М. Похідна та її застосування. – К. Вища школа, 1977. – 83с.
6. Ушаков Р.П., Хацет Б.І. Опуклі функції та нерівності. – К. Вища школа, 1986. – 112с.
7. Шунда Н.М., Томусяк А.А. Практикум з математичного аналізу: Вступ до аналізу. Диференціальне числення. Навч. посібник.– К., Вища школа, 1993.– 375с.
Похожие работы
... сформулированной гипотезы необходимо было решить следующие задачи: 1. Выявить роль тригонометрических уравнений и неравенств при обучении математике; 2. Разработать методику формирования умений решать тригонометрические уравнения и неравенства, направленную на развитие тригонометрических представлений; 3. Экспериментально проверить эффективность разработанной методики. Для решения ...
... точек координатной оси. Занятие № 4. Тема: Аналитический метод. Метод «ветвлений». Цель занятия: познакомить учеников с основным методом решения уравнений, содержащих параметр. Литература для учителя: см. [1] , [5], [6], [7], [14] Литература для ученика: см. [3] Краткое содержание: рассмотрение различных значений, принимаемых параметром. Упрощение уравнения и приведение уравнения к произведению ...
... по алгебре и началам анализа, при подготовке к государственной итоговой аттестации, внешнему независимому оцениванию. Достаточно большое число задач раскрывают потенциальные возможности анализа бесконечно малых величин. 1. Производная и ее применение для решения прикладных задач 1.1 Исторические сведения Ряд задач дифференциального исчисления был решен еще в древности. Они встречались у ...
... выше теорема свидетельствует о важности априорных оценок для доказательства теорем существования и единственности решений. Глава 2. Приложение Пример 1. Рассмотрим интегральное уравнение с малым вещественным параметром λ: (1) Это уравнение вида А()х = у() – операторное уравнение в С[-π; π], где Покажем, что А() аналитична в т. 0, т.е. разлагается в ряд вида . Разложим функцию ...
0 комментариев