Навигация
Фигурные диаграммы – статистические данные изображаются рисунками – символами (не всегда точно отражают данные)
5. Фигурные диаграммы – статистические данные изображаются рисунками – символами (не всегда точно отражают данные).
6. Знаки Варзара (русский статистик) – применял прямоугольные фигуры для графического изображения 3-х показателей, один из которых равен произведению двух других:

Ø 2. Картограмма – схематическая карта, на которой отдельные территории в зависимости от показателей обозначаются с помощью графических символов (штриховки, расцветки, точки).
а) фоновые – различные цвета, штриховка
б) точечные – в качестве графического знака используются точки одинакового размера.
Ø 3. Картодиаграмма – сочетание контурной карты с диаграммой.
Геометрические символы – столбики, круги размещаются по всей карте.
II. В зависимости от формы применения графических образов статистические графики могут быть:
1) точечными – совокупность точек
2) линейными
3) плоскостными – прямоугольники, квадраты
4) фигурными.
III. В зависимости от характера решаемых задач:
1) статистические графики рядов распределения
2) структуры статистической совокупности
3) рядов динамики
4) показателей связи
5) показателей выполнения заданий.
Статистические ряды распределенияРезультаты сводки и группировки материалов статистического наблюдения оформляются в виде статистических рядов распределения.
Статистические ряды распределения представляют собой упорядоченое расположение единиц изучаемой совокупности на группы по группировочному признаку.
Они характеризуют состав (структуру) изучаемого явления, позволяют судить об однородности совокупности, границах ее изменения, закономерностях развития наблюдаемого объекта.
Ряды распределения, образованные по качественным признакам, называются атрибутивными.
При группировке ряда по количественному признаку получаются вариационные ряды (дискретные, интервальные).
Вариационные ряды состоят из 3‑х элементов:
1) варианты – отдельного значения варьируемого признака, которое он принимает в ряду распределения.
2) частоты – численности отдельных вариант или каждой группы вариационного ряда.
3) частости – частот, выраженных в долях единицы или в процентах к итогу.
Сумма частот составляет объем ряда распределения.
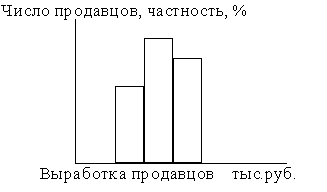
Интервальный ряд распределения изображается графически в виде гистограммы. На оси «х»- отображаются интервалы ряда, высота которых равна частотам, отложенным на оси «у».
Гистограмма
Кумулята распределения
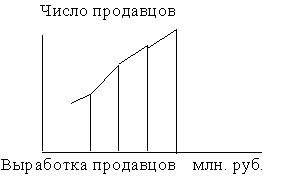
Накопленные частоты в основе графика в виде кумуляты называются кривой сумм. Это кривые концентрации называются кривыми Лоренца.
5. Относительные и средние величины
Абсолютные величины.
Обобщающие показатели – это полученные в результате статистической сводки и выраженные в таблицах статистические данные, характеризующие совокупность в целом или отдельные ее части.
Абсолютные обобщающие величины получают в результате сводки путем суммирования первичного статистического материала или расчетов на основе других показателей (приросты, вторичные показатели).
По способу выражения размеров изучаемых явлений абсолютные величины подразделяются на индивидуальные и суммарные.
Индивидуальные – характеризуют размеры количественных признаков у отдельных единиц наблюдения.
Абсолютные показатели всегда являются именованными числами, т.е. имеют определенную размерность. Единицы измерения бывают:
1) натуральные – соответствуют природным или потребительским свойствам предмета. Могут быть простыми – кг, т, км, сложными – чел.-час.
2) денежные – стоимостные (руб., млн. руб.)
3) трудовые единицы измерения – чел.-день
4) условные натуральные единицы – служат для сопоставимости. Например, в сельском хозяйстве – усл. га пашни, усл. поголовье.
Относительные величины – качественная оценка экономических явлений, рассчитываются как частное от деления двух статистических величин и характеризуют количественное соотношение между ними. В числителе – показатель изучаемого явления, в знаменателе – показатель, с которым производится сравнение, т.е. база сравнения.Вычисления производят в долях или процентах.
Основание сравнения – 100 – в %, 1000 – в промилле, 10000 – в децимилле.
По своему познавательному значению относительные величины подразделяются на следующие виды:
I. Результат сопоставления одноименных статистических показателей –
Направления сопоставления:
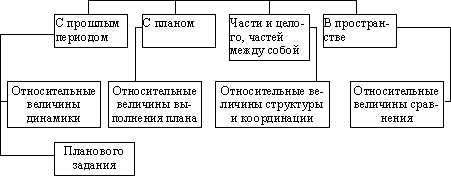
II. Результат сопоставления разноименных статистических показателей:
1) Показатель выполнения плана соответствует фактическому выполнению плана.
2) Относительные величины структуры – характеризуют состав изучаемых совокупностей.
Исчисляются они как отношение абсолютной величины каждого из элементов совокупности к абсолютной величине всей совокупности, т.е. как отношение части к целому и представляют собой удельный вес части в целом.
![]()
3) Относительные величины динамики – характеризуют изменение изучаемого явления во времени, определяют направление развития, измеряют интенсивность развития. Рассчитываются в виде темпов роста и других показателей динамики.
4) Относительные величины сравнения – характеризуют количественное соотношение одноименных показателей, относящихся к различным объектам наблюдения.
5) Относительные величины координации – разновидность показателей сравнения. Применяются для характеристики соотношения между отдельными частями статистической совокупности и показывают, во сколько раз сравниваемая часть совокупности больше или меньше части, которая принимается за основание сравнения, т.е. характеризует структуру изучаемой совокупности.
6) Относительные величины интенсивности – показывают, насколько широко распространено изучаемое явление в среде. Они характеризуют соотношение разноименных, но связанных между собой абсолютных величин. Выражаются именованными величинами. Рассчитываются делением абсолютной величины изучаемого явления на абсолютную величину, характеризующую объем среды, в которой происходит развитие явления. Относительная величина показывает, сколько единиц одной совокупности приходится на единицу другой совокупности.
Обобщающие статистические показатели отражают количественную сторону изучаемой совокупности общественных явлений, т.е. представляют собой их величину, выраженную соответствующими единицами измерения.
Статистические показатели имеют взаимосвязанные количественную и качественную стороны. Качественная сторона показателя – его содержание. Количественная сторона – числовое значение.
Средние величины
Теория средних величин занимает одно из центральных мест в общей теории статистики. Средние величины широко применяются не только в статистике, но и во многих других науках, в управленческой деятельности, научно-исследовательской работе.
Под средней величиной понимается обобщенная количественная характеристика признака в статистической совокупности. Средняя выражает величину признака, отнесенную к единице совокупности и абстрагированную от индивидуальных особенностей отдельных единиц.
Благодаря этой абстракции создаются предпосылки для выявления характерных, типичных размеров признака в совокупностях, для изучения свойств и закономерностей массовых общественных явлений в конкретных условиях места и времени.
В средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами. В средних величинах находят выражение общие, закономерные черты, свойственные всей совокупности явления. Это свойство средних предопределяет использование их в качестве основного метода статистической науки.
Итак, средние величины – это обобщающие показатели, в которых находят выражение действие общих условий, закономерность изучаемого явления. Статистическая средняя будет объективна и типична, если она рассчитывается по массовым данным для качественно однородной совокупности (массовых явлений). Средняя отражает то общее, что складывается в каждом отдельном, единичном объекте. Благодаря этому средняя получает большое значение для выявления закономерностей, присущих массовым явлениям и не заметных в единичных явлениях. Отклонение индивидуального от общего – проявление процесса развития.
Каждая из конкретных средних выражает определенное свойство совокупности, описанное функцией f (х1, х2…, х n), раскрытие которой приводит к установлению различных видов средних величин.
ü Средняя арифметическая – наиболее распространенный вид средней. Она исчисляется в тех случаях, когда объем осредняемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности.
1) арифметическая простая рассчитывается, когда дан ряд одиночных значений признака
2) арифметическая взвешенная рассчитывается при определении среднего значения признака по ряду распределения, когда одно и то же значение признака встречается несколько раз.
Для исчисления проводится умножение каждого варианта на его частоту, суммирование полученных произведений и деление полученной суммы на сумму частот.
ü Средняя гармоническая – это величина, обратная средней арифметической, когда k = – 1 (по схеме в ПТК.)
Когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение, применяется формула средней гармонической взвешенной.
ü Средняя геометрическая – это величина, используемая как средняя из отношений или в рядах распределения, представленная в виде геометрической прогрессии. Этой средней удобно пользоваться, когда уделяется внимание не абсолютным разностям, а отношением двух чисел. Средняя геометрическая используется а расчетах среднегодовых темпов роста.
Мода – чаще всего встречающийся вариант, или значение признака, который соответствует максимальной точке теоретической кривой распределения.
1). Для дискретных рядов – вариант, имеющий наибольшую частоту.
2). В интервальном вариационном ряду – модальный интервал определяется по наибольшей частоте или по наибольшей плотности распределения.
Во многих случаях при характеристике совокупности в качестве
обобщенного показателя отдается предпочтение моде, а не средней арифметической:
1) при изучении цен на рынках фиксируется и изучается в динамике не средняя цена на определенную продукцию, а модальная;
2) при изучении спроса населения на определенный размер обуви или одежды представляет интерес определение модального номера;
3) при характеристике типичности: если средняя арифметическая близка по значению к моде, значит она типична.
Медиана – значение признака у средней единицы ранжированного ряда (т.е. ряда, у которого значения признака записаны в порядке возрастания или убывания). Рассчитывается:
1) для ранжированного ряда с нечетным числом членов медианой является варианта, расположенная в центре ряда; 2) с четным числом членов – средняя арифметическая из двух смежных вариант.
В интервальном вариационном ряду:
1) ранжируем индивидуальные значения признака;
2) определяем для ряда накопленные частоты;
3) по данным о накопленных частотах находим медианный интервал.
Похожие работы
... его увеличением для целей информационного обеспечения исполнительных местных органов [7,8]. 3 ОПЫТ УПРАВЛЕНИЯ И ОБОЩЕНИЕ ДАННЫХ НА ПРИМЕРЕ АЛМАТИНСКОГО ОБЛАСТНОГО УПРАВЛЕНИЯ СТАТИСТИКИ3.1 Алматинское областное управление статистики как субъект сбора и обобщения статистической информации В своей деятельности Алматинское областное управление статистики (АОУС) руководствуется ...
... и раскрыто содержание основных бухгалтерских отчетов. Также приведена краткая характеристика аудиторского заключения, цель которого - дать независимое объективное суждение подтверждающее достоверность бухгалтерской отчетности организации, если она в соответствии с федеральными законами подлежит обязательному аудиту. Затем были рассмотрены и приведены примеры и схемы взаимосвязей форм отчетности. ...
... месте. Для понимания содержащейся в нем информации важно иметь представление не только о структуре бухгалтерского баланса, но и знать основные логические и специфические взаимосвязи между отдельными показателями. Не менее существенное значение в понимании содержания бухгалтерского баланса имеет последовательность его чтения, а также непременное знание отдельных ограничений, присущих только ...
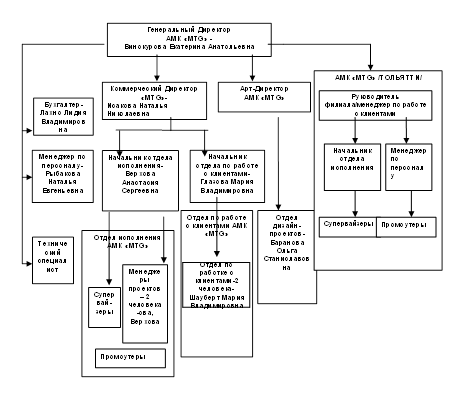
... связи с Администрациями года и области; Ø - опыт организации и проведения уникальных мероприятий. 1.3. Структура компании АМК «MTG». На приведённой схеме изображена организационная структура компании Агентство маркетинговых коммуникаций «MTG». 1.4 Описание каждого отдела ООО «MTG». Определение типа организационной структуры Генеральный директор Генеральный директор ...
0 комментариев