С помощью регрессии определяется форма связи и оцениваются параметры регрессии

1. С помощью регрессии определяется форма связи и оцениваются параметры регрессии.

2. Посредством корреляционного анализа определяется сила связи между факторами.

Значит, можно численно охарактеризовать как интенсивность и направление связей, так и степень влияния различных факторов.

Результаты анализа приобретают количественное выражение: 1) в уравнениях, описывающих форму связи и 2) коэффициентах регрессии.

Кроме изменчивости оцениваются и степень интенсивности корреляции между результативным фактором y и влияющим на него производственными факторами x_j.

Степень интенсивности корреляции определяется коэффициентом множественной корреляции R_yxj

Пример: R=0,803 – по шкале Чеддока определяется – высокая степень связи. Для проверки надежности установления коэффициентов множественной корреляции необходимо найти значение критерия Фишера, сравнить с табличным значением при доверительном уровне вероятности суждения и соответствующем числе степеней свободы.

,

R² – квадрат коэффициента корреляции или коэффициент множественной детерминации;

n – численность выборочной совокупности;

m – число параметров в уравнении связи, включая и параметр a₀.

Если F_факт.>F_табл., значит, зависимость результативного y от факторов описывается уравнением достоверно и существенно.

Оценка существенности коэффициентов множественной корреляции при определенной вероятности ошибки (0,05) и числе свободы k – по таблицам определяются критические значения t‑Стьюдента.

t_факт.>t_крит. – связь надежна

 – утроенная среднеквадратическая ошибка коэффициента корреляции не превышает их расчетного значения – связь надежна.

Измерить надежное влияние, которое оказывают вариации всех исследуемых факторов, позволяет квадрат множественного коэффициента корреляции – называется коэффициентом множественной детерминации D=R². Если R=0,803, то D=R²=0,645. И это означает, что 64,5% общей вариации объясняется изменением изучаемых факторов x_j. R=0,925D=85,4%

Возможность определить долю, вносимую каждым фактором в модификацию уровня результативного показателя, дает коэффициент частной детерминации: .

Степень влияния каждого фактора, включенного в вычисление корреляции, выражается той частью дисперсии значений признака явлений, которая определяется вариацией значений соответствующего фактора.

Сумма d_j=D. В нашем примере:

d₁=0,201; d₄=0,005

d₂=0,204; d₅=0,166

d₃=0,039; d₆=0,239

Вывод: Наибольшее влияние оказывают: x6, x2 и x1.

Анализ коэффициентов регрессии

Прямое сравнение коэффициентов регрессии невозможно, так как они не выражены в одинаковых единицах.

а) Применение коэффициентов эластичности .

 – устраняет различие в единицах измерения.

 – показывает, на сколько% изменится результативный признак при изменении факторного признака на 1% при фиксировании значений остальных факторов на каком-либо уровне. Если в качестве такого уровня принять их средние значения, то получим средний коэффициент эластичности :

₁=0,420; ₃=0,038; ₅=0,164

₂=0,827; ₄=0,024; ₆=0,754.

Вывод: Сравнением легко установить, что самое значительное влияние на результативный признак оказывают производственные факторы x₂, x₆ и x₁.

б)  – коэффициенты – нормированные коэффициенты регрессии

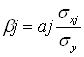, где

a_j – коэффициент регрессии при факторе xj;

 – среднее квадратическое отклонение факторного признака x_j;

 – среднее квадратическое отклонение результативного признака y.

Интерпретация : Чтобы установить, в развитии каких факторов заложены возможности изменения y, следует учесть степень колеблемости факторов, которая характеризуется среднеквадратическим отклонением и коэффициентом вариации (v_x)/

1=0,223; 3=-0,030; 5=0,214;

2=0,270; 4=-0,050; 6=0,521.

Вывод: x6, x2, x1.

Коэффициент вариации (v_xj), больше y x6=18.5% v_x2=8,8%, v_x1=14,3%.

в) оценка значимости (существенности) коэффициентов регрессии проверяется по значению t – критерия Стьюдента

Значения x1=3,083; x3=0,363; x5=3,059;

t‑критерия: x2=3,781; x4=0,722; x6=6,051.

Вывод: наиболее значимы: x6, x2, x1.

Испытания параметров уравнения регрессии на их типичность

Применительно к совокупностям, у которых n<30 для определений типичности используется t‑критерий Стьюдента.

Алгоритм:

Вычисляются фактические значения t‑критерия:

а) для параметра a₀

;

б) для параметра a₁

, где

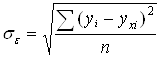 – среднее квадратическое отклонение результативного признака y_i от выравненных значений y_xi;

 – среднее квадратическое отклонение факторного признака x_i от общей средней – .

Полученные по формулам t_a0 и t_a необходимо сравнить с критическими t_k, который находят по таблице Стьюдента с учетом принятого уровня значимости  и числа степеней свободы k.

Похожие работы

Управление процессами организации сбора и обобщения статистических данных на примере Алматинского областного управления статистики

Скачать

168397

13

0

... его увеличением для целей инфор­мационного обеспечения исполнительных местных органов [7,8]. 3 ОПЫТ УПРАВЛЕНИЯ И ОБОЩЕНИЕ ДАННЫХ НА ПРИМЕРЕ АЛМАТИНСКОГО ОБЛАСТНОГО УПРАВЛЕНИЯ СТАТИСТИКИ3.1 Алматинское областное управление статистики как субъект сбора и обобщения статистической информации   В своей деятельности Алматинское областное управление статистики (АОУС) руководствуется ...

Бухгалтерская отчетность организации

Скачать

46943

0

1

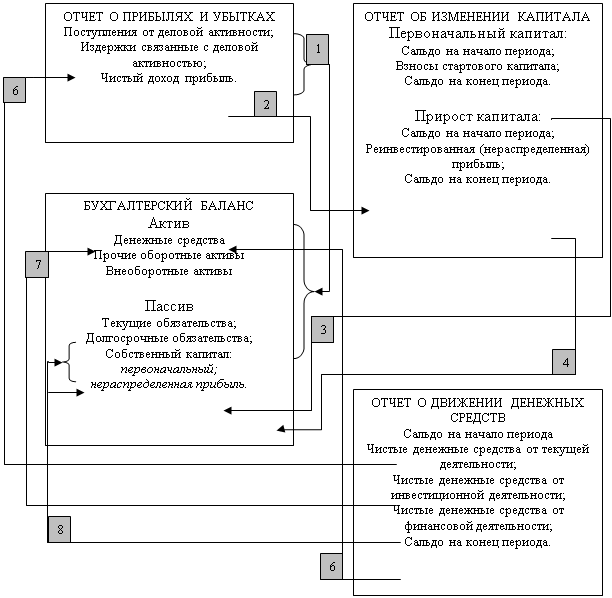
... и раскрыто содержание основных бухгалтерских отчетов. Также приведена краткая характеристика аудиторского заключения, цель которого - дать независимое объективное суждение подтверждающее достоверность бухгалтерской отчетности организации, если она в соответствии с федеральными законами подлежит обязательному аудиту. Затем были рассмотрены и приведены примеры и схемы взаимосвязей форм отчетности. ...

Бухгалтерский баланс, понятие, назначение, порядок составления и структура его статей

Скачать

39359

0

0

... месте. Для понимания содержащейся в нем информации важно иметь представление не только о структуре бухгалтерского баланса, но и знать основные логические и специфические взаимосвязи между отдельными показателями. Не менее существенное значение в понимании содержания бухгалтерского баланса имеет последовательность его чтения, а также непременное знание отдельных ограничений, присущих только ...

Детализированное описание организационной структуры компании

Скачать

29136

1

2

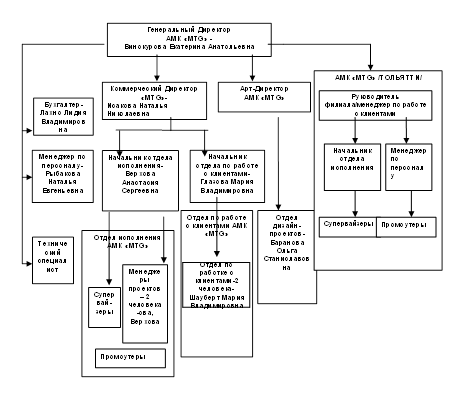
... связи с Администрациями года и области; Ø  - опыт организации и проведения уникальных мероприятий. 1.3.  Структура компании АМК «MTG». На приведённой схеме изображена организационная структура компании Агентство маркетинговых коммуникаций «MTG». 1.4 Описание каждого отдела ООО «MTG». Определение типа организационной структуры Генеральный директор Генеральный директор ...