В векторном пространстве V существуют n линейно независимых векторов

9. В векторном пространстве V существуют n линейно независимых векторов.

10. Любая система, состоящая более, чем из n векторов пространства V, линейно зависима.

Число n называется размерностью векторного пространства и обозначается символом dim V , а само пространство будем обозначать символом V_n. Базисом n-мерного векторного пространства V_n называется любая упорядоченная система векторов, таких, что система линейно независима; любой вектор пространства V_n является линейной комбинацией данной системы векторов. Базис не может иметь более трёх векторов и менее чем три вектора. Очевидно, что базис пространства V₃ будем называть 3-мерным и обозначать В = (е₁, е₂, е₃), где векторы е₁, е₂, е₃ называются базисными. Из аксиом 9 и 10 следует, что в n-мерном векторном пространстве V_n существует хотя бы один базис, состоящий из n векторов. Можно доказать, что в V_n существует бесчисленное множество базисов и любой из них состоит из n векторов. N-мерный базис будем обозначать В = (е₁, е₂,…, е_n), а векторы е₁, е₂,…, е_n называть базисными. Следствие: Любая система, состоящая более чем из трёх векторов обычного пространства трёх измерений, линейно зависима.

 

§ 3. Евклидово векторное пространство

Строя аксиоматическую теорию аналитической геометрии на векторной основе, введём следующее определение.

Определение 1: Скалярным произведением на векторном пространстве V называется операция, которая любой паре векторов a и b ставит в соответствие некоторое действительное число, обозначаем символом a b и обладающее следующими свойствами:11. Для любых векторов a, b V и любого вектора a b= b а;12. Для любых двух векторов a, b V и любого числа .13. Для любых трёх векторов a, b, c V ;14. Для любого ненулевого вектора а V aa>0.

Определение 2: Векторное пространство V_n, в котором введена операция скалярного произведения векторов, удовлетворяющая аксиомам 11-14, называется евклидовым векторным пространством. Будем обозначать его символом Е_n.

На основе определения 1 можно ввести понятие длины вектора и величины угла между векторами.

Число аа называется скалярным квадратом вектора а и обозначается а². Из аксиомы 14 следует, что а²>0, следовательно,  - действительное положительное число. Оно называется длиной или нормой вектора и обозначается: . Если 1, то вектор а называется единичным.

На основе аксиом 11-14 можно указать следующие утверждения: Для любых векторов a, b₁, b₂,…, b_n выполняется равенство

.

 , где а – произвольный вектор;

Если , то , а если , то ;Если , то .

Можно показать, что если , то вектор 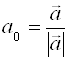 является единичным, его называют ортом вектора а. Он определяет то же направление, что и вектор а.

При решении метрических задач, т. е. задач, связанных с измерением длин векторов и величин углов, пользуются ортонормированным базисом.

Определение: Базис называется ортонормированным, если все его векторы единичные и попарно ортогональны, т. е. если  и  () при .

Теорема. В евклидовом пространстве Е_n существуют ортонормированные базисы.

Действительно, если (а₁, а₂,…, а_n) – ортогональный базис, то можно рассмотреть векторы

, ,…, .

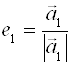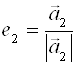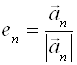Ясно, что базис (е₁, е₂,…, е_n) ортонормированный, так как его векторы единичные и попарно ортогональны.

Введём обозначения: В=(i, j) или B=(i, j, k) – ортонормированные базисы евклидовых векторных пространств Е₂ и Е₃ соответственно.

  § 4. Понятие точечно-векторного аффинного n-мерного пространства

В § 2 и § 3 были аксиоматически определены различные векторные пространства: линейные векторные, n-мерные векторные, евклидовы векторные. Но для построения геометрии, то есть для рассмотрения различных геометрических фигур, одних векторов недостаточно, нужны ещё точки.

Аксиоматизируя построение вектора по двум точкам, введём следующее определение.

Определение. Аффинным пространством называют некоторое множество А^* элементов произвольной природы, называемых точками, для которого задано

а) некоторое векторное пространство V;

б) отображение, которое любым двум точкам А и ВА^* ставит в соответствие некоторый вектор из V, обозначаемый АВ.

При этом требуется выполнение следующих аксиом:

15. Для любой точки АА^* и любого вектора А из V существует единственная точка ВА^* и любого вектора аV существует единственная точка ВА^*, такая что АВ=а.

16. Для любых трёх точек А, В, СA^* имеет место равенство АВ+ВС=АС.

Аксиома 15 называется аксиомой откладывания вектора от точки, а аксиома 16 – аксиомой треугольника, из которой следует правило треугольника и правило параллелограмма сложения векторов.

Размерность пространства V называется размерностью соответствующего аффинного пространства А^* и обозначается символом А^*_n.

Отметим некоторые важные следствия из аксиом 15-16.

При любом выборе точки А вектор АА нулевой.

Если АВ=0, то точки А и В совпадают.

Для любых точек А и В АВ = - ВА.

Если АВ=СD, то АС=ВD.

Для произвольных точек А₁, А₂,…, А_n выполняется равенство А₁А₂+ А₂А₃+ А_n-1А_n= А₁А_n (правило многоугольника сложения векторов).

Пространство А^*_n содержит бесчисленное множество точек.На основе аксиом 1-10 и 15-16 аффинной геометрии нельзя ввести понятий длин отрезков и величин (мер) углов. Эти понятия можно ввести, используя скалярное произведение векторов.

Как известно, введение в V_n скалярного произведения векторов приводит к евклидову векторному пространству Е_n.

Определение. Аффинное пространство А_n^*, в котором соответствующее ему векторное пространство V_n превращено в евклидово векторное пространство Е_n, называется евклидовым n-мерным пространством.

Для этого пространства введём обозначение Е_n. Согласно определению ясно, что всякое аффинное пространство А_n^* можно превратить в евклидово пространство Е_n, задавая на векторном пространстве V_n скалярное произведение векторов, удовлетворяющее аксиомам 11-14 (§ 3).

Таким образом, в Е_n выполняются аксиомы 1-16.

На основе аксиом евклидова пространства строится евклидова геометрия.

В евклидовой геометрии, очевидно, справедлива вся изложенная выше теория аффинной геометрии. Но пространство Е_n обладает метрическими свойствами, которые следуют из аксиом скалярного произведения векторов и связаны с измерением длин отрезков и мер углов. Поэтому евклидову геометрию называют ещё метрической геометрией.

Метрические аксиомы позволяют установить метрику евклидова пространства, т. е. расстояния между его точками. Определим сначала модуль |a| вектора а как неотрицательный корень из его квадрата, т. е.

 (4.1)

Векторы, модуль которых равен 1, будем называть единичными векторами; единичный вектор  будем обозначать а⁰.

Будем считать расстоянием между точками А и В модуль вектора АВ; будем обозначать это расстоянием АВ.

Таким образом, расстояние АВ между точками А(х) и В(y) определяется соотношением

 (4.2)

Из определения расстояния следует, что

Расстояние симметрично, т. е.

АВ=ВА (4.3)

Расстояние позитивно, т. е. (4.4) AB ≥ 0, причём знак равно имеет место только при совпадении точек А и В.Покажем, что для расстояний между точками евклидова пространства помимо свойств 1 и 2 выполняется также «неравенство треугольника».расстояние между всякими двумя точками не более суммы расстояний между этими точками и третьей точкой, т. е.

АС ≤ АВ + ВС (4.5)

Множество точек, для всяких двух точек А и В которого определено число АВ, удовлетворяющего условиям 1-3, называется метрическим пространством. Для доказательства неравенства треугольника докажем так называемое неравенство Коши

  (4.6)

Скалярный квадрат вектора a – tb неотрицателен при любом вещественном t

 

, т. е. .

В случае b = 0 обе части неравенства (4.6) равны 0, т. е. неравенство выполняется автоматически.

Если , получим .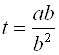

Тогда неравенство примет вид

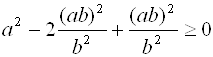, т. е. ,

что равносильно неравенству (4.6). Рассмотрим три точки А(х), В(у) и С(z). Тогда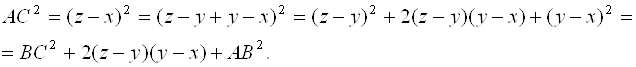

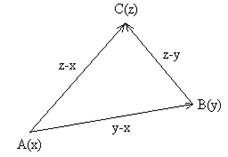Рис. 1

Но в силу неравенства Коши . Поэтому , откуда получаем неравенство (4.5).

Глава II. Многомерные геометрические образы в n-мерных пространствах

  § 5. Четырёхмерное пространство. Определение и его исследование

При построении геометрии на прямой, на плоскости и в трёхмерном пространстве есть две возможности: либо излагать материал с помощью наглядных представлений (этот способ характерен для школьного курса, поэтому трудно себе представить учебник геометрии без чертежей), либо – и эту возможность даёт нам метод координат – излагать его чисто аналитически, назвав, например, точкой плоскости в курсе планиметрии пару чисел (координаты этой точки), а точкой пространства – тройку чисел.При введении четырёхмерного пространства первая возможность у нас отсутствует. Мы не можем непосредственно пользоваться наглядными геометрическими представлениями – ведь окружающее нас пространство имеет всего три измерения. Однако вторая версия для нас не закрыта. В самом деле, мы определяем точку прямой как число, точку плоскости как пару чисел, точку трёхмерного пространства как тройку чисел. Поэтому совершенно естественно построить геометрию четырёхмерного пространства, определив точку этого воображаемого пространства как четвёрку чисел. Под геометрическими фигурами в таком пространстве нужно будет понимать некоторые множества точек (как, впрочем, и в случае обычной геометрии). Перейдём теперь к точным определениям.

Координатные оси и плоскости

Определение. Точкой четырёхмерного пространства называется упорядоченная четвёрка чисел (x, y, z, t).

Что считать в пространстве четырёх измерений координатными осями и сколько их?

Чтобы ответить на этот вопрос, вернёмся на время к плоскости и трёхмерному пространству.

На плоскости (т. е. в пространстве двух измерений) координатные оси – это множества точек, у которых одна из координат может иметь одно числовое значение, а вторая равна нулю. Так, ось абсцисс – это множество точек вида (х, 0), где х – любое число. Например, на оси абсцисс лежат точки (1, 0), (-3, 0), а точка (1/5, 2) не лежит на оси абсцисс.

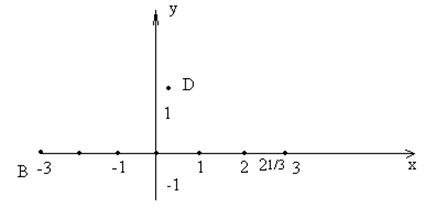Рис. 2

Ось ординат плоскости – это множество точек вида (0, у), где у – любое число. В трёхмерном пространстве есть три оси: ось х – это множество точек вида (х, 0, 0), где х – любое число; ось у – множество точек вида (0, у, 0), где у – любое число; ось z – множество точек вида (0, 0, z), где z – любое число.В четырёхмерном пространстве, состоящем из всех точек вида (x, y, z, t), где x, y, z, t – любые числа, естественно считать координатными осями такие множества точек, у которых одна из координат принимает любые числовые значения, а остальные равны нулю. Тогда ясно, что в четырёхмерном пространстве есть четыре координатные оси: ось х – это множество точек вида (х, 0, 0, 0), где х – любое число; ось у – множество точек вида (0, у, 0, 0), где у – любое число; ось z – множество точек вида (0, 0, z, 0), где z – любое число, где у – любое число; ось t – множество точек вида (0, 0, 0, t), где t – любое число. В трёхмерном пространстве, кроме координатных осей, имеются ещё координатные плоскости. Это – плоскости, проходящие через две какие-либо две координатные оси. Например, плоскость yz – это плоскость, проходящая через ось y и ось z.

Всего в трёхмерном пространстве есть три координатные плоскости:

плоскость xy – множество точек вида (х, у, 0), где х и у – любые числа;

плоскость yz – множество точек вида (х, 0, z), где х и z – любые числа;

плоскость yz – множество точек вида (0, у, z), где y и z – любые числа.

Естественно, и в четырёхмерном пространстве называть координатными плоскостями множество точек, у которых какие-либо две из четырёх координат принимают любые числовые значения, а остальные две равны нулю. Например, множество точек вида (x, 0, z, 0) мы будем называть координатной плоскостью xz четырёхмерного пространства. Сколько же всего таких плоскостей?

Выпишем их:

плоскость ху – множество точек, вида (х, у, 0, 0),

плоскость хz – множество точек, вида (х, 0, z, 0),

плоскость хt – множество точек, вида (х, 0, 0, t),

плоскость уz – множество точек, вида (0, у, z, 0),

плоскость уt – множество точек, вида (0, у, 0, t),

плоскость zt – множество точек, вида (0, 0, z, t).

Для каждой из этих плоскостей переменные координаты могут принимать любые числовые значения, в том числе и нулевое. Например, точка (5, 0, 0, 0) принадлежит плоскости xy и плоскости xt. Тогда легко видеть, что, например, плоскость yz «проходит» через ось у в том смысле, что каждая точка этой оси принадлежит этой плоскости. Действительно, любая точка на оси у, т. е. точка вида (0, у, 0, 0), принадлежит множеству точек вида (0, y, z, 0), т. е. плоскости yz.

Итак, в четырёхмерном пространстве существуют множества точек, аналогичные координатным плоскостям трёхмерного пространства. Их шесть. Каждое из них состоит из точек, у которых, как и у точек координатных плоскостей трёхмерного пространства, две какие-либо координаты могут принимать любые числовые значения, а остальные две равны нулю. Каждая из этих координатных плоскостей «проходит» через две координатные оси: например, плоскость yz проходит через ось у и ось z. С другой стороны, через каждую ось проходят три координатные плоскости. Так, через ось х проходят плоскости xy, xz, xt. Будем говорить, что ось х является пересечением этих плоскостей. Все шесть координатных плоскостей содержат одну общую точку. Это точка (0, 0, 0, 0) – начало координат.

Получаем аналогичную тому, что имеется в трёхмерном пространстве. Представим схематический рисунок, который поможет создать некоторый наглядный образ расположения координатных плоскостей и осей четырёхмерного пространства.

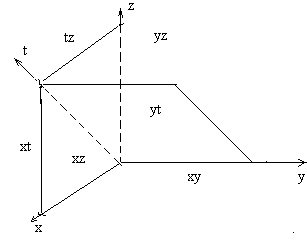
Рис. 3

На рисунке оси координат изображены прямыми, показаны координатные плоскости, все точно также, как и для трёхмерного пространства.

Однако, в четырёхмерном пространстве есть ещё множества точек, которые можно называть координатными плоскостями. На прямой имеется только начало координат, на плоскости есть и начало координат, и оси в трёхмерном пространстве, кроме начала и осей, появляются ещё и координатные плоскости. Естественно, что в четырёхмерном пространстве появляются новые множества, которые будем называть трёхмерными координатными плоскостями.

Это – множества, состоящие из всех точек, у которых какие-либо три из четырёх координат принимают всевозможные числовые значения, а четвёртая равна нулю.

Таково, например, множество, имеющее вид (х, 0, z, t), где x, z, t принимают всевозможные значения. Это множество будем называть трёхмерной координатной плоскостью xzt. Легко понять, что в четырёхмерном пространстве существует четыре координатные трёхмерные плоскости:

плоскость xyz – множество точек вида (x, y, z, 0),

плоскость xyt - множество точек вида (x, y, 0, t),

плоскость xzt - множество точек вида (x, 0, z, t),

плоскость yzt - множество точек вида (0, y, z, t).

Каждая из трёхмерных координатных плоскостей «проходит» через начало координат и что каждая из этих плоскостей «проходит» через три координатные оси (слово «проходит» мы здесь употребляем в том смысле, что начало координат и каждая из точек осей принадлежат плоскости). Например, трёхмерная плоскость xyt проходит через оси x, y, t.

Аналогично, можно сказать, что каждая из двумерных плоскостей является пересечением двух трёхмерных плоскостей.

Например, плоскость ху является пересечением трёхмерных плоскостей xyz и xyt, т. е. состоит из всех точек, принадлежащих одновременно и тому и другому множеству.

Четырёхмерный куб

Определение сферы и куба

Перейдём теперь к рассмотрению геометрических фигур в четырёхмерном пространстве. Под геометрической фигурой (как и в случае обычной геометрии) будем понимать некоторое множество точек.

Возьмем, например, определение сферы: сфера есть множество точек, удалённых от некоторой точки на одно и то же расстояние.

Это определение уже можно использовать, чтобы по аналогии определить сферу в четырёхмерном пространстве: что такое точка, мы знаем; что такое расстояние между точками, тоже знаем. Мы и примем определение, переведя его на язык чисел (для простоты, как и в случае трёхмерного пространства, возьмём сферу с центром в начале координат).

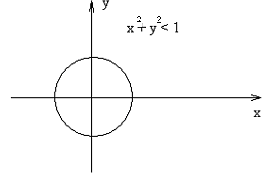
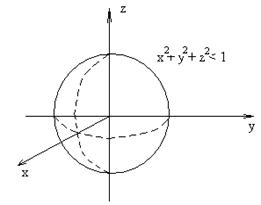
2-мерный шар (круг) 3-мерный шар

рис. 4

 

Определение. Множество точек (x, y, z, t), удовлетворяющих соотношению

 (5. 1)

называется четырёхмерной сферой с центром в начале координат и радиусом R.

Если рассматривать не сферу, а шар, то указанное равенство надо заменить неравенством

 (5. 2)

Это замечание относится также к двумерному и к трёхмерному случаям.

Расскажем теперь немного о четырёхмерном кубе. Судя по названию, его фигура, аналогичная обыкновенному, хорошо знакомому трёхмерному кубу.

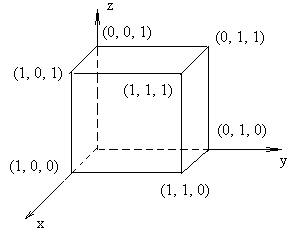
3-мерный куб

Рис. 5

На плоскости тоже есть фигура, аналогичная кубу, - это квадрат.

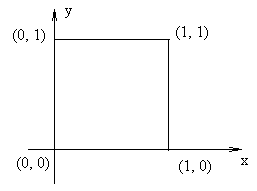
2-мерный куб (квадрат)

Рис. 6

Кубом называется множество точек (x, y, z), удовлетворяющих соотношениям:

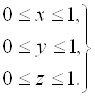 (5. 3)

Это «арифметическое» определение куба не нуждается ни в каком чертеже. Однако оно полностью соответствует геометрическому определению куба.

В пространстве есть и другие кубы. Например, множество точек, определяемых соотношениями    тоже является кубом. Этот куб хорошо расположен относительно координатных осей: начало координат является его центром, координатные оси и координатные плоскости – осями и плоскостями симметрии. Однако для наших целей удобен именно куб, определяемый соотношениями (5. 3). Такой куб мы будем иногда называть единичным, чтобы отличить его от других кубов.

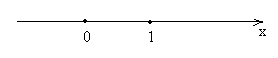
одномерный куб (отрезок)

рис. 7

Для квадрата тоже можно дать арифметическое определение: квадратом называется множество точек (х, у), удовлетворяющих соотношениям:

Сравнивая эти два определения, легко понять, что квадрат действительно является, как говорят, двумерным аналогом куба. Будем называть иногда квадрат «двумерным кубом».

Можно также рассмотреть аналог этих фигур и в пространстве одного измерения – на прямой. Получим множество точек х прямой, удовлетворяющих соотношениям:

Ясно, что таким «одномерным кубом» является отрезок.

Определение. Четырёхмерным кубом называется множество точек (x, y, z, t), удовлетворяющих соотношениям

 

Устройство четырёхмерного куба

Рассмотрим по порядку «кубы» различных размерностей, т. е. отрезок, квадрат и обычный куб.

Отрезок, определяемый соотношениями  является очень простой фигурой. Про него можно сказать, что его граница состоит из двух точек: 0 и 1. Остальные точки отрезка будем называть внутренними.

Граница квадрата состоит из четырёх точек (вершин) и четырёх отрезков. Таким образом, квадрат имеет на границе элементы двух типов: точки и отрезки. Граница трёхмерного куба содержит элементы трёх типов: вершины – их 8, рёбра (отрезки) – их 12 и границ (квадраты) – их 6.

Запишем эти данные в виде таблицы:

Состав границы Фигура	Точек  (вершин)	Отрезок  (сторон, рёбер)	Квадратов (граней)
Отрезок	2	-	-
Квадрат	4	4	-
Куб	8	12	6

Эту таблицу можно переписать короче, если условиться писать вместо названия фигуры число n, равное её размерности: для отрезка n = 1; для квадрата n = 2; для куба n = 3. Вместо названия элемента границы тоже можно писать размерность этого элемента: для грани n = 2, для ребра n = 1.

При этом точку (вершину) удобно считать элементом нулевой размерности (n = 0). Тогда предыдущая таблица примет следующий вид:

размерность  границы размерность куба	0	1	2
1	2	-	-
2	4	4	-
3	8	12	6
4	16	32	24

Цель – заполнить четвёртую строку этой таблицы.

Граница отрезка  состоит из двух точек: х = 0 и х =1. Граница квадрата   содержит 4 вершины:

 

х = 0, у = 0; х = 0, у = 1; х = 0, у = 1; х = 1, у = 1, т. е. точки (0, 0), (0, 1), (1, 0), (1, 1).

Куб  , , содержит восемь вершин. Каждая из этих вершин есть точка (x, y, z), в которой x, y, z заменяются либо нулём, либо единицей. Получаем следующие 8 точек:

(0, 0, 0), (0, 0, 1), (0, 1, 0), (1, 0, 0), (0, 1, 1), (1, 1, 0), (1, 0, 1), (1, 1, 1).

Вершинами четырёхмерного куба:  , ,  называются точки (x, y, z, t), у которых x, y, z, t заменяются либо нулём, либо единицей. Таких вершин 16.

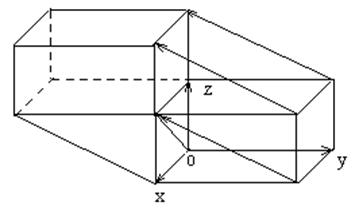
Рис. 8

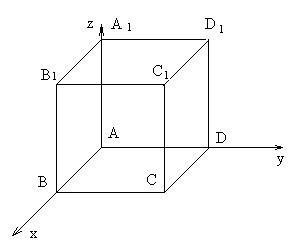Тогда рёбрами (трёхмерного) куба являются стороны.

 

 Рис. 9

х = 0, у = 0,  (ребро АА₁)

, у = 0, z = 1 (ребро АB₁)

 

х = 1, , z = 1 (ребро B₁А₁) и т. д.

Определение. Рёбрами четырёхмерного куба называется множество точек, для которых все координаты, кроме одной, постоянны (равны 0, либо 1), а четвёртая принимает все возможные значения от 0 до 1.

Прежде всего будем различать четыре группы рёбер: для первой пусть переменной координатой является х (), а y, z, t принимают постоянные значения 0 и 1 во всех комбинациях. Так как существует 8 различных троек из нуля и единицы. Поэтому рёбер первой группы – 8. Рёбер второй группы, для которых переменной является не х, а у, тоже 8. Таким образом, ясно, что всего у четырёхмерного куба 32 ребра. Кроме рёбер у куба есть грани, которые, в свою очередь разделяются на двумерные и трёхмерные грани четырёхмерного куба. У четырёхмерного куба 24 двумерных грани и 8 – трёхмерных (они изображены параллелепипедами (рис. 10)).

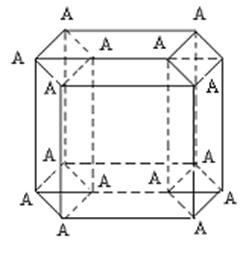
4 - мерный куб Рис. 10

§ 6. Геометрия k-плоскостей в аффинном и евклидовом пространствах

Определение k-плоскости

Пусть в n-мерном аффинном пространстве U_n зафиксирована произвольная точка А, и в соответствующем линейном пространстве L_n зафиксировано произвольное k-мерное подпространство L_k.

Определение. Множество всех точек М аффинного пространства, для которых АМ  L_k, называют k-мерной плоскостью, проходящей через точку А в направлении подпространством L_k.

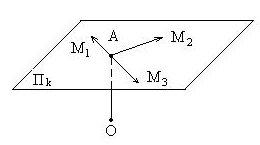
Рис. 11, где k = 2

Говорят также, что L_k есть направляющее подпространство этой плоскости. Очевидно, что каждая плоскость определяет однозначно своё направляющее пространство.

Точку М называют текущей точкой плоскости. На рисунке показаны три положения М₁, М₂, М₃ текущей точки М.

Частные случаи k-плоскостей

Если k = 0, то плоскость состоит из одной точки А. Поэтому каждую точку аффинного пространства можно рассматривать как нуль-мерную плоскость.

Одномерная плоскость называется прямой линией.

Плоскость размерности n – 1 называется гиперплоскостью.

При k = n плоскость совпадает со всем пространством U_n.

В определении плоскости выделена точка А. Докажем, что в действительности все точки плоскости равноправны.

Обозначим плоскость через П_k и зафиксируем произвольную точку В . Надо доказать, что точка М принадлежит плоскости П_k тогда и только тогда, когда  (т. е. что любая точка М может играть роль А).

Пусть . По определению плоскости . Отсюда и по определению подпространства , поэтому . Обратно, если , то  следовательно, .

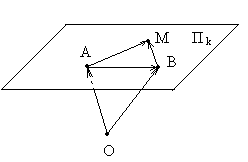
Рис. 12

 

Теорема. Всякая k-мерная плоскость в аффинном пространстве сама является k-мерным аффинным пространством.

Доказательство. Пусть дано аффинное пространство U, которому соответствует линейное пространство L, пусть П_k – плоскость, проходящая через точку А в направлении подпространства L_k. Возьмём в плоскости П_k две произвольные точки M, N . По определению аффинного пространства им соответствует вектор . По определению плоскости векторы АМ и АN принадлежат подпространству L_k.

Следовательно, . Таким образом, каждой упорядоченной паре точек М, N плоскости П_k, поставим в соответствие вектор MN из k-мерного пространства L_k. При этом соблюдаются для П_k аксиомы, вытекающие из определения k-мерной плоскости и для всего аффинного пространства U. Теорема доказана.

Замечание. Если плоскость проходит через начало аффинной системы координат в направлении подпространства L_k, то совокупность радиус-векторов её точек образует подпространство, по определению совпадающее с подпространством L_k.

Пусть в аффинном пространстве U даны точки А₀, А₁,…, А_k (в числе k + 1). Эти точки находятся в общем положении, если они не принадлежат ни одной (k –1)-мерной плоскости .

Проверим, что точки А₀, А₁,…, А_k находятся в общем положении тогда и только тогда, когда векторы А₀А₁,…, А₀А_k линейно независимы (рис. 13), причём безразлично, какую из точек брать в качестве А₀ (то есть за начало векторов, идущих из неё в другие точки).

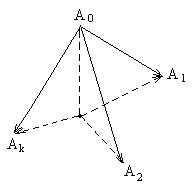
Рис. 13

Из сказанного в этом пункте и из определения плоскости следует, что через систему точек А₀, А₁,…, А_k, находящихся в общем положении, проходит k-мерная плоскость и притом только одна.

Предположим, что в пространстве U_n зафиксирована какая-нибудь аффинная система координат с началом О и базисом е₁, е₂, …, е_n. Рассмотрим плоскость П_k, проходящую через точку А в направлении подпространства L_k.

Будем считать, что точка А имеет координаты р₁, р₂, …, р_n и что L_k задаётся как независимая система векторов q₁, q₂, …, q_k. Тогда радиус-вектор ОМ текущей точки плоскости можно записать в виде

 (6. 1)

где параметры τ₁, τ₂, …, τ_k независимо друг от друга пробегают всевозможные числовые значения, а вектор  (рис. 14)

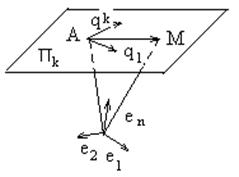Рис. 14

Разложим вектор q₁, q₂, …, q_k по базису е₁, е₂, …, е_n:

 

Координаты текущей точки М обозначим, как обычно, через (x₁, x₂, …, x_n) и запишем векторное равенство в координатах. В результате получим n числовых равенств.

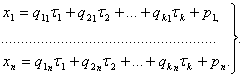 (6. 2)

Эти равенства называются параметрическими уравнениями плоскости П_k.

Пример. Пространство, изучаемое в стереометрии, является трёхмерным аффинным пространством. В нём одномерные и двумерные плоскости совпадают соответственно с прямыми линиями и плоскостями, понимаемыми в элементарно-геометрическом смысле. В отличие от пространства, изучаемого в элементарной геометрии, в аффинном пространстве не определены метрические понятия: расстояния между точками и длины линий, площади и объёмы фигур, углы и перпендикулярность. При исследовании фигур в аффинном пространстве изучаются лишь те геометрические свойства, которые не зависят от метрических понятий.