Уравнение k-сфер

1. Уравнение k-сфер

Определим k-сферы как пересечения сферы с (k+1)-плоскостью. Так как (k+1)-плоскость в свою очередь является пересечением n – k – 1 плоскостей, а каждая из этих плоскостей может быть заменена такой сферой, что указанная плоскость является радикальной плоскостью для этой сферы и данной сферы, k-сфера является пересечением n – k независимых сфер. Поэтому k – сферу можно задать n – k – уравнениями

В этом случае произвольная сфера, проходящая через данную k-сферу, определяется уравнением

  (9. 10)

При k = n – 2 совокупность сфер с уравнениями вида (9. 10) составляет пучок сфер.

Если даны две сферы

, ,

то совокупность сфер с уравнениями

 называется пучком сфер,

содержащем две сферы.

Уравнение при  является уравнением плоскости.

Взаимное расположение двух k-сфер

Две k-сферы k-пространства без общих точек будем называть зацепленными, если всякая сфера, проходящая через одну из этих k-сфер, пересекается со всякой сферой, проходящей через другую k-сферу. Будем называть две k-сферы k-пространства без общих точек незацепленными, если существуют непересекающиеся сферы, проходящие через эти k-сферы.

На рисунке изображены различные виды взаимного расположения двух окружностей в 3-пространстве.

 

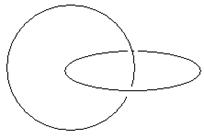
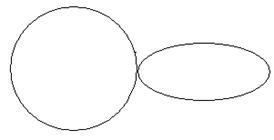
 а) зацепление б) пересечение в точке

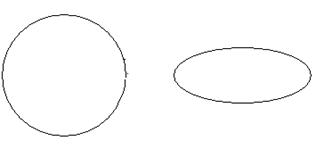
в) незацепление

Рис. 32

Объём сферы

Объём сферы радиуса r, который будем обозначать S_k, выражается интегралом

,

в котором переменное изменяется от 0 до 2p, а переменные  (при i > 1) от  до  поэтому этот интеграл равен произведению k интегралов

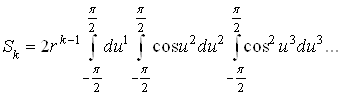
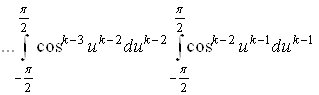
тогда объём S_k сферы радиуса r в k-пространстве при чётном n равен:

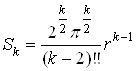  (9. 11)

и для n чётного: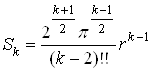

Формулы объёма дают при k = 2 (считая 0!! = 1), 3, 4 и 5 соответственно.

,   .

 

Объём шара

Объём шара радиуса r, который будем обозначать V_k, выражается интегралом

 который с помощью интеграла (9. 11) для вычисления объёма сферы S_k может быть записан в виде

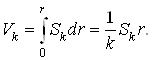
Поэтому объём V_k шара радиуса r в k-пространстве при чётном и нечётном n соответственно равен

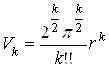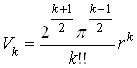 ,  (9. 12)

Формула (9. 12) дает при k = 2, 3, 4, 5 соответственно

 , , ,  (9. 13)

Глава III. Применения многомерной геометрии

§ 10. О необходимости введения многомерного пространства (на примерах задач)

В чём состоит польза многомерных пространств? Где они применяются? Зачем понадобилось расширять представления о пространстве от реального трёхмерного мира до столь далёких абстракций, которые нелегко и не сразу укладываются в сознании?

Для ответа на эти вопросы необходимо рассмотреть несколько примеров задач.

Пример 1. Сумма n чисел равна единице. Каковы должны быть эти числа, чтобы сумма их квадратов была наименьшей?

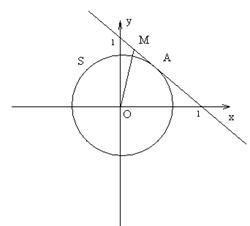
Рис. 33

Решение. Получим ответ на поставленный вопрос геометрическим путём, рассматривая сначала случай n = 2, затем n = 3, а потом обсудим ситуацию при n > 3.

Итак, пусть сначала n = 2. Иначе говоря, рассматривая числа х, у, удовлетворяющие условию х + у = 1, и требуется найти, в каком случае сумма квадратов х² + у² будет наименьшей. Уравнение х + у = 1 определяет на координатной плоскости прямую (рис. 33). Рассмотрим окружность S с центром в начале координат, которая касается этой прямой (точка А). Если точка М(х, у) прямой l отлична от А, то она лежит вне окружности S и поэтому | ОМ| больше радиуса r этой окружности, т. е. . Если же М = А, то сумма х² + у² равна r, т.е. именно для точки А эта сумма принимает наименьшее значение. Точка А имеет координаты х = у = 1/2; это и есть решение поставленной алгебраической задачи при (n = 2).

Рис. 34

Пусть n = 3. Уравнение x + y + z =1 определяет в пространстве плоскость L. Рассмотрим сферу S c центром в начале координат, касающуюся этой плоскости в некоторой точке А (рис. 34). Для любой точки , отличной от А, её расстояние от точки О больше радиуса r сферы S,  и поэтому , при М = А имеем .

Таким образом, именно для точки А сумма  принимает наименьшее значение. Точка А имеет равные координаты: x = y = z (поскольку при повороте пространства, переставляющем оси координат: , и плоскость L и сфера S переходят в себя, а поэтому их общая точка остаётся неподвижной). А так как x + y + z =1, то точка А имеет координаты x = y = z = 1/3; это и есть решение поставленной задачи (для n=3).

Рассмотрим произвольное n; рассуждения будем вести в n-мерном пространстве, точками которого являются последовательности (х₁, х₂, …, х_n), состоящие из n действительных чисел. Уравнение  определяет в этом пространстве «плоскость» L, имеющую размерность n – 1 (гиперплоскость в n-мерном пространстве). Рассмотрим сферу S с центром в начале координат О, касающуюся гиперплоскости L в некоторой точке А. Все точки гиперплоскости L, кроме А, лежат вне сферы S, т. е. находятся от начала координат О на расстоянии, равном r. Следовательно, сумма  принимает наименьшее значение по сравнению со всеми другими точками гиперплоскости L. Заметим теперь, что все координаты точки А равны между собой:  (поскольку поворот пространства, переставляющий оси координат: , и плоскость L и сфера S переходят в себя, а поэтому их общая точка остаётся неподвижной), откуда . Итак, при  сумма квадратов  принимает наименьшее значение для .

Пример 2. На три завода З₁, З₂, З₃ (рис. 35) нужно завести сырьё одинакового вида, которое хранится на двух складах С₁, С₂ в соответствии с данными, указанными в таблице.

Наличие сырья		Потребность в сырье
С1	С2	З1	З2	З3
20 т	25 т	10 т	15 т	20 т

Требуется найти наиболее выгодный вариант перевозок, т. е. вариант, для которого общее количество тонно-километров будет наименьшим.

Решение. Обозначим через х и у количество сырья, которое нужно вывести со склада С₁ соответственно на заводы З₁, З₂. Тогда со второго склада нужно довезти на эти заводы 10 – х и 15 – у тонн сырья. Так как общее количество имеющегося на складах сырья совпадает с потребностью заводов, т. е. всё сырьё должно быть вывезено со складов на заводы, то после обеспечения заводов З₁ и З₂ оставшееся на складах сырьё полностью вывозится на завод З₃, т. е. со склада С₁ на завод З₃ вывозится 20 – х – у, а со склада С₂ 25 – (10 – х) – (15 – у) = х + у тонн.

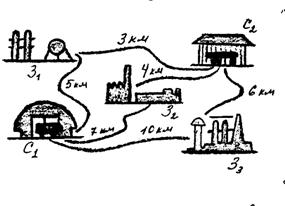
Рис. 35

Учитывая расстояния (рис. 35), находим общее число тонно-километров:

5х + 7у + 10(20 – х – у) + 3(10 – х) – (15 – у) + 6(х + у) = 290 – 2х – у.

Заметим теперь, что все величины, выражающие количество перевозимого по разным дорогам сырья, неотрицательны:

.

Каждое из этих неравенств определяет в системе координат х, у полуплоскость, а система всех неравенств определяет пересечение этих полуплоскостей, т. е. выпуклый многоугольник Q (рис. 36). Заметим, что последнее неравенство можно отбросить: оно является следствием первых двух.

 

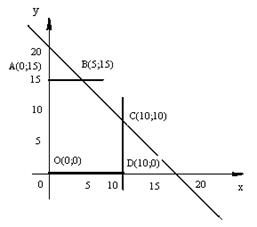
 Рис. 36

Таким образом, задача о нахождении наиболее выгодного варианта перевозок сводится математически к нахождению точки М(х, у) многоугольника Q, в который функция 290 – 2х – у достигает наименьшего значения. Вместо этой функции можно рассматривать функцию – 2х – у.

Действительно, если будет найдено наименьшее значение функции – 2х – у на многоугольнике Q, то прибавив к этому значению 290, получим наименьшее значение функции 290 – 2х – у. На рисунке 37 показано, что наименьшее значение линейной функции, рассматриваемой на многоугольнике Q, достигается в вершине С. Иначе говоря, наиболее выгодный вариант перевозок соответствует точке С(10; 10), т. е. х = 10, у = 10. Общее количество тонно-километров для этих значений х, у равно 290 – 2·10 – 10 = 260. Видно, геометрическая модель позволила полностью решить поставленную задачу.

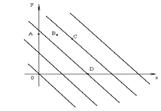 Рис. 37

В рассмотренной задаче все объёмы перевозок со складов на заводы удалось выразить через две переменные х, у. Это позволило дать геометрическую интерпретацию получившейся системы неравенств на координатной плоскости. Допустим, однако, что при тех же двух складах число заводов равно четырём с потребностью в сырье соответственно 8, 10, 12 и 15 т. Тогда нужно будет ввести три переменные x, y, z, обозначающие количество сырья, вывозимого со склада С₁ на первые три завода. Если задать расстояния со складов до заводов, то можно будет составить выражение для общего числа тонно-километров. Можно написать и неравенства, выражающие неотрицательность количества сырья, вывозимого со складов на заводы. Теперь эти неравенства будут зависеть от трёх переменных x, y, z. Каждое из этих неравенств задаёт полупространство, а система всех неравенств определяет пересечение полупространств, т. е. выпуклый многогранник в трёхмерном пространстве.

Таким образом, для четырёх заводов задача о перевозке сырья будет математически формулироваться как задача о наименьшем значении линейной функции на трёхмерном выпуклом многограннике.

Для двух складов и пяти заводов (при сохранении того условия, что всё сырьё должно быть вывезено полностью) потребуются уже четыре переменные, обозначающие количество сырья, вывозимого со склада С₁ на первые четыре завода. Теперь мы будем иметь неравенства с четырьмя переменными, и для получения геометрической интерпретации потребуется четырёхмерное пространство, а при большем числе складов и заводов – пространство ещё большей размерности.

  § 11. Пространство-время классической механики

Аналогия между пространством и временем была известна ещё древним грекам. Аристотель включал время в число непрерывных величин наряду с линиями, поверхностями и телами. Однако впервые рассматривал время как координату наряду с пространственными координатами Галилей.

Время систематически рассматривалось в качестве координаты в теоретической механике.

Будем характеризовать положение материальной точки в пространстве в данный момент времени пространственными координатами хⁱ ( i = 1, 2, 3) и временной координатой t. В классической механике Галилея-Ньютона переход от исходной системы координат хⁱ, t к другой системе, движущейся относительно неё прямолинейно и равномерно определяется формулами

где  - координаты вектора движения первой системы по отношению ко второй. Формулы показывают, что если при переходе от одной системы координат к другой системе, движущейся по отношению к ней, пространственные координаты во второй системе выражаются не только через пространственные координаты в первой системе, но и через временную координату в этой системе, то временные координаты во второй системе могут отличаться от временных координат в первой системе только изменением начала отсчёта, т. е. время в механике Галилея-Ньютона абсолютно.

Механика Галилея-Ньютона хорошо согласуется с практикой при малых скоростях, но при больших скоростях, сравнимых со скоростью света, эта механика заметно расходится с практикой; согласно механике Галилея-Ньютона, если скорость света по отношению к некоторой системе координат равна с, то по отношению к системе координат, движущейся в том же или обратном направлении со скоростью v, эта скорость соответственно должна быть равна c – v или c + v. Но, как показывает эксперимент, скорость света одна и та же по отношению ко всем системам координат, движущихся друг относительно друга прямолинейно и равномерно. Если скорость v, во много раз меньше скорости с, скорости c – v и c + v практически неотличимы от скорости с, но в случае, когда скорость v сравнима со скоростью с, отличие скорости света от скоростей c – v и c + v легко заметить.

  § 12. Пространство-время специальной теории относительности

Для того чтобы выполнялось условие постоянства скорости света для всех систем координат, движущихся равномерно и прямолинейно друг относительно друга, достаточно, чтобы для всех таких систем прямоугольных координат выполнялось соотношение

то есть

  (12. 1)

Это условие не может быть выполнено в механике Галилея-Ньютона, где координата  не может зависеть от координаты . Для того чтобы удовлетворить этому условию, следует отказаться от понятия об абсолютном времени и принять, что пространство и время – не изолированные друг от друга формы существования материи, а две стороны существования одной и той же формы.

Этому условию удовлетворяет механика специальной теории относительности Энштейна, дающая при скоростях, сравнимых со скоростью света, значительно большее согласие с практикой, чем механика Галилея-Ньютона. Если мы обозначим произведение ct, имеющее размерность длины через х⁴, то, согласно специальной теории относительности, при переходе от одной системы координат к другой такой системе, движущейся относительно неё равномерно и прямолинейно, координаты хⁱ (i = 1, 2, 3, 4) преобразуются по закону

  (12. 2)

причём

  (12. 3)

где , .

Формула (12.2) совпадает с формулой преобразования прямоугольных координат обычного n – пространства при n = 4, но формула (12. 3) отличается от соответственного условия в 4-пространстве, в котором .

Поэтому в случае специальной теории относительности можно по аналогии с обычным 4-пространством определить в 4-пространстве, точки которого определяют положения материальных точек в разные моменты времени, расстояния между точками, считая за расстояние между точками М₁ и М₂ с координатами  и  квадратный корень из выражения . Определённое таким образом расстояние может быть как вещественным, так и чисто мнимым и равным нулю. В первом случае существует такая система координат, в которой точки М₁ и М₂ одновременны и расстояние М₁М₂ равно обычному расстоянию между ними в этой системе координат. Во втором случае существует такая система координат, в которой эти точки имеют одинаковые пространственные координаты и расстояние М₁М₂ равно произведению ic на отрезок времени между этими точками в этой системе координат. В третьем случае М₁М₂ = 0 и точки М₁ и М₂ можно соединить лучом света.

Определённое нами 4-пространство называют пространством Минковского. Преобразования (12.2) при , удовлетворяющие условиям (12. 3), называют преобразованиями Лоренца.

Этот пример показывает плодотворность понятия 4-пространства, указывает на необходимость расширения понятия евклидова n-пространства в сторону отказа от знакоопределённости квадратичной формы, выражающей скалярный квадрат вектора х в функции его координат.

  § 13. Пространство-время общей теории относительности

Описание пространства-времени с помощью псевдоевклидова 4-пространства индекса 3 в специальной теории относительности, согласующееся с практикой лучше, чем описание пространства-времени в классической механике, является только приближённым описанием пространства-времени. Следующее приближение было предложено самим Энштейном в его общей теории относительности. Согласно этой теории пространство-время является псевдоримановым 4-пространством индекса 3, кривизна в 2-мерных направлениях которого больше там, где больше плотность материи. Таким образом, не только пространство и время оказываются взаимозависимыми, но их свойства оказываются зависящими от материи, формой существования которой они являются.

Из того, что в малой области геометрия псевдоримановых пространств близка к геометрии псевдоевклидова пространства, образованного векторами в одной из точек этой области, видно, что специальная теория относительности хорошо согласуется с практикой в сравнительно небольших областях пространства-времени, а в больших областях проявляются свойства, описываемые общей теорией относительности.

Хотя с прогрессом науки мы узнаём свойства всё больших областей пространства-времени, известная нам часть вселенной остаётся ограниченной и по свойствам этой части мира мы можем судить о геометрических свойствах мирового пространства-времени в целом только в порядке грубого приближения.

Наиболее грубое приближение к картине мирового пространства-времени в целом мы получим, если предположим, что материя распределена в пространстве–времени совершенно равномерно и, следовательно, пространство-время представляет собой псевдориманово 4-пространство индекса 3 постоянной кривизны. Если мы представим себе такое пространство в виде сферы вещественного или мнимого радиуса в псевдоевклидовом 5-пространстве соответственно индекса 4 или 3, а поверхности t =const также в порядке грубого приближения представим себе сечениями этой сферы параллельными плоскостями, то с течением времени «пространственное сечение» мира уменьшается или расширяется в зависимости от положения секущей плоскости. В первом случае кривизна «пространственного сечения» - постоянная положительная, во втором случае – постоянная отрицательная.

 

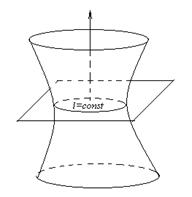
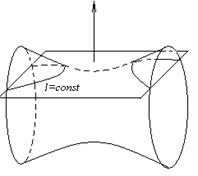
 а) б)

Рис. 38

На рис. 38 изображены трёхмерные аналоги сфер вещественного и мнимого радиуса в псевдоевклидовом 5-пространстве. Изложенная картина мира с первого взгляда кажется неправдоподобной, но она подтверждается астрономическими наблюдениями, свидетельствующими о расширении известной нам вселенной. Это подтверждение указывает на возможность того, что реальное пространство-время, является псевдоримановым пространством переменной кривизны, соответствует этой картине мира «в среднем».

Заключение

Изучение k-мерного пространства весьма полезно как для уяснения многих закономерностей геометрии обычного пространства, являющегося частным случаем k-мерного пространства при k = 3, так и для более наглядного представления многих закономерностей алгебры, геометрии и анализа, связанных с уравнениями с k неизвестными.

Соотношения k-мерной геометрии находят применение и при решении транспортных задач о составлении оптимального способа перевозки грузов и т. д.

В данной работе были рассмотрены многомерные геометрические образы в k-мерных пространствах и четырёхмерное пространство, которое наши глаза никогда не видели. Также исследовались четырёхмерные предметы пространства. На основе изложенного материала исследовали необходимость введения многомерного пространства системы, заданной k-параметрами, в которой появляются понятия k-мерной линии плоскости.

Литература

1.  Александров А. Д., Нецветаева Н. Ю. Геометрия. – М.: Наука, 1990.

2.  Атанасян Л. С. Геометрия. ч. 2 – М., 1987.

3.  Базылев В. Т. и др. Геометрия. Учеб. Пособие для студентов физ.-мат. Факультетов пед. институтов – М.: «Просвещение», 1975.

4.  Вигнер Е. Непостижимая эффективность математики в естественных науках // УФН. – 1968. – Т. 94, вып. 3.

5.  Гельфанд И. М., Глаголева Е. Г., Кириллов Н. А. Метод координат. Изд. 3 – М.: Наука, 1968.

6.  Гордевский Д. З. Популярное введение в многомерную геометрию. – Харьков: Изд-во Харьк. ун-та, 1964.

7.  Ефимов Н. В., Розендорн Э. Р. Линейная алгебра и многомерная геометрия. – М.: Наука, 1970.

8.  Манин Ю. И. Новые размерности в геометрии // Успехи мат. Наук, 1984, т. 39, вып. 6.

9.  Моденов Л. С. Аналитическая геометрия. – М., 1969.

10.  Парнасский И. В. Многомерные пространства. – М.: Наука, 1978.

11.  Понтрягин Л. С. Знакомство с высшей математикой. - Изд. 2. – М.: Наука, 1987.

12.  Прохоров Ю. В. Большой энциклопедический словарь по математике. – М.: Науч. издат., 1998.

13.   Розенфельд Б. А. Многомерные пространства. – М.: Наука, 1966.

14.  Сазанов А. А. Четырёхмерный мир Минковского. – М.: Наука, 1988.

15.   Стрингхем П. Г. Правильные фигуры в n-мерном пространстве. Под ред. Фаге, Успехи математических наук, вып. 10 – М., 1954.

16.   Хлопонина Э. П. Аналитическая геометрия аффинных и евклидовых пространств: Учебное пособие, ч. 1 – Ставрополь: Изд-во СГУ, 1998.