Навигация
2. Объем симплекса.
Прежде всего покажем, что объем ![]() произвольного
произвольного ![]() - симплекса выражается через объем
- симплекса выражается через объем ![]() одной из его
одной из его ![]() - граней и расстояния
- граней и расстояния ![]() от вершины, лежащей против этой грани, до плоскости этой грани по формуле
от вершины, лежащей против этой грани, до плоскости этой грани по формуле
![]() . (8.4)
. (8.4)
 Если будем называть выделенную
Если будем называть выделенную ![]() -грань
-грань ![]() - симплекса его основанием, а расстояние
- симплекса его основанием, а расстояние ![]() - его высотой, то формула (8.4) показывает, что объем
- его высотой, то формула (8.4) показывает, что объем ![]() - симплекса равен
- симплекса равен ![]() произведение его основания на высоту. Пусть основание k – симплекса
произведение его основания на высоту. Пусть основание k – симплекса ![]() (на рисунке 28 изображается
(на рисунке 28 изображается ![]() при
при ![]() )
)
Проведем плоскость, параллельную плоскости ![]() - грани
- грани ![]() на расстоянии
на расстоянии ![]() от нее. Это плоскость высечет из нашего k – симплекса
от нее. Это плоскость высечет из нашего k – симплекса ![]() -симплекс
-симплекс ![]() и отсечет от него k – симплекс
и отсечет от него k – симплекс ![]() , Обозначим
, Обозначим ![]() -симплекса
-симплекса ![]() через
через ![]() , то формулу для определения объема k – симплекса можно записать в виде
, то формулу для определения объема k – симплекса можно записать в виде
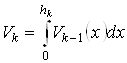 . (8.5)
. (8.5)
Так как k – симплекса ![]() может быть получен из k – симплекса
может быть получен из k – симплекса ![]() гомотетией с центром в вершине
гомотетией с центром в вершине ![]() и с коэффициентом
и с коэффициентом 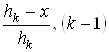
![]() получается из
получается из ![]() - грани
- грани ![]() той же гомотетией. Так как матрица гомотетии, отображающей
той же гомотетией. Так как матрица гомотетии, отображающей ![]() - грань
- грань ![]() на
на ![]() - грань
- грань ![]() является матрицей
является матрицей ![]() -20 порядка вида
-20 порядка вида 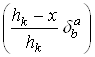 , определить этой матрицы равен
, определить этой матрицы равен  и объем
и объем ![]() может быть записан в виде
может быть записан в виде
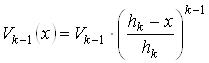 .
.
Поэтому
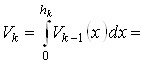
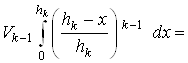
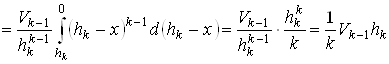 .
.
Применяя формулу (4) к объему ![]()
![]() - грани, выразим этот объем через объем
- грани, выразим этот объем через объем ![]() одной из ее
одной из ее ![]() - граней и соответственную высоту
- граней и соответственную высоту ![]() этой
этой ![]() - грани. Аналогично выразим объемы
- грани. Аналогично выразим объемы ![]() ,
, ![]() , … ,
, … , ![]() и площадь
и площадь ![]() , вложенных друг в друга
, вложенных друг в друга ![]() - грани,
- грани, ![]() - грани, …, 3-грани и 2-грани симплекса через объемы
- грани, …, 3-грани и 2-грани симплекса через объемы ![]() , …,
, …, ![]() , площадь
, площадь ![]() и длину
и длину ![]() одного из ребер
одного из ребер ![]() - симплекса и соответственные высоты
- симплекса и соответственные высоты ![]() ,
, ![]() , … ,
, … , ![]() этих граней, получим что
этих граней, получим что
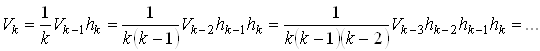
![]() .
.
В том случае, когда k – симплекс определяется уравнением (1), где ![]() , произведение
, произведение ![]()
![]()
![]() …
…![]()
![]() равно объему k – параллелепипеда, определяемого уравнением
равно объему k – параллелепипеда, определяемого уравнением
![]() с векторами
с векторами ![]() при 0
при 0![]() , поэтому объем
, поэтому объем ![]() k – симплекса связан с объемом
k – симплекса связан с объемом ![]() соответствующего k – параллелепипеда соотношением
соответствующего k – параллелепипеда соотношением
![]() =
=![]()
![]() . (8.6)
. (8.6)
Так как квадрат объема ![]() в силу (7.6 из § 7) равен определителю Грамма, составленному из вектора
в силу (7.6 из § 7) равен определителю Грамма, составленному из вектора ![]() , из формулы (8.6) вытекает, что объем
, из формулы (8.6) вытекает, что объем ![]() k – симплекса, определяемого уравнением (8.1), где
k – симплекса, определяемого уравнением (8.1), где ![]()
![]() , определяется соотношением
, определяется соотношением
 (8.7)
(8.7)
Объем ![]()
![]() – симплексa, определяемого уравнением (8.1) при
– симплексa, определяемого уравнением (8.1) при ![]() =
= ![]() , где
, где ![]() , равен
, равен
![]() =
=![]()
![]() , (8.8)
, (8.8)
квадрат косого произведения (![]() ) равен определителю Грамма, составленному из векторов
) равен определителю Грамма, составленному из векторов ![]() .
.
Похожие работы
... работы австрийского геометра Эрвина Круппа, получившие развитие в трудах русских ученых Н.А. Глаголева, Н.Ф. Четверухина. В середине XIX века зарождается и получает развитие начертательная геометрия многих измерений - многомерная геометрия. Итальянский математик Веронезе и голландский ученый Скаутте дают начало этому новому направлению. В России многомерная начертательная геометрия развивалась в ...
... рода: перейти к новому образу рациональности. На смену диалектике "единства противоположностей" (как в гегелевской, так и в марксистской ее интерпретации) приходит интервальная диалектика постижения многомерного мира. "Синтез противоположностей" заменяется конструированием соответствующих конфигураций интервалов. В истории познавательного освоения мира человеком можно встретить различные случаи ...
... временные и пространственные отличие установлены, таково и само нечто. Подобного же необходимого порядка мы ждем и от категориальной системы, классифицирующей сложные предметы материальной культуры. 2. Концепция многомерной онтологии. Прежде чем вернуться к техническим предметам материальной культуры, мы рассмотрим традиционную онтологию. Мы ждем, что эта традиция укажет ориентиры и нашему ...
... нельзя дать единое определение основных понятий для всех геометрий, то основные понятия геометрии следует определить как объекты любой природы, удовлетворяющие аксиомам этой геометрии. Таким образом, при аксиоматическом построении геометрической системы мы исходим из некоторой системы аксиом, или аксиоматики. В этих аксиомах описываются свойства основных понятий геометрической системы, и мы можем ...
0 комментариев