Уравнения k-плоскости по k+1 точкам

2. Уравнения k-плоскости по k+1 точкам

Если заданы k+1 точек А₀(х₀), А₁(х₁), …, А_n(х_n) и векторы А₀А_{а =} х_а – х₀ независимы, то эти точки определяют единственную k – плоскость, проходящую через них: в этом случае за направляющие векторы этой плоскости можно принять векторы А₀А_а и векторное уравнение k-плоскости можно записать в виде

 (6. 3)

Будем называть k-плоскость, определяемую точками А₀(х₀), А₁(х₁), …, А_n(х_n), k-плоскостью А₀, А₁, …, А_k.

Случай k = n-1

В дальнейшем будем часто иметь дело с k-поверхностями и k-плоскостями при k = n – 1. Говоря, «поверхность n-пространства» и «плоскость n-пространства», но иметь в виду (n – 1)-поверхность и (n – 1)-плоскость этого пространства. Часто поверхность и плоскость называется соответственно гиперповерхностью и гиперплоскостью.

Поверхность можно задать одним координатным уравнением

 (6. 4)

если координаты xⁱ, удовлетворяющие этому уравнению, можно представить как функции n – 1 параметров t₁, t₂, …, t_n-1, то получим

F(x) = 0. (6. 5)

3. Взаимное расположение плоскостей

3. 1 Пересекающиеся плоскости

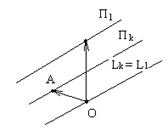
Во всём этом пункте размерности плоскостей и подпространств обозначены индексами снизу. Пусть две плоскости П_k и П_l пересекаются, то их пересечением является некоторая плоскость П_m.

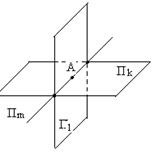 k = l = 2, m = 1 Рис. 15

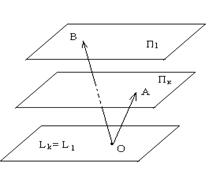
Замечание 1. Не исключена возможность, что П_m состоит из одной точки (m = 0). Это видно на примере двух пересекающихся прямых или прямой и плоскости (рис. 16).

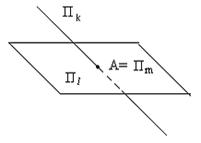
Рис. 16

В общем случае по одной точке могут пересекаться две плоскости, сумма разностей которых не превышает размерности пространства, например, двумерные плоскости в четырёхмерном пространстве.

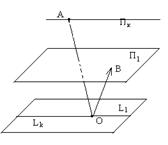
Замечание 2. Не исключено и другое, когда одна из двух плоскостей целиком принадлежит другой. Например, , тогда  (рис. 17)

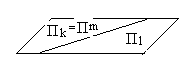k = m = 1, l = 2

Рис. 17

2) Если плоскости П_k и П_l пересекаются по плоскости П_m, то существует единственная плоскость П_r, размерности r = k + l – m, содержащая П_k и П_l, причём ни в какой плоскости меньшей размерности П_k и П_l не могут одновременно поместиться. Направляющее подпространство L_r плоскости П_r является суммой направляющих подпространств L_k и L_l. Эта сумма является прямой суммой тогда и только тогда, когда П_k иП_l пересекаются по одной точке (m = 0, см. рис. 18).

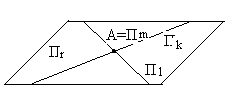
Рис. 18

В частном случае, когда n = k + l – m, роль плоскости П_r выполняет всё пространство U_n (при r = n = 3 см. рис. 15).

3) Если пересекающиеся плоскости П_k и П_l содержатся в какой-нибудь плоскости П_r, то размерность их пересечения . В частности,  для любых двух непересекающихся плоскостей из U_n.

4) Если плоскости П_k и П_l проходят через точку А в направлении подпространств L_k и L_l соответственно и если L_k содержится в L_l, то плоскость П_k содержится в плоскости П_l. Если при этом k = l, то П_k совпадает с П_l (также и L_k совпадает с L_l).

Параллельные плоскости

Пусть теперь плоскость П_k определяется точкой А и подпространством L_k, а плоскость П_l – точкой В и подпространством L_l. Будем считать, что .

Определение: Плоскость П_k параллельна плоскости П_l, если .

В этом случае плоскость П_l параллельна плоскости П_k.

Замечание 1. Согласно этому определению включение  является частным случаем параллельности.

Замечание 2. Если П_k параллельна П_l, причём k = l, то L_k совпадает с L_l.

Замечание 3. Убедимся, что при n = 3 частные случаи k = l = 1,

k = l = 2 и k =1, l = 2 согласуются с понятием параллельности прямых и плоскостей, известным из элементарной геометрии (рис. 19)

 а) б) в)

Рис. 19

Пусть в произвольной аффинной системе координат две плоскости П и П^l одинаковой размерности заданы системами линейных уравнений. Пользуясь определением параллельности, нетрудно установить следующее утверждение.

Утверждение. Для того, чтобы П и П^’ были параллельными, необходимо и достаточно, чтобы соответствующие однородные системы уравнений были эквивалентны.

В частности, две гиперплоскости параллельны тогда и только тогда, когда в одних и тех же координатах они задаются уравнениями

 и (6. 6)

 (6. 7)

с пропорциональными коэффициентами при переменных:

.

Теорема 1. Пусть в аффинном пространстве U_n даны плоскость П_k и точка В. Тогда существует единственная плоскость  размерности k, проходящая через точку В параллельно П_k. Если , то  совпадает с П_k; если точка В расположена вне П_k, то плоскости П_k и  не пересекаются.

Скрещивающиеся плоскости

Определение. Две плоскости называются скрещивающимися, если они не пересекаются и не параллельны.

Известно, что в трёхмерном пространстве U₃ две прямые линии, т. е. одномерные плоскости, могут скрещиваться, тогда как прямая линия и двумерная плоскость в U₃ скрещиваться не могут. С повышением размерности пространства оно становится более просторным, в результате чего появляется возможность строить в нём скрещивающиеся плоскости разных размерностей, а не только одномерные. Ниже сформулирована теорема 2, содержание которой можно рассматривать как общий приём построения скрещивающихся плоскостей. Именно, пусть в аффинном пространстве U_n дана плоскость П_l (l < n). Возьмём произвольную плоскость П_k так, чтобы П_k и П_l не были параллельны и пересекались; плоскость, по которой они пересекаются, обозначим через П_m. Пусть П_r - плоскость наименьшей размерности, содержащая П_k и П_l. Мы знаем, что r = k + l – m.

Теорема 2. Если , то всякая k-мерная плоскость, которая параллельна П_k и не лежит в П_r, скрещивается с П_l.

Следствие. Если целые числа k, l, m, n удовлетворяют неравенствам

, , , то в U_n найдутся скрещивающиеся плоскости П_k и П_l с направляющими подпространствами L_k и L_l, пересечение которых  имеет размерность m.

Доказательство теоремы 2. Так как , то плоскость П_r не исчерпывает собой всего пространства U_n. Это позволяет взять (с большим произволом) точку С, не лежащую в П_r. Обозначим через  плоскость размерности k, проходящую через точку С, параллельно П_k. Ясно, что  не содержится в П_r и что, выбирая по-разному точку С, мы можем получить любую k-мерную плоскость, удовлетворяющую условию теоремы. (См. рис. 14, на котором k = l = 2, r = 2, n = 4, и трёхмерные плоскости условно изображены в виде параллелепипеда).

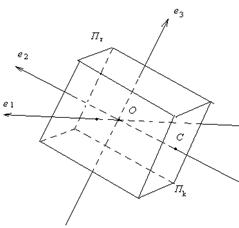
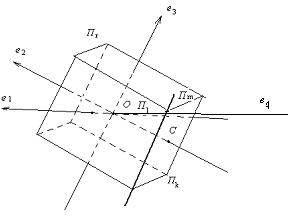
Рис. 20

Докажем, что плоскости П_l и  скрещиваются. Заметим, что плоскость  не параллельна П_l, так как в противном случае или , или , что противоречит условию расположения плоскостей П_k и П_l.

Теперь докажем, что  и П_l не пересекаются. Проведём через точку С вспомогательную r-мерную плоскость , параллельную П_r. Тогда  и поэтому П_k не может пересечь П_l ибо в противном случае точка их пересечения  принадлежала бы параллельным плоскостям П_r и . Следовательно, скрещивается с П_l. Теорема 2 доказана.

Пусть в n-мерном аффинном пространстве U_n даны скрещивающиеся плоскости П_k и П_l с направляющими подпространствами L_k и L_l, причём

, .

Теорема 3. Существует единственная плоскость П_r+1 размерности , содержащая плоскости П_k и П_l.

Доказательство. Возьмём произвольную точку  и зафиксируем произвольную точку ; обозначим через  линейную оболочку вектора  (рис. 16). Допустим, что существует какая-то плоскость , содержащая П_k и П_l; пусть  - её направляющее подпространство. Очевидно, что  должно содержать L_k, L_l и , а следовательно, и сумму этих подпространств. Обозначим эту сумму через L_r+1:

Обратно, если  - любое подпространство, включающее L_r+1, то , проходящая через точку А в направлении , будет содержать П_k и П_l. В самом деле, так как  и, то; так как , то , так как  и , то .

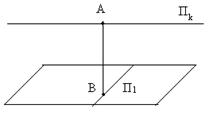
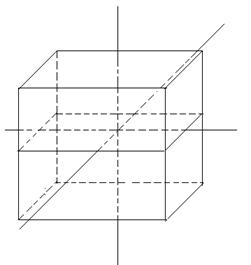
Рис. 21

Получим среди всех плоскостей  искомую плоскость П_r+1 минимальной размерности r + 1 в том единственном случае, когда в качестве  берётся L_r+1. Подсчитаем r + 1. С этой целью рассмотрим  и обозначим размерность  через р. По теореме 3 (в n-мерном пространстве L имеются подпространства L_k и L_l, размерности которых соответственно равны k и l. Если их пересечение имеет размерность m, то размерность их суммы L_k + L_l равна r = k + l – m) имеем р = k + l – m.

Покажем, что  есть прямая сумма, поэтому размерность L_r+1 равна р + 1, то есть (r + 1) = (k + l – m) +1.

Для этого достаточно показать, что вектор  не принадлежит пространству . Предположим противное. Пусть . Тогда по определению суммы подпространств существуют векторы х и у такие, что, , . (v) По первой аксиоме аффинного пространства найдётся точка С такая, что , причём . По второй аксиоме аффинного пространства . (vv)

Учитывая (v), (vv), находим, что , так что . Получается, что плоскости П_k и П_l имеют общую точку С, но это невозможно, поскольку плоскости П_k и П_l скрещиваются. Теорема 3 доказана.

Замечание. Рисунок 20 лишь частично иллюстрирует теорему 3. Например, если размерности П_k и П_l больше m и различны между собой, , то, как,

Проведённые выше рассуждения показывают, что плоскости П_k и П_l, о которых идёт речь в теореме 3, не содержатся ни в какой плоскости меньшей размерности, чем r + 1.

Сохраняя обозначения предыдущего подпункта, сформулируем достаточное условие пересечения двух плоскостей.

Теорема 4. Если в U_n даны плоскости П_k и П_l, такие, что , где m – размерность пересечения L_m направляющих подпространств L_k и L_l, то П_k и П_l пересекаются.

Доказательство. Исключая тривиальный случай, когда какая-нибудь из данных плоскостей совпадает со всем пространством, имеет

В расположении двух данных плоскостей могут быть лишь три возможности:

либо П_k параллельна П_l;

либо плоскости П_k и П_l скрещиваются;

либо они пересекаются.

Если П_k параллельна П_l, то для размерности m пересечения соответствующих им пространств L_k и L_l имеем m = min (k, l). Теорема доказана.