Навигация
Аффинность k – симплексов
3. Аффинность k – симплексов.
Если даны два произвольных k – симплекса ![]() и
и ![]() , то системы их вершин определяют аффинное преобразование, переводящее первую из этих систем вершин во вторую.
, то системы их вершин определяют аффинное преобразование, переводящее первую из этих систем вершин во вторую.
Так как при аффинном преобразовании плоскости переходят в плоскости, это аффинное преобразование переводит весь k – симплекс ![]() в k – симплекс
в k – симплекс ![]() . Поэтому всякие два k – симплекса аффинны.
. Поэтому всякие два k – симплекса аффинны.
Относительный объем k – симплекса, определяемого уравнением (8.1) при ![]() =
= ![]() , где
, где ![]() , выражается по формуле при аффинном преобразовании с оператором
, выражается по формуле при аффинном преобразовании с оператором ![]() умножается на определитель матрицы оператора
умножается на определитель матрицы оператора ![]() , получаем, что при аффинном преобразовании относительные объемы всех k – симплексов умножаются на определитель матрицы этого аффинного преобразования, т.е. если k – симплекс с относительным объемом
, получаем, что при аффинном преобразовании относительные объемы всех k – симплексов умножаются на определитель матрицы этого аффинного преобразования, т.е. если k – симплекс с относительным объемом ![]() переходит при аффинном преобразовании с матрицей
переходит при аффинном преобразовании с матрицей ![]() в k – симплекс с объемом
в k – симплекс с объемом ![]() , то, так же как в случае k – параллелепипедов,
, то, так же как в случае k – параллелепипедов,
![]() =
=![]()
![]()
![]() . (8.9)
. (8.9)
Отсюда вытекает, что отношения объемов k – симплексов не изменяются при аффинных преобразованиях.
Правильный k – симплекс
Определение правильных многоугольников и многогранников позволяет определить правильный k – симплекс.
Прежде всего построим правильный k – симплекс. Правильный k – симплекс при ![]() = 2 – равносторонний треугольник. Равносторонний треугольник
= 2 – равносторонний треугольник. Равносторонний треугольник ![]() с центром в начале координат и со стороной
с центром в начале координат и со стороной ![]() на прямой
на прямой ![]() имеет вершины в точках с координатами
имеет вершины в точках с координатами ![]() ,
, ![]() и
и ![]() .
.
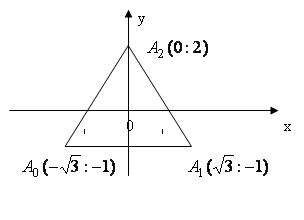
Рис. 29
Для построения правильного k – симплекса ![]() с центром в начале системы прямоугольных координат и с гранью
с центром в начале системы прямоугольных координат и с гранью ![]() на плоскости
на плоскости ![]() предположим, что мы построили аналитичный правильный
предположим, что мы построили аналитичный правильный ![]() - симплекс.
- симплекс.
Так как центр О k – симплекса делит отрезок прямой ![]() между точкой
между точкой ![]() и плоскостью
и плоскостью ![]() в отношении
в отношении ![]() : 1, а прямая
: 1, а прямая ![]() совпадает с
совпадает с ![]() -ой координатной осью, вершина
-ой координатной осью, вершина ![]() имеет координаты (0, 0, 0, …
имеет координаты (0, 0, 0, …![]() );
); ![]() -е координаты вершин
-е координаты вершин ![]() равны – 1, а первые
равны – 1, а первые ![]() -1 координаты этих вершин можно получить из координат вершин (
-1 координаты этих вершин можно получить из координат вершин (![]() -1) - симплекса
-1) - симплекса ![]() умножением их на такой множитель
умножением их на такой множитель ![]() , чтобы все расстояния
, чтобы все расстояния ![]() ,
, ![]() , …,
, …, ![]() =
=![]() =
=![]()
Расстояние от центра построенного ![]() - симплекса
- симплекса ![]() до его (
до его (![]() -1) – граней равно 1, а расстояние от того же центра до вершин этого
-1) – граней равно 1, а расстояние от того же центра до вершин этого ![]() - симплекса равно
- симплекса равно ![]() . Длина каждого из ребер этого
. Длина каждого из ребер этого ![]() - симплекса равна
- симплекса равна ![]() .
.
 Из определения правильного
Из определения правильного ![]() - симплекса видно, что все
- симплекса видно, что все ![]() - грани правильного
- грани правильного ![]() - симплекса являются правильными
- симплекса являются правильными ![]() - симплексами.
- симплексами.
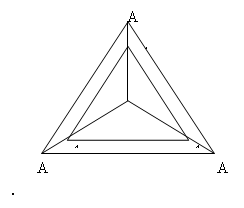
Рис.30
На рисунке изображен правильный (![]() -1) – симплекс (
-1) – симплекс (![]() = 4)
= 4)
Объем правильного ![]() - симплекса.
- симплекса.
Вычислим объем построенного правильного симплекса. Так как объем основания этого ![]() - симплекса равен произведению
- симплекса равен произведению ![]() , а высота этого
, а высота этого ![]() - симплекса равна
- симплекса равна ![]() +1, получаем, что
+1, получаем, что

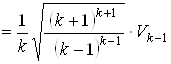 .
.
 .
.
При ![]() = 2 формула дает нам
= 2 формула дает нам ![]() .
.
При ![]() = 3 формула
= 3 формула ![]() .
.
Объем правильного ![]() - симплекса, (
- симплекса, (![]() -1) – грани которого находятся на расстоянии
-1) – грани которого находятся на расстоянии ![]() от его центра, равен
от его центра, равен
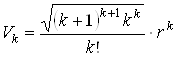 .
.
Называть k-мерной сферой евклидова k-пространства или k-сферой этого пространства множество всех точек этого пространства, лежащих в одной (k + 1)-плоскости и отстоящих от данной точки, называемой центром k-сферы, на одном и том же расстоянии, называемом радиусом k-сферы.
При k = n – 1 k-сфера определяется как множество всех точек пространства, отстоящих от одной точки на одном и том же расстоянии: в дальнейшем, говоря «сфера», будем иметь в виду (n – 1)-сферу. При k = 1, k-сфера называется окружностью.
Если радиус (k– 1)-сферы равен R, то множество всех точек k-плоскости этой (k– 1)-cферы, находящихся от центра (k– 1)-cферы на расстоянии ![]() , называется k-шаром. При k = n n-шар определяется как множество всех точек n-пространства, отстоящих от центра сферы на расстоянии
, называется k-шаром. При k = n n-шар определяется как множество всех точек n-пространства, отстоящих от центра сферы на расстоянии ![]() . В дальнейшем, говоря «шар», будем иметь в виду n-шар. При k = 2 k-шар называется кругом.
. В дальнейшем, говоря «шар», будем иметь в виду n-шар. При k = 2 k-шар называется кругом.
Если центр сферы – точка М0(х0), а радиус равен R (рис. 31), радиус-вектор х произвольной точки М сферы связан условием, состоящим в том, что расстояние М0М равно R. Так как это расстояние равно модулю вектора ![]() , т. е.
, т. е. ![]() , то уравнение сферы с центром в точке М0, и радиусом R имеет
, то уравнение сферы с центром в точке М0, и радиусом R имеет
![]() (9. 1)
(9. 1)
или, после возведения обеих частей уравнения (9. 1) в квадрат
![]() (9. 2)
(9. 2)
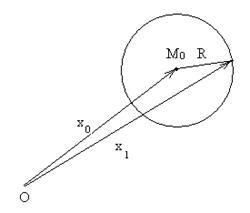
Рис. 31
Уравнению (9. 2) не удовлетворяет радиус-вектор ни одной точки, для которой расстояние М0М не равно R, так как и расстояние М0М и радиус R – положительные числа.
Уравнение (9. 2) называется векторным уравнением сферы. Это уравнением сферы. Это уравнение является частным случаем векторного уравнения поверхности. Поэтому сфера является частным случаем уравнения поверхности, так как k-сферу можно рассматривать как сферу в (k + 1)-пространстве.
Так как k-сфера с центром в точке М0(х0) и радиусом в некоторой (k + 1)-плоскости является пересечением сферы с тем же центром и радиусом с указанной (k + 1)-плоскостью, уравнениями k-сферы является уравнение (9. 2) сферы с тем же центром и радиусом и уравнения (k + 1)-плоскости.
Если центр сферы находится в начале, х0=0, то уравнение (9. 2) примет вид
![]() (9. 3)
(9. 3)
Уравнение (9. 2) можно переписать в виде
![]() (9. 4)
(9. 4)
или, умножая обе части этого равенства на число а, в виде
![]() (9. 5)
(9. 5)
Вектор ![]() и число с в уравнении (9. 5) связаны с радис-вектором х0 центра сферы и её радиусом R соотношениями
и число с в уравнении (9. 5) связаны с радис-вектором х0 центра сферы и её радиусом R соотношениями
![]() ,
, ![]() (9. 6)
(9. 6)
Поэтому, если дано уравнение (9. 5) сферы, то центр и радиус этой сферы определяются соотношениями.
![]() ,
, 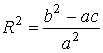 (9. 7)
(9. 7)
Уравнение (9. 5) при а = 1, т. е. уравнение
![]() (9. 8)
(9. 8)
называется нормальным уравнением сферы. В случае нормального уравнения сферы соотношения (9. 7) показывает, что, для того чтобы уравнение (9. 5) было уравнением сферы, необходимо выполнение неравенства
![]() (9. 9)
(9. 9)
В случае, когда ![]() , уравнению (9. 5) удовлетворяет только одна точка М0(х0), которую можно рассматривать как сферу нулевого радиуса. Для того, чтобы общее уравнение второй степени было бы уравнением сферы, необходимо выполнение неравенства, равносильного неравенству (9. 9).
, уравнению (9. 5) удовлетворяет только одна точка М0(х0), которую можно рассматривать как сферу нулевого радиуса. Для того, чтобы общее уравнение второй степени было бы уравнением сферы, необходимо выполнение неравенства, равносильного неравенству (9. 9).
Геометрия k-сфер
Похожие работы
... работы австрийского геометра Эрвина Круппа, получившие развитие в трудах русских ученых Н.А. Глаголева, Н.Ф. Четверухина. В середине XIX века зарождается и получает развитие начертательная геометрия многих измерений - многомерная геометрия. Итальянский математик Веронезе и голландский ученый Скаутте дают начало этому новому направлению. В России многомерная начертательная геометрия развивалась в ...
... рода: перейти к новому образу рациональности. На смену диалектике "единства противоположностей" (как в гегелевской, так и в марксистской ее интерпретации) приходит интервальная диалектика постижения многомерного мира. "Синтез противоположностей" заменяется конструированием соответствующих конфигураций интервалов. В истории познавательного освоения мира человеком можно встретить различные случаи ...
... временные и пространственные отличие установлены, таково и само нечто. Подобного же необходимого порядка мы ждем и от категориальной системы, классифицирующей сложные предметы материальной культуры. 2. Концепция многомерной онтологии. Прежде чем вернуться к техническим предметам материальной культуры, мы рассмотрим традиционную онтологию. Мы ждем, что эта традиция укажет ориентиры и нашему ...
... нельзя дать единое определение основных понятий для всех геометрий, то основные понятия геометрии следует определить как объекты любой природы, удовлетворяющие аксиомам этой геометрии. Таким образом, при аксиоматическом построении геометрической системы мы исходим из некоторой системы аксиом, или аксиоматики. В этих аксиомах описываются свойства основных понятий геометрической системы, и мы можем ...
0 комментариев