Навигация
Геометрическая интерпретация динамической системы на фазовой плоскости (х, у)
4. Геометрическая интерпретация динамической системы на фазовой плоскости (х, у)
Геометрическая интерпретация системы (I) в трехмерном пространстве (х, у, t) в настоящей книге является вспомогательной. Основная геометрическая интерпретация автономной системы (1)связана с рассмотрением плоскости (х, у). Эта плоскость называется фазовой плоскостью системы (I).
Будем в каждой точке М (х, у) области G плоскости (х, у) рассматривать вектор v с компонентами Р (х, у), Q (x, у). Динамическая система (I) определяет, таким образом, в области G векторное поле *).
В силу того, что Р (х, у) и Q (х, у) по предположению имеют непрерывные частные производные, векторное поле, определяемое системой (I), является так называемым непрерывно дифференцируемым векторным полем.
Пусть в точке М (х, у) хотя бы одна из величин Р (х, у), Q (х, у) не обращается в нуль. Тогда длина вектора в этой точке
![]()
отлична от нуля, а синус и косинус угла ![]() (x, у) между положительным направлением оси х и направлением вектора даются выражениями
(x, у) между положительным направлением оси х и направлением вектора даются выражениями
![]()
В тех точках, в которых одновременно Р (х, у), Q (x, у).
длина вектора обращается в нуль, а направление вектора становится неопределенным. Такие точки называются особыми точками векторного поля (или особыми точками системы (1)); точки, в которых хотя бы одна из величин Р (x, у), Q (х, у) не равна нулю,— обыкновенными или неособыми точками этого векторного поля. Во всякой неособой точке М векторного поля угол ![]() (x, у), непрерывен. В особой точке угол
(x, у), непрерывен. В особой точке угол ![]() (x, у) неопределен, и при стремлении
(x, у) неопределен, и при стремлении ![]() и
и ![]() к координатам особой точки lim
к координатам особой точки lim![]() может не существовать.
может не существовать.
Пусть
![]() (11)
(11)
— какое-нибудь решение системы (I). Множество точек М (![]() (t), ψ (t)), где t принимает все значения, при которых определено решение (11), называется траекторией, соответствующей данному решению, а также траекторией векторного поля, заданного динамической системой (І), или просто траекторией данной динамической системы (а также иногда фазовой траекторией).
(t), ψ (t)), где t принимает все значения, при которых определено решение (11), называется траекторией, соответствующей данному решению, а также траекторией векторного поля, заданного динамической системой (І), или просто траекторией данной динамической системы (а также иногда фазовой траекторией).
Уравнения (11), очевидно, являются параметрическими уравнениями траектории. Обратно, если дана какая-нибудь траектория, то решение, которому она соответствует, мы будем называть решением, соответствующим данной траектории.
В математической литературе весьма употребительно векторное обозначение для системы дифференциальных уравнений. Система (I) в этом обозначении запишется в виде векторного уравнения
![]() = F(x)
= F(x)
Векторное обозначение чрезвычайно удобно при рассмотрении систем, состоящих из большого числа уравнении. Однако в рассмотренном нами случае системы только двух дифференциальных уравнении в этом обозначении нет особой необходимости, п мы не будем пользоваться им для того, чтобы не загромождать изложение различными символиками.]
Если точка М (х, у) траектории не является особой точкой векторного поля, то вектор (Р (х, у), Q (х, у)) является касательным вектором к траектории (рис. 2). Действительно, в силу того, что
![]()
есть решение системы (I), имеют место тождества
![]() (12)
(12)
Но вектор с компонентами ![]() (t),
(t), ![]() (t), очевидно, является касательным вектором к траектории, и в силу равенств (12) он совпадает с вектором поля, заданного системой (I).
(t), очевидно, является касательным вектором к траектории, и в силу равенств (12) он совпадает с вектором поля, заданного системой (I).
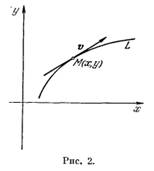
Рассматривая параметр t как «время», можно дать следующую «кинематическую» интерпретацию системы (I): решение
![]()
можно рассматривать как закон движения точки по траектории на фазовой плоскости. В каждой точке фазовой плоскости вектор, заданный системой (I), т. е. вектор Р(х, у), Q (х, у), очевидно, равен скорости движущейся точки или «фазовой скорости». Решениям с одними и теми же начальными значениями х0 и у0 и различными начальными значениями t0 соответствуют движения, начинающиеся в одной и той же точке, но в различные начальные моменты «времени» (t0 и t*). Точка с координатами (![]() ) называется также «изображающей» или «представляющей» точкой.
) называется также «изображающей» или «представляющей» точкой.
Пусть М (a,b) — особая точка системы (I), так что
P(a,b)=Q(a,b) (13)
Тогда, очевидно, х = a, у = b есть решение системы (I), и, следовательно, особая точка векторного поля сама является отдельной траекторией. Такая траектория называется состоянием равновесия *). Очевидно, также обратно, если у системы (I) есть решение
х = а, y= b (14)
(а и b — некоторые постоянные), то точка a, b непременно является состоянием равновесия (особой точкой векторного поля), т. е. для нее выполняются равенства (13). Решение (14), очевидно, вследствие того, что t в него не входит, определено для всех t.
В дальнейшем для точек х, у области G, для которых Р (х, у) =0, Q (х, у) = 0, в основном будет использоваться термин «состояние равновесия» (а не особая точка).
Состояние равновесия М (а, Ь) системы (I) называется изолированным, если существует ![]() > 0 такое, что в
> 0 такое, что в ![]() -окрестности кроме М не лежит уже более ни одного состояния равновесия.
-окрестности кроме М не лежит уже более ни одного состояния равновесия.
Похожие работы
... для реализации системы бюджетирования Консультационной группы "Воронов и Максимов". Статья о проблемах выбора системы бюджетирования - в проекте "УПРАВЛЕНИЕ 3000". Бюджетный автомат Если вы решитесь на автоматизацию системы бюджетирования компании, перед вами сразу встанут вопросы: что выбрать, сколько платить, как внедрять. Примеряйте! О ЧЕМ РЕЧЬ В “Капитале” на стр. 44, 45 мы рассказали ...
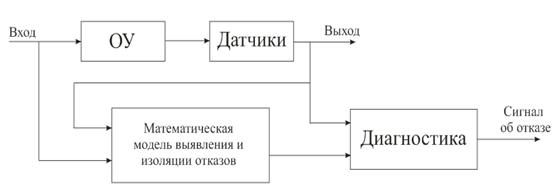
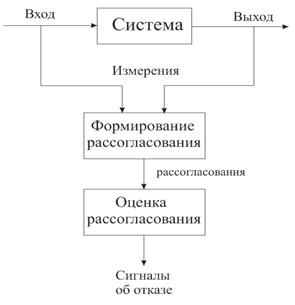
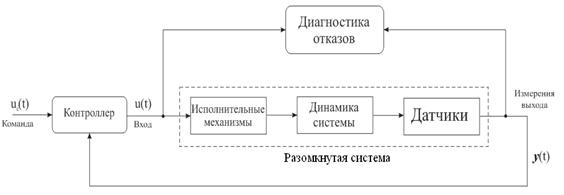
... сети могут быть использованы как классификаторы для разделения образцов рассогласований и формирования сигналов тревог. Таким образом, они могут выявлять и изолировать отказы. 3. Диагностика отказов системы регулирования уровня жидкости в баке 3.1. Постановка задачи Реализацию описанного выше метода диагностики отказов, основанного на моделях будем выполнять применительно к системе ...
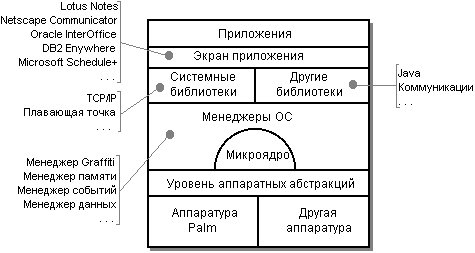
... их интеграция, расширение их возможностей в новых версиях, создание новых средств и перенос их на другие аппаратные платформы и в другие ОС IBM. 12.4 Операционная система z/VM ОС z/VM [21, 24, 42] (последняя версия - V4R2) является высокопроизводительной многопользовательской интерактивной ОС, предоставляющей уникальные возможности в части выполнения различных операционных сред на одном ...
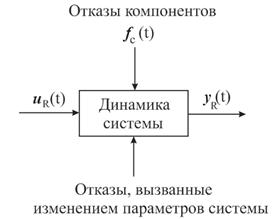
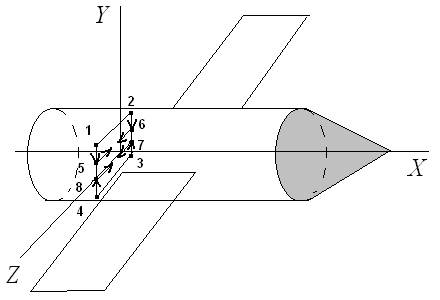
... , может приводить к большим потерям рабочего тела и раскрутке космического аппарата до недопустимых угловых скоростей. Таким образом разработка алгоритмов контроля и диагностики системы управления ориентацией космического аппарата – является актуальной задачей. В настоящей работе решается задача построения алгоритмов контроля и идентификации отказов командных приборов и исполнительных органов. ...
0 комментариев