Направление на траектории. Изменение параметризации

7. Направление на траектории. Изменение параметризации

Пусть L — траектория системы (I) и

х =  (t), y =  (t)

— какое-нибудь соответствующее ей решение.

Мы введем на траектории L определенное направление в качестве положительного. Именно, будем считать положительным направлением на L направление в сторону возрастания t. При таком определении можно сказать, что положительное направление в каждой точке траектории L совпадает с направлением вектора, заданного в этой точке системой (I).

Пользуясь «кинематической» интерпретацией, можно сказать, что положительное направление на L есть то направление, в котором точка с координатами х =  (t), y =  (t) движется по траектории при возрастании t и при котором направление ее скорости в каждой точке совпадает с направлением фазовой скорости.

Введенное таким образом положительное направление на L не зависит от того, какое из решений, соответствующих траектории L, мы возьмем (так как все такие решения получаются одно из другого заменой t на

В дальнейшем мы будем обычно опускать слово «положительное», т. е. под направлением на траектории L системы (I) мы будем подразумевать положительное направление, определяемое (или, как говорят, индуцируемое) на L этой системой.

Рассмотрим наряду с системой (I) систему

(I')

Векторное поле системы (I') получается из векторного поля системы (I), если изменить направление каждого вектора на противоположное (не меняя длин векторов).

Непосредственной проверкой устанавливается, что каждому решению

х =  (t), y =  (t) (23)

системы (I) соответствует решение

х =  (-t), y =  (-t) (24)

системы (I'). Отсюда очевидно, что системы (I) и (1') имеют одинаковые траектории, но индуцируют на траекториях противоположные направления. Таким образом, переход от системы (I) к системе (I') можно рассматривать, как изменение параметризации на траекториях, именно, как замену параметра t параметром —t.

Рассмотрим более общий случай изменения параметризации на траекториях системы (1). Пусть f (х, у) — функция класса C₁ , заданная в области G. Предположим, что функция f(х, у) отлична от нуля во всех точках области G, отличных от состояний равновесия системы (1), и имеет в них один и тот же знак.

Рассмотрим наряду с системой (I) систему

 (I*)

В силу предположений, сделанных относительно функции f(х, у), очевидно, что состояния равновесия системы (I) совпадают с состояниями равновесия системы (I*).

Лемма 8. Если

х =  (t), y =  (t) (25)

есть решение системы (I), причем соответствующая ему траектория отлична от состояния равновесия, то существует монотонная функция класса C₁ (t) = (s) такая, что пара функций

(26)

является решением системы (I*).

Доказательство. Задавая какое-нибудь начальное значение t₀, t₀(, Т), где (, Т) — интервал определения решения (25), и произвольное s₀, рассмотрим следующую функцию s(t)

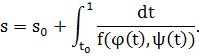
Так как f(х, у) не обращается в нуль в точках, отличных от состояний равновесия, то s(t) является монотонной функцией класса С₁ , определенной на интервале (, Т). Очевидно, существует обратная функция

(s), определенная в некотором интервале ( S), также класса С₁ , монотонная. Очевидно,

Поэтому

(27)

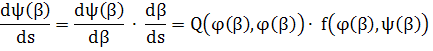
Последние соотношения показывают, что функции (26) являются решением системы (I*). Нетрудно видеть, что ( S), является максимальным интервалом определения решения (26), так как в противном случае интервал (, Т) не был бы максимальным для решения (25). Лемма доказана.

Уравнения (25) и (26) являются, очевидно, различными параметрическими уравнениями одной и той же траектории. Поэтому из леммы 8 следует, что динамические системы (I) и (I*) имеют одни и те же траектории, но с различными параметризациями на них. При переходе от системы (I) к системе (I*) направления на траекториях остаются неизменными, если f(х, у) > 0, и меняются, если F(x,y)<0.

Предположим теперь, что функция f(х, у) может обращаться в нуль в точках, отличных от состояний равновесия системы (I), а также может менять знак в области G. Рассмотрим снова систему (I*). Очевидно, состояниями равновесия системы (I*) являются все состояния равновесия системы (I), а также все точки области G, которые не являются состояниями равновесия системы (1), но в которых f(х, у) = 0.

Кривая f(х, у) = 0 называется особой линией системы (I*) (каждая точка этой кривой является состоянием равновесия системы (I*)).

Рассмотрим теперь траекторию L системы (I), отличную от состояния равновесия. Если на траектории L функция f(х, у) 0, то так же, как и выше, L является траекторией системы (I*) с измененной, вообще говоря, параметризацией.

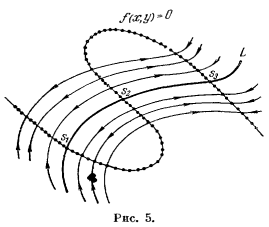
Если же на траектории L имеются точки кривой f(х, у) = 0, то все точки L, отличные от этих точек, распадаются, как легко видеть, на конечное или счетное число гладких кривых, являющихся траекториями системы (I*) (рис. 5). Направление на каждой такой траектории совпадает с направлением на L, если на этой траектории f(х, у) > 0, и не совпадает в противном случае.

Таким образом, каждая траектория системы (I) либо является траекторией системы (I*), либо состоит из конечного или бесконечного множества траекторий системы (I*) .

В дальнейшем, в ряде предложений и в примерах мы неоднократно будем встречаться с динамическими системами вида

 ()

где Р (х, у), Q (х, у) — функции класса C_N ( > 1) или аналитические, f(х, y) — функция класса C_N или аналитическая, которая может обращаться в нуль в области G (в которой рассматривается система). Очевидно, в точках, где (х, у) = 0, правые части рассматриваемой системы (I **) не определены. Однако при указанном виде правых частей можно путем замены параметра t привести рассмотрение системы (I**) к рассмотрению системы вида (I).

Действительно, полагая при х и у, необращающих в нуль f(х, у), dt =f(х, у) d, мы получаем систему

  (I***)

Эту же систему мы будем рассматривать при х и у, обращающих в нуль функцию f(х, у) (что соответствует доопределению по непрерывности), так что система (I***) будет определена во всей области G. Очевидно, во всякой части области G, в которой f(х, у) не обращается в нуль, траектории системы (I**) и (I***) совпадают как точечные множества, однако, параметры на них различны. При этом там, где f(х, у) > 0, направление по  совпадает с направлением по t, а там, где f(х, у) < 0 — противоположно ему. Точки с координатами х и у, обращающими в нуль функцию f(х, у), в которых правые части системы (I**) не определены, естественно выделять и считать не принадлежащими траекториям системы (I**) (к таким точкам, как нетрудно убедиться на простых примерах, точка по траектории может стремиться при t, стремящемся к конечному значению).

Похожие работы

Автоматизация системы бюджетирования финансовой службы

Скачать

568458

20

78

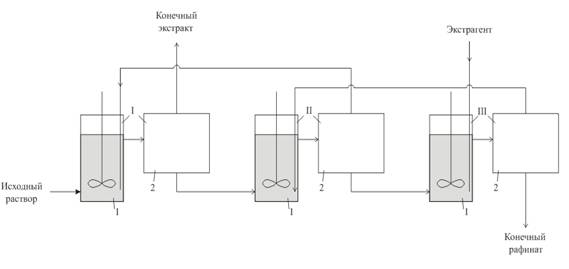
... для реализации системы бюджетирования Консультационной группы "Воронов и Максимов". Статья о проблемах выбора системы бюджетирования - в проекте "УПРАВЛЕНИЕ 3000". Бюджетный автомат Если вы решитесь на автоматизацию системы бюджетирования компании, перед вами сразу встанут вопросы: что выбрать, сколько платить, как внедрять. Примеряйте! О ЧЕМ РЕЧЬ В “Капитале” на стр. 44, 45 мы рассказали ...

Диагностика отказов системы регулирования уровня в баке

Скачать

135054

16

63

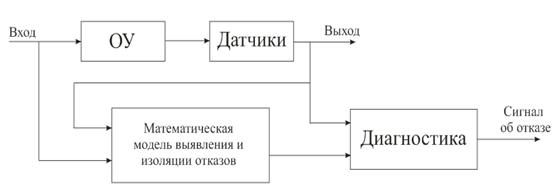
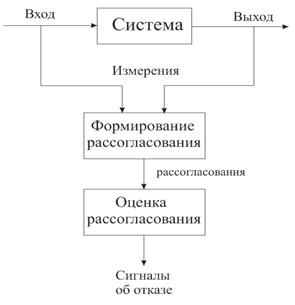
... сети могут быть использованы как классификаторы для разделения образцов рассогласований и формирования сигналов тревог. Таким образом, они могут выявлять и изолировать отказы. 3. Диагностика отказов системы регулирования уровня жидкости в баке   3.1. Постановка задачи Реализацию описанного выше метода диагностики отказов, основанного на моделях будем выполнять применительно к системе ...

Операционные системы "тонких" клиентов

Скачать

257667

0

26

... их интеграция, расширение их возможностей в новых версиях, создание новых средств и перенос их на другие аппаратные платформы и в другие ОС IBM. 12.4 Операционная система z/VM ОС z/VM [21, 24, 42] (последняя версия - V4R2) является высокопроизводительной многопользовательской интерактивной ОС, предоставляющей уникальные возможности в части выполнения различных операционных сред на одном ...

Разработка алгоритмов контроля и диагностики системы управления ориентацией космического аппарата

Скачать

175590

30

100

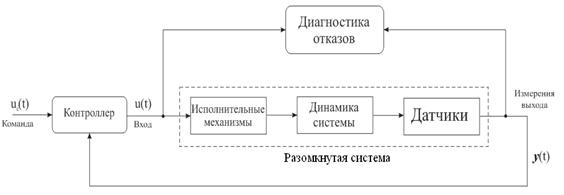
... , может приводить к большим потерям рабочего тела и раскрутке космического аппарата до недопустимых угловых скоростей. Таким образом разработка алгоритмов контроля и диагностики системы управления ориентацией космического аппарата – является актуальной задачей. В настоящей работе решается задача построения алгоритмов контроля и идентификации отказов командных приборов и исполнительных органов. ...