Простейшие свойства решений системы (I)
Геометрическая интерпретация динамической системы на фазовой плоскости (х, у)
Разбиение области в фазовой плоскости на траектории
Направление на траектории. Изменение параметризации
Терминология и обозначения
Теорема о непрерывной зависимости от начальных значений
Замена переменных
Изоклины
Примеры
Навигация
Теорема о непрерывной зависимости от начальных значений
Динамические системы в плоской области
75588
знаков
0
таблиц
20
изображений
9. Теорема о непрерывной зависимости от начальных значений
Наряду с теоремой о существовании и единственности решения основной теоремой теории дифференциальных уравнений является теорема о непрерывной зависимости от начальных значений.
Мы сформулируем здесь эту теорему для рассматриваемых нами автономных систем вида (I).
Теорема 4. Пусть
x=
(t — t0, х0, у0) , y = 
(t — t0, х0, у0)
— решение системы (I), определенное на интервале (
, Т), а 
и 
( < ) — два произвольных числа из этого интервала. Тогда, каково бы ни было 
> 0, существует такое 
> 0, что, если
то решение x = (t — t0, 
), y = (t — t0, ) определено при всех значениях t , 
t 
при всех этих значениях t выполняются неравенства
Замечание. Функции (t — t0, x0, y0), (t — t0, x0, y0) по самому своему определению являются непрерывными функциями t — t0.
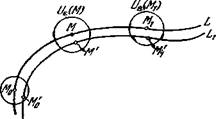
Рис. 6.
Так как в силу настоящей теоремы эти функции непрерывны по переменным х0, у0 и равномерно непрерывны относительно t на всяком замкнутом конечном промежутке значений t, то, очевидно, эти функции непрерывны по совокупности своих аргументов при всех тех значениях этих аргументов, при которых они определены.
Теорема 4 может быть также сформулирована в следующей геометрической форме, которой мы в основном будем пользоваться в дальнейшем.
Теорема 4'. Пусть
М0 (х0, у0) и M1 (x1 y1)
— две точки произвольной траектории L, соответствующие значениям t0 и t1 переменного t. Тогда для любого > 0 можно указать такое 
> 0, что если точка М'0
(М0), то проходящая через эту точку при t = t0 траектория L' определена для всех t в промежутке 
(или t0
) и точка М' траектории L', соответствующая любому значению t из этого промежутка, лежит в -окрестности точки М траектории L, соответствующей тому же t (рис. 6).
Докажем лемму, непосредственно вытекающую из теоремы 4.
Лемма 9. Пусть К — замкнутое ограниченное множество, целиком лежащее в G. Всегда существует h0 > 0 такое, что при любом t0 решение
x= (t — t0, x0, y0), y= (t — t0, x0, y0) (30)
для любой точки М0 (х0, у0) 
К заведомо определено при всех значениях t из промежутка
t0 - ht t0 +h.
Доказательство. Предположим, что лемма несправедлива, т. е. для любого h > 0 найдется такая точка М 
К, что решение (30), которое мы для краткости запишем в виде M = M(t — t0, 
), не определено на всем сегменте [t0 — h, t0 + h]. Тогда существует последовательность стремящихся к нулю положительных чисел { 
} и последовательность точек { 
} множества К таких, что решение M = M(t — t0, 
) не определено на всем сегменте [t0 — hn, t0 + hn]. Так как по предположению К — замкнутое ограниченное множество, то из { } всегда можно выбрать последовательность, сходящуюся к некоторой точке М* множества К. Поэтому мы можем без ограничения общности считать, что сама последовательность { } сходится к некоторой точке M* К. Рассмотрим решение M = M(t—t0, М*). Всегда существует h* > 0 такое, что это решение во всяком случае определено при значениях t на сегменте [t0—h*, t0 + h*]. В силу теоремы 4 тогда и всякое решение
M=M(t — t0, Mn)
при достаточно большом n определено на сегменте [t0 — h*, t0 + h*]. Ho hn < h* при достаточно большом n (так как hn
0), и, следовательно, решение М = М (t — t0, Mn) должно быть определено при всех значениях t из сегмента [t0 — hn, t0 + hn ], что противоречит выбору точек Мn. Лемма доказана.
Похожие работы
... для реализации системы бюджетирования Консультационной группы "Воронов и Максимов". Статья о проблемах выбора системы бюджетирования - в проекте "УПРАВЛЕНИЕ 3000". Бюджетный автомат Если вы решитесь на автоматизацию системы бюджетирования компании, перед вами сразу встанут вопросы: что выбрать, сколько платить, как внедрять. Примеряйте! О ЧЕМ РЕЧЬ В “Капитале” на стр. 44, 45 мы рассказали ...
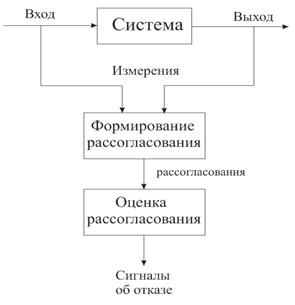
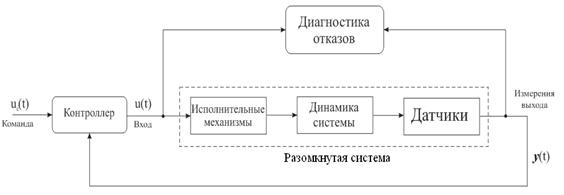
... сети могут быть использованы как классификаторы для разделения образцов рассогласований и формирования сигналов тревог. Таким образом, они могут выявлять и изолировать отказы. 3. Диагностика отказов системы регулирования уровня жидкости в баке 3.1. Постановка задачи Реализацию описанного выше метода диагностики отказов, основанного на моделях будем выполнять применительно к системе ...
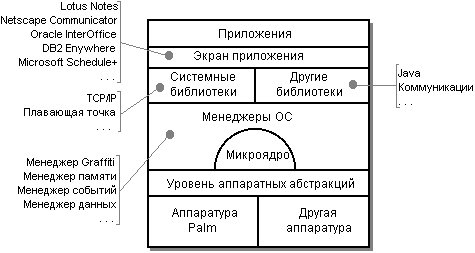
... их интеграция, расширение их возможностей в новых версиях, создание новых средств и перенос их на другие аппаратные платформы и в другие ОС IBM. 12.4 Операционная система z/VM ОС z/VM [21, 24, 42] (последняя версия - V4R2) является высокопроизводительной многопользовательской интерактивной ОС, предоставляющей уникальные возможности в части выполнения различных операционных сред на одном ...
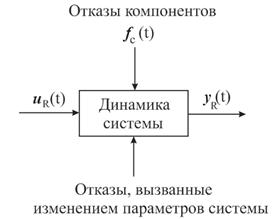
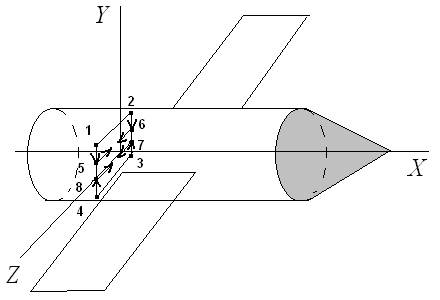
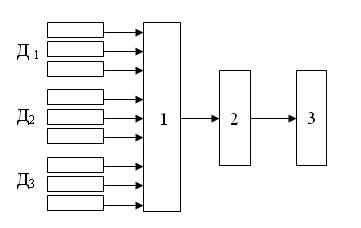
... , может приводить к большим потерям рабочего тела и раскрутке космического аппарата до недопустимых угловых скоростей. Таким образом разработка алгоритмов контроля и диагностики системы управления ориентацией космического аппарата – является актуальной задачей. В настоящей работе решается задача построения алгоритмов контроля и идентификации отказов командных приборов и исполнительных органов. ...
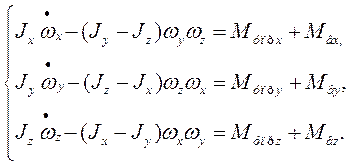
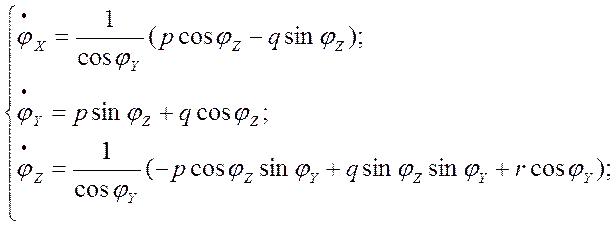
0 комментариев