Простейшие свойства решений системы (I)
Геометрическая интерпретация динамической системы на фазовой плоскости (х, у)
Разбиение области в фазовой плоскости на траектории
Направление на траектории. Изменение параметризации
Терминология и обозначения
Теорема о непрерывной зависимости от начальных значений
Замена переменных
Изоклины
Примеры
Навигация
Изоклины
Динамические системы в плоской области
75588
знаков
0
таблиц
20
изображений
12. Изоклины
Кривые, расположенные в области G и имеющие уравнение
Q(x, у) 
С 
Р (х, у) = 0 (34)
(С — постоянное) или уравнение
Р(x, y) = 0, (35)
называются изоклинами (линиями равного наклона) системы (I) или уравнения (III). Эти кривые обладают, очевидно, тем свойством, что траектории системы (I), проходящие через все отличные от состояний равновесия точки каждой кривой, имеют в этих точках одинаковые направления касательных. Именно, угловые коэффициенты траекторий в точках изоклины (34) равны С, а в точках изоклины (35) равны 
. Таким образом, направление касательной к траектории меняется только при переходе точки с одной изоклины на другую.
Изоклины Q (х, у) = О и Р (х, у) = 0 называются главными изоклинами. В точках первой из них касательные к траекториям горизонтальны, а в точках второй — вертикальны. Поэтому главные изоклины называют также изоклинами горизонтальных, соответственно вертикальных, наклонов.
Очевидно, все состояния равновесия лежат на каждой из изоклин и, обратно, общие точки любых двух изоклин (различных) являются состояниями равновесия системы. В частности, состояния равновесия являются общими точками двух главных изоклин.
13. Понятия «интеграл», «интегральная кривая», «общий интеграл». использующиеся в классической литературе при рассмотрении аналитических систем
В этом пункте мы введем понятия «интеграл», «интегральная кривая», «общий интеграл» дифференциального уравнения или системы уравнений так, как это обычно делается в классической литературе при рассмотрении аналитических дифференциальных уравнений и систем.
Мы останавливаемся здесь на указанных понятиях, не играющих роли в излагаемой дальше теории ввиду того, что они часто используются в дальнейшем при рассмотрении примеров.
Пусть рассматриваемая система (I)
Р(х, у) 
Q(x, у)
является аналитической в области G. Соответствующее этой системе дифференциальное уравнение запишем в симметричной форме (III)
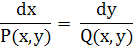
интеграл динамический плоскость траектория
Пусть функция F (х, у) удовлетворяет следующим условиям:
а) она является аналитической во всех точках кривой, заданной соотношением
F(x,y) = 0, (36)
б) во всех точках кривой (36) тождественно выполняется равенство
(х, у) Р(х, y) + 
(x, y)Q(x, y)=0. (37)
Тогда соотношение (36) называется интегралом или частным интегралом уравнения (III) или системы (I), а кривая, определяемая этим соотношением, интегральной кривой уравнения (III) или системы (I).
Пусть F (х, у) = 0 — интеграл системы (I). Рассмотрим соответствующую интегральную кривую. Эта кривая может иметь в числе своих точек состояния равновесия системы (I), а также точки, в которых одновременно F'x (х, у) = F'y (х, у) = 0, т. е. особые точки кривой (36).
Покажем, что всякий “кусок” интегральной кривой, не содержащий состояний равновесия системы (I) и не имеющий особых точек, является траекторией системы (I) или представляет часть такой траектории.
В самом деле, рассмотрим произвольную точку М0 (х0, ус) такого куска кривой (36). Предположим, что в этой точке
F'y (x0, у0) 
0
Тогда в некоторой окрестности точки М0 кривая может быть задана уравнением вида y = f(x), причём
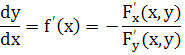
для всех точек кривой в этой окрестности. Так как F'y (х0, у0) 0, то в окрестности точки М0 , F'y (x, у) также отлична от нуля. Из соотношения (37)
F'x(x, y)P(x, y) + F'y(x, y)Q(x,y)=0
следует, что Р (х, у) 0 в окрестности точки М0 и что
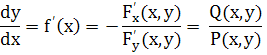
Но это значит, что функция y = f(x) удовлетворяет уравнению (II)
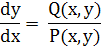
Аналогично рассматривается случай, когда F'x (x0, у0) 0. Таким образом, рассматриваемый кусок кривой (36) является куском интегральной кривой в смысле п. 11, т. е. представляет траекторию или часть траектории системы (I).
Рассмотрим теперь семейство кривых
F{x% у, С) = 0, (38)
определенное для значений С в некоторой области (обычно в некотором интервале).Соотношение (38) называется общим интегралом уравнения (III) или системы (1), если каждая кривая семейства (38) является интегральной кривой в определенном выше смысле и если каждая точка области G принадлежит по крайней мере одной из кривых (38).
Из этого определения следует, в частности, что если некоторая функция Ф (х, у) определена в области G и является аналитической во всех точках этой области, за исключением, быть может, состояний равновесия системы (I), и удовлетворяет в области тождеству
Ф'х(х, у)Р(х, у) + Ф'y (х, y)Q(x, y) 
0, то соотношение
Ф(x, y) = С (39)
является общим интегралом системы (I).
Если у системы (I) (или уравнения (III) существует общий интеграл вида (39), причем Ф (x, у) есть функция, аналитическая во всех точках области G, то, говорят, что система (I) (или уравнение (III)) имеет в области G аналитический интеграл . В частности, системами вида (I), имеющими аналитический интеграл, являются так называемые гамильтоновы системы, о которых уже говорилось во введении
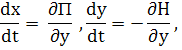
где Н (x, у) — аналитическая функция. H (х, у) = С является аналитическим интегралом (так называемым «интегралом энергии») этой системы.
Знание аналитического интеграла системы (I) в некоторых частных случаях помогает проводить качественное исследование системы (I).
Похожие работы
... для реализации системы бюджетирования Консультационной группы "Воронов и Максимов". Статья о проблемах выбора системы бюджетирования - в проекте "УПРАВЛЕНИЕ 3000". Бюджетный автомат Если вы решитесь на автоматизацию системы бюджетирования компании, перед вами сразу встанут вопросы: что выбрать, сколько платить, как внедрять. Примеряйте! О ЧЕМ РЕЧЬ В “Капитале” на стр. 44, 45 мы рассказали ...
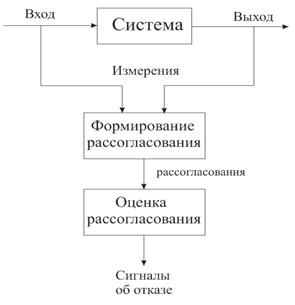
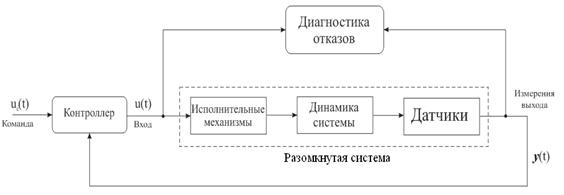
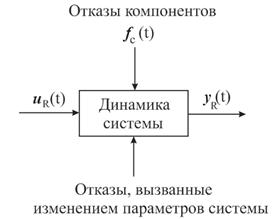
... сети могут быть использованы как классификаторы для разделения образцов рассогласований и формирования сигналов тревог. Таким образом, они могут выявлять и изолировать отказы. 3. Диагностика отказов системы регулирования уровня жидкости в баке 3.1. Постановка задачи Реализацию описанного выше метода диагностики отказов, основанного на моделях будем выполнять применительно к системе ...
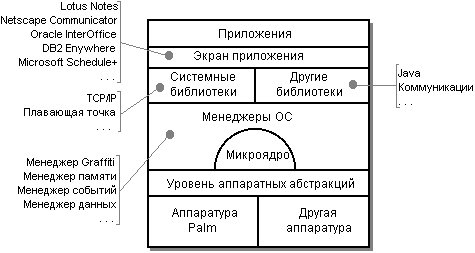
... их интеграция, расширение их возможностей в новых версиях, создание новых средств и перенос их на другие аппаратные платформы и в другие ОС IBM. 12.4 Операционная система z/VM ОС z/VM [21, 24, 42] (последняя версия - V4R2) является высокопроизводительной многопользовательской интерактивной ОС, предоставляющей уникальные возможности в части выполнения различных операционных сред на одном ...
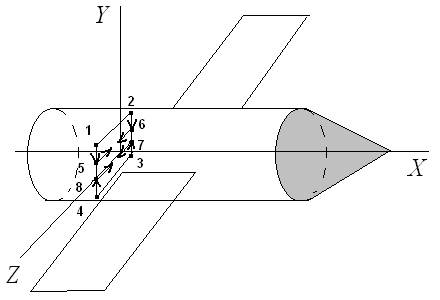
... , может приводить к большим потерям рабочего тела и раскрутке космического аппарата до недопустимых угловых скоростей. Таким образом разработка алгоритмов контроля и диагностики системы управления ориентацией космического аппарата – является актуальной задачей. В настоящей работе решается задача построения алгоритмов контроля и идентификации отказов командных приборов и исполнительных органов. ...
0 комментариев