Навигация
Оптимальность управления и достаточность системы ограничений
2.4. Оптимальность управления и достаточность системы ограничений.
В экономических системах (моделях) критерием оптимальности выбирают параметры, как правило, определяющие наилучшим образом эффективность данной системы. Такими параметрами могут быть максимальная прибыль и затраты, минимальное время достижения цели и т.д.
Вектор оптимального управления – набор тех параметров, которые обеспечивают оптимальную траекторию функционирования данной ЭС. В любой модели (ЭС) имеются ограничения по ресурсам, по фондам и т.д. Поэтому система ограничений W – запись условий в виде уравнений, неравенств, в которых существует единственное оптимальное решение. Совместимость ограничений – обязательное условие разрешимости любой модели. На практике – это запасы ресурсов, сырья, трудовые ресурсы, финансовые ресурсы, др.
“Смягчить ограничение” - значит, получить показатель оптимизации оптимистичным.
“Ужесточить ограничения” - сделать более строгими, значит получить показатель оптимизации пессимистичным.
Ограничения могут встречаться в разных комбинациях.
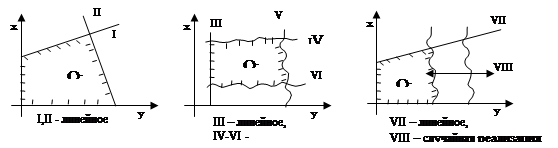
![]() ЭММ линейна тогда и только тогда, когда целевая функция и система ограничений линейны. Любая комбинация:
ЭММ линейна тогда и только тогда, когда целевая функция и система ограничений линейны. Любая комбинация:
- целевая функция линейна - W нелинейна;
- целевая функция нелинейна - W линейна;
- целевая функция нелинейна - W нелинейна;
приводит к нелинейности модели.
2.5. Формальная классификация моделей.
| Признак классификации | Модель |
| 1. Целевое назначение | Прикладные, теоретико-аналитические |
| 2. По типу связей | Детерминированные, стохастические |
| 3. По фактору времени | Статические, динамические |
| 4. По форме показателей | Линейные, нелинейные |
| 5. По соотношению экзогенных и эндогенных переменных | Открытые, закрытые |
| 6. По типу переменных | Дискретные, непрерывные, смешанные |
| 7. По степени детализации | Агрегированные (макромодели), детализированные (микромодели) |
| 8. По количеству связей | Одноэтапные, многоэтапные |
| 9. По форме представления информации | Матричные, сетевые |
| 10. По форме процесса | Аналитические, графические, логические |
| 11. По типу математического аппарата | Балансовые, статистические, оптимизационные, имитационные, смешанные |
Тема 3. Матричные ЭММ. Модель межотраслевого баланса.
3.1. Основные соотношения и понятия модели.
Матричные экономико-математические модели предназначены для анализа и планирования производства и распределения продукции на различных уровнях — от отдельного предприятия до народного хозяйства в целом.
Положительными и ценными качествами данной модели являются общность расчетов, которые опираются на знание коэффициентов прямых и полных материальных затрат.
Основу баланса составляет совокупность всех отраслей материального производства; их число равно п. Каждая отрасль дважды фигурирует в балансе: как производящая и как потребляющая. Отрасли как производителю продукции соответствует определенная строка, а отрасли как потребителю продукции — определенный столбец.
Если номер любой производящей отрасли обозначить через i, а номер любой потребляющей отрасли — через j, то находящиеся на пересечении отраслей (т. е. соответственно строк и столбцов) величины хij нужно понимать как стоимость средств производства, произведенных в i-й отрасли и потребленных в качестве материальных затрат в j-и отрасли.
хij – технологический коэффициент.
Матричная модель межотраслевого баланса
| Производящая отрасль | Потребляющая отрасль | Продукция, тыс.грн. | |||||
| 1 | 2 | 3 | j | N | Конечная | Валовая | |
| 1 | x11 | x12 | x13 | … | x1n | y1 | X1 |
| 2 | x21 | x22 | x23 | … | x2n | y2 | X2 |
| 3 | x31 | x32 | x33 | … | x3n | y3 | X3 |
| I | … | … | … | … | … | ... | … |
| N | xn1 | xn2 | xn3 | … | xnn | yn | Xn |
| Оплата труда | v1 | v2 | v3 | … | vn | vкон | - |
| Чистый доход, тыс. грн. | m1 | m2 | m3 | … | mn | mкон | - |
| Валовая продукция, тыс. грн. | X1 | X2` | X3 | … | Xn | - | X |
В столбцах межотраслевого баланса отражается структура материальных затрат и чистой продукции каждой отрасли. Допустим, 1-я отрасль—это производство электроэнергии, 2-я — угольная промышленность. Тогда величина х11 показывает стоимость электроэнергии, израсходованной внутри 1-й отрасли для собственных производственных нужд. Величина x12 отражает затраты угля в производстве электроэнергии. В целом же столбец х11, x21, х31, ..., хn1 характеризует структуру материальных затрат 1-й отрасли за отчетный год в разрезе отраслей-поставщиков.
В балансе отражены не только материальные затраты, но и чистая продукция отраслей. Так, чистая продукция 1-й отрасли характеризуется суммой оплаты труда v1 и чистого дохода (прибыли) m1. Итог материальных затрат и чистой продукции равен, очевидно, валовой продукции отрасли (например, для 1-й отрасли—величине Х1). Таким образом, можно записать:
Х1=х11+х21+х31+…+хn1+v1+m1 = ![]() (1)
(1)
То же соотношение для любой отрасли имеет следующий вид :
X![]() (2)
(2)
Если рассматривать модель по строкам межотраслевого баланса, то здесь представлено распределение годового объема продукции каждой отрасли материального производства
Х1 = х11+х12+х13+ … +х1т+y1 = ![]()
тогда для любой производящей отрасли
Хi= ![]() (3)
(3)
Если сравнить правую и левую части уравнений (2) и (3), то можно отметить, что у них присутствует общий член хij .Тогда можно записать выражение:
![]() (4)
(4)
Выражение (4) показывает, что в межотраслевом балансе собдюдается важнейший принцип – это единство материального баланса, представленного выражением, как единства вещественного и стоимостного состава национального дохода.
Квадрант I – промежуточная продукция, показывает распределение материальных затрат по всем производящим отраслям.
Квадрант II – конечная продукция, которая вышла из сферы производства и попала в сферу сбыта. В развернутом виде ее можно представить как продукцию, идущую на личное потребление, на общественные нужды, а также на восполнение ресурсов и экспорт.
Квадрант III – характеризует национальный доход со стороны его стоимостного состава как сумму оплаты труда и чистого дохода всех отраслей материального производства. Данные этого квадранта необходимы для глубокого экономического анализа.
Квадрант IV – отражение конечного распределения и использования национального дохода. Он находится на пересечении столбцов конечной продукции и строк национального дохода.
В целом модель отражает балансы отраслей материального производства, баланс всего общественного продукта, балансы национального дохода, финансовый баланс, баланс доходов и расходов населения. В балансе отражено единство материально-вещественного и стоимостного состава национального дохода.
Похожие работы
... отрезка времени. Как правило, это задача, решение которой влечет за собой постановки близких или аналогичных задач. Глава 2. Экономико-математическое моделирования процессов принятия управленческих решений. В классификации решений по времени действия выражается принцип их цикличности, определенная хронологическая последовательность, временные рамки которой неизбежно должны учитываться в процессе ...
... производственной функции, моделей поведения фирмы, моделей общего экономического равновесия, прежде всего модели Л. Вальраса и ее модификаций. Глава 2. История развития экономико-математического моделирования в США Для характеристики математического направления в экономике за последние 80 – 90 лет приведу лишь некоторые результаты, сыгравшие заметную роль в его развитии. Как в теоретическом, ...
... вопросы должны быть получены в ходе маркетинговых и проектно-изыскательских работ на фазе проектирования спортивных сооружений. И уже на этой стадии в процесс активно включаются экономико-математические методы, задействуется существующий аппарат математического моделирования и прогнозирования. Данные методы и расчеты совершенно необходимы для определения: сроков окупаемости отдельных предприятии ...
... <= 2,10 В разделе 1 проекта требуется: 1. Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала. Нужно формулировать экономико-математическую модель общей задачи линейного программирования (ОЗЛП); 2. С помощью полученных в результате реализации модели отчетов сделать рекомендации филиалу фирмы по расширению программы ...
0 комментариев