Навигация
ЭММ оптимизации производственного плана отрасли
4.2. ЭММ оптимизации производственного плана отрасли.
![]()
|
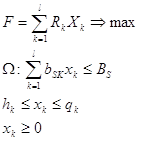
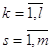 (13)
(13) k – вид, номер производимой продукции;
l – число видов продукции;
s – вид выделяемых ресурсов;
m – число видов выделяемых ресурсов;
Rk – прибыль от реализации единицы продукции k вида;
Xk - объем (количество изделий) k вида;
вsk – норма потребления S вида ресурсов при производстве единицы k вида продукции;
Bs – объем выделяемых ресурсов S вида ;
hk, qk – верхняя и нижняя граница, соответствующая по производству k вида продукции.
4.3. ЭММ оптимизации выпуска продукции предприятиями отрасли.
![]()
![]()
|
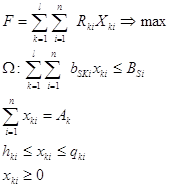
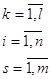 (14)
(14) i – номер предприятия;
n – число предприятий;
k – вид, номер производимой продукции;
l – число видов продукции;
s – вид выделяемых ресурсов;
m – число видов выделяемых ресурсов;
Rki – прибыль от реализации единицы продукции k вида на i предприятии;
Xki - объем (количество изделий) k вида на i предприятии;
Ak - план выпуска k вида продукции;
вski – норма потребления S вида ресурсов при производстве единицы k вида продукции на на i предприятии;
Bsi – объем выделяемых ресурсов S вида на i предприятии;
hki, qki – верхняя и нижняя граница, соответствующие производству k вида продукции на i предприятии.
4.4. ЭММ распределения финансовых ресурсов по оптимизации прироста мощностей (отрасли, предприятия, ...).
![]()
![]()
|
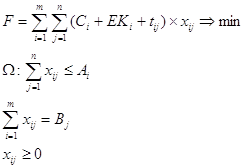
Сi – стоимость единицы продукции i поставщика;
Ki – капитальные затраты на единицу готовой продукции при строительстве нового предприятия;
E – нормирующий коэффициент эффективности капитальных вложений;
tij – транспортные расходы по перевозке единицы продукции i поставщика j потребителю;
xij – объем поставок продукции i поставщика j потребителю;
Ai – мощность i поставщика;
Bj – спрос j потребителя.
4.5. Распределение капитальных вложений по проектам.
![]()
![]()
|
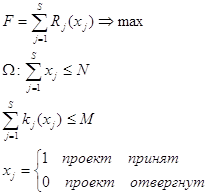
j – вариант (индекс) проекта капитальных вложений;
s – общее число проектов;
kj – объем капитальных вложений по j варианту;
M – суммарный годовой объем капитальных вложений;
Rj – ожидаемый доход от реализации j варианта капитальных вложений;
N – общее число вариантов капитальных вложений.
4.6. ЭММ составления оптимальных смесей, сплавов, соединений и выбор оптимального рациона питания (кормления).
Данная модель позволяет исходя из стоимости исходных компонентов и содержания необходимых элементов в исходных компонентах получить дешевый выходной продукт. Данная модель применяется на металлургических, химических, нефтеперерабатывающих заводах, крупных АПК.
![]()
![]()
|
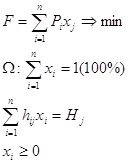
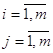 (17)
(17) i – номер (индекс) исходного материала;
n – количество исходных компонентов;
j – номер (индекс) химического элемента;
m – общее количество компонентов, входящих в готовую продукцию;
hij - %(доля) j химического элемента в i исходном материале;
Hj - %(доля) j химического элемента готовой продукции;
Pi – цена за единицу каждого i исходного материала;
Xi - % (доля) i исходных материалов.
Похожие работы
... отрезка времени. Как правило, это задача, решение которой влечет за собой постановки близких или аналогичных задач. Глава 2. Экономико-математическое моделирования процессов принятия управленческих решений. В классификации решений по времени действия выражается принцип их цикличности, определенная хронологическая последовательность, временные рамки которой неизбежно должны учитываться в процессе ...
... производственной функции, моделей поведения фирмы, моделей общего экономического равновесия, прежде всего модели Л. Вальраса и ее модификаций. Глава 2. История развития экономико-математического моделирования в США Для характеристики математического направления в экономике за последние 80 – 90 лет приведу лишь некоторые результаты, сыгравшие заметную роль в его развитии. Как в теоретическом, ...
... вопросы должны быть получены в ходе маркетинговых и проектно-изыскательских работ на фазе проектирования спортивных сооружений. И уже на этой стадии в процесс активно включаются экономико-математические методы, задействуется существующий аппарат математического моделирования и прогнозирования. Данные методы и расчеты совершенно необходимы для определения: сроков окупаемости отдельных предприятии ...
... <= 2,10 В разделе 1 проекта требуется: 1. Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала. Нужно формулировать экономико-математическую модель общей задачи линейного программирования (ОЗЛП); 2. С помощью полученных в результате реализации модели отчетов сделать рекомендации филиалу фирмы по расширению программы ...
0 комментариев