Навигация
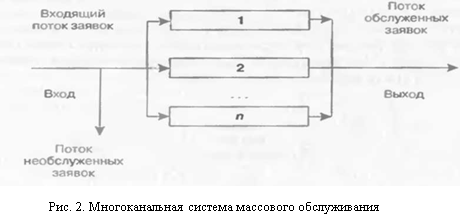
Имитационная модель и ее структура
5.3. Имитационная модель и ее структура..

При создании модели необходимо максимально использовать те параметры системы, которые поддаются формализации, то есть записи с помощью аналитических выражений.
5.4. Метод Монте-Карло (метод статистических испытаний).
Данный метод родился в 1949 году благодаря усилиям американских ученых Дж. Неймана и Стива Улана в городе Монте-Карло (княжество Монако).
Метод Монте-Карло – численный метод решения математических задач при помощи моделирования случайных чисел.
Суть метода состоит в том, что посредствам специальной программы на ЭВМ вырабатывается последовательность псевдослучайных чисел с равномерным законом распределения от 0 до1. Затем данные числа с помощью специальных программ преобразуются в числа, распределенные по закону Эрланга, Пуассона, Релея и т.д.
Полученные таким образом случайные числа используются в качестве входных параметров экономических систем :
Q (x1, x2, x3,…,xn) Þ Qpt (min или max)
 W: Bs (x1, x2, x3,…,xn) £ Rs
W: Bs (x1, x2, x3,…,xn) £ Rs
При многократном моделировании случайных чисел, которые мы используем в качестве входных параметров системы (модели), определяем математическое ожидание функции M(Q) и, при достижении средним значением функции Q уравнения не ниже заданного, прекращаем моделирование.
Статистические испытания (метод Монте-Карло) характеризуются основными параметрами:
D - заданная точность моделирования;
P – вероятность достижения заданной точности;
N – количество необходимых испытаний для получения заданной точности с заданной вероятностью.
Определим необходимое число реализаций N, тогда
(1 - D) будет вероятность того, что при одном испытании результат не достигает заданной точности D;
(1 - D) N – вероятность того, что при N испытаниях мы не получим заданной точности D.
Тогда вероятность получения заданной точности при N испытаниях можно найти по формуле
![]() (19)
(19)
Формула (19) позволяет определить заданное число испытаний для достижения заданной точности D с заданной вероятностью Р.
| D | Значение Р | |||
| 0,80 | 0,20 | 0,95 | 0,99 | |
| 0,10 0,05 0,025 0,0125 0,006 | 16 32 64 161 322 | 22 45 91 230 460 | 29 59 116 299 598 | 44 90 182 459 919 |
êQi – Qконеч êÞ D
Случайные числа получаются в ЭВМ с помощью специальных математических программ или спомощью физических датчиков. Одним из принципов получения случайных чисел является алгоритм Неймана, когда из одного случайного числа последовательно выбирается середина квадрата
g0 = 0,9876 g0 2 = 0,97531376
g1 = 0,5313 g12= 0,28654609
g2 = 0,6546 g22= 0,42850116 и т.д.
Кроме того данные числа проверяются на случайность и полученные числа заносятся в базу данных.
Физические датчики разрабатываются на электронных схемах и представляют собой генераторы белого (нормального) шума, то есть когда в спектральном составе шума имеются гармоничные составляющие с частотой F ®¥. Из данного белого шума методом преобразования получаются случайные числа.
Тема 6. Методы и модели управления запасами.
6.1. Основные определения и понятия теории управления запасами.
Любая СЭС, как и техническая система, может ритмично работать при наличии достаточного запаса ресурсов.
В качестве ресурсов для обеспечения ритмичного производства используются:
- материальные ресурсы (сырье, полуфабрикаты, энергоносители);
- технологические, трудовые ресурсы;
- финансовые и другие ресурсы.
Ритмичность поставок вынуждают следующие обстоятельства:
1) несовпадение ритмов производства с ритмами потребления;
2) случайные колебания спроса за период между поставками;
3) случайные колебания интервала между поставками;
4) срыв объема поставок.
То есть появляется случайная составляющая в целевой функции оптимизации эффективности производства.
Предпосылки, которые заставляют оптимизировать запасы сырья, ресурсов:
1) возрастают убытки за счет хранения сверхнормативных запасов;
2) связывание оборотных средств;
3) потеря в качестве материальных ресурсов, моральное и физическое старение ресурсов.
В качестве целевой функции в задачах управления запасами выступают суммарные затраты на:
1) приобретение продукции с учетом максимальных скидок на размер партии;
2) затраты на хранение и складские операции;
3) от материального и морального старения при хранении;
4) потери от дефицита и штрафных санкций.
Целевая функция, представляющая сумму данных компонентов, должна быть min. Поэтому управление запасами производится в начале путем выбора стратегии в пространствестратегий управления, а затем путем выбора параметров в прострастве параметров управления.
Запасы делятся на:
1) текущие (обеспечивают ритм производства на определенном интервале времени);
2) страховые (на случай срыва ритма поставок).
Из параметров управления запасами принято выделять:
1) управляемые параметры
- объем и номенклатура необходимого сырья (ресурсов);
- момент (время) выдачи заказа на пополнение ресурса;
2) неуправляемые параметры
- затраты на организацию снабжения;
- ограничение на запасы поставщика;
- выбор системы снабжения (централизованная, децентрализованная)
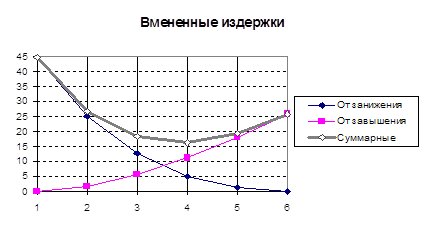
Качественно систему снабжения можно представить графически:
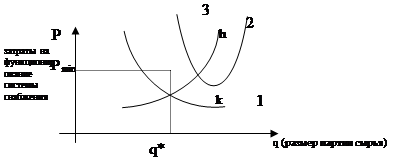
Р – затраты на функционирование системы снабжения;
1 – затраты на размещение заказов;
2 – затраты на хранение данных ресурсов;
3- суммарные затраты на функционирование системы снабжения;
q* - оптимальный размер (объем) заказа сырья.
6.2. Классификация систем снабжения и их моделей.
| Признак | Тип модели | |
| I | По типу системы снабжения | 1. эшелонированные (многоэтапные) 2. децентрализованные |
| II | По числу хранимого сырья | 1. многокомпонентные 2. однокомпонентные |
| III | По спросу | 1. детерминированная: · дискретная · непрерывная 2. случайная (вероятностная): · дискретная · непрерывная |
| IV | По способу поставки сырья | 1. мгновенная 2. с фиксированным временем задержки 3. со случайным временем задержки |
| V | По видам затрат и способам их отражения в модели | 1. линейная 2. нелинейная |
| VI | По ограничениям системы снабжения | 1. по объему 2. по весу 3. по площади 4. по себестоимости 5. по числу поставщиков |
| VII | По принятой стратегии управления | 1. периодические (с периодом контроля Т) 2. по критическим уровням и объему. Н – верхний уровень; n – нижний уровень запасов; q – объем партии (поставок). |
6.3. Стратегия управления запасами.
Оптимальное управление запасами – выбор таких объемов и моментов поставок, когда суммарные издержки на функционирование системы снабжения будут минимальными.
Простейшие стратегии:
1) периодические (со временем контроля Т);
2) по критическим уровням (H, h, yi – текущий уровень запаса q).
1. Стратегия постоянного уровня.
В данном случае через каждый интервал контроля Т запас пополняется до верхнего уровня.
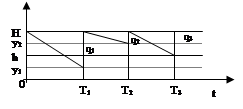 q1 ¹ q2 ¹ q3 ¹ const
q1 ¹ q2 ¹ q3 ¹ const
q* опт = H – yтек
y1,2 – текущие уровни
2. Стратегия фиксированного объема поставок.
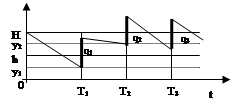
Q* = const
q1 = q2 = q3 = const
3. Стратегия с контролем за текущим уровнем.
a) если y < h, то: - y < h Þ q* = const
- y ³ h Þ q* = 0 (не заказываем сырье)
b) если y < h, то: - y < h Þ q* = H – yтек
- y ³ h Þ q* = 0
6.4. Детерминированная ЭММ управления запасами с фиксированным спросом.
Данная модель называется моделью экономики выгодных размеров поставок.
Начальные условия (ограничения):
1. Известны моменты поступления заявок.
2. Интенсивность расходования ресурсов (скорость).
3. Поставки мгновенны.
4. Отсутствие дефицита.
Введем обозначения:
b - интенсивность спроса;
k – затраты на оформление;
h – затраты на хранение единицы продукции в единицу времени;
q – объем поставок (размер партии сырья).
![]() - период времени, в течение которого полностью расходуется сырье.
- период времени, в течение которого полностью расходуется сырье.
F(q) – суммарные затраты на функционирование системы снабжения
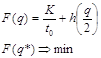
q/2 – оптимизация ведется по среднему уровню;
q* - оптимальный размер заказа.
Для нахождения F* нужно взять частную производную целевой функции F(q) по оптимизационному параметру q.
![]()
Из данной формулы находим q*:
![]() формула Уилсона (оптимального заказа).
формула Уилсона (оптимального заказа).
Данный заказ необходимо разместить для выполнения через время
![]()
Оптимальные затраты можно определить по формуле
![]() - это затраты на единицу продукции.
- это затраты на единицу продукции.
Похожие работы
... отрезка времени. Как правило, это задача, решение которой влечет за собой постановки близких или аналогичных задач. Глава 2. Экономико-математическое моделирования процессов принятия управленческих решений. В классификации решений по времени действия выражается принцип их цикличности, определенная хронологическая последовательность, временные рамки которой неизбежно должны учитываться в процессе ...
... производственной функции, моделей поведения фирмы, моделей общего экономического равновесия, прежде всего модели Л. Вальраса и ее модификаций. Глава 2. История развития экономико-математического моделирования в США Для характеристики математического направления в экономике за последние 80 – 90 лет приведу лишь некоторые результаты, сыгравшие заметную роль в его развитии. Как в теоретическом, ...
... вопросы должны быть получены в ходе маркетинговых и проектно-изыскательских работ на фазе проектирования спортивных сооружений. И уже на этой стадии в процесс активно включаются экономико-математические методы, задействуется существующий аппарат математического моделирования и прогнозирования. Данные методы и расчеты совершенно необходимы для определения: сроков окупаемости отдельных предприятии ...
... <= 2,10 В разделе 1 проекта требуется: 1. Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала. Нужно формулировать экономико-математическую модель общей задачи линейного программирования (ОЗЛП); 2. С помощью полученных в результате реализации модели отчетов сделать рекомендации филиалу фирмы по расширению программы ...
0 комментариев