Навигация
ЭММ оптимизации раскроя материала
4.7. ЭММ оптимизации раскроя материала.
Данная модель позволяет выбирая один из способов раскроя, изготовить определенное количество заготовок с минимальным расходом материала.
![]()
![]()
|
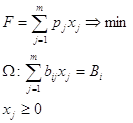
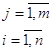 (18)
(18) i – номер (вид) заготовки;
n – общее количество разновидностей заготовок;
j – способ раскроя;
m – общее количество способов раскроя;
bij – количество выкраиваемых заготовок;
Вi – количество штук заготовок i вида;
Xj – количество исходного материала, который необходимо раскроить j способом;
Pj- величина отходов при данном j-м способе раскроя.
4.8. Экономическая интерпретация двойственных задач линейного программирования.
При моделировании экономических систем и процессов, когда характер системы до конца не изучен, или же система сложная, прибегают к упрощению модели и представлению ее в виде линейной (прямой или обратной).
Исходная модель предполагает, сколько и какой продукции необходимо изготовить с заданной стоимостью cj(j=![]() ) и при заданных ресурсах bi(i=
) и при заданных ресурсах bi(i=![]() )
и получить максимальную прибыль в стоимостном выражении.
)
и получить максимальную прибыль в стоимостном выражении.
Двойственная (обратная) задача предполагает оценку стоимости единицы каждого из ресурсов, чтобы при заданном количестве ресурсов bi и стоимости единицы продукции cjминимизировать общую стоимость затрат.
|
|
Тема 5. Методы моделирования стохастических (вероятностных) систем. Имитационное моделирование.
5.1. Понятие о вероятностных системах и процессах.
Экономические системы, как правило, являются вероятностными (стохастическими), так как выходные параметры системы случайным образом зависят от входных параметров.
Почему экономические системы являются стохастическими:
1) так как система сложная, многокритериальная многоуровневая иерархическая структура;
2) система подвержена влиянию внешних факторов (погодные условия, внешняя политика);
3) преднамеренное искажение информации, сокрытие информации и целенаправленная экономическая диверсия.
Исходя из того, что экономическая система сложная и имеет случайную компоненту e,
![]()
поэтому оптимизация целевой функции ведется по среднему значению, то есть при заданных параметрах a необходимо найти решение хÎC, когда значение целевой функции по возможности будет максимальным.
Сложные системы описываются Марковским аппаратом, то есть когда поведение системы в момент t0 характеризуется вероятностью первого порядка p(х0, t0) и поведение системы в будущем зависит от значения системы х0 и не зависит от того, когда и как система пришла в это состояние.
Марковские случайные процессы описываются двумя параметрами:
1) вероятностью первого порядка p(х0, t0);
2) условной вероятностью pij (х2 t2 /х1 t1);
pijхарактеризует значение системы х2 в момент t2, при условии, что в момент t1 система имела значение х1.
Имея в своем распоряжении матрицу условных переходов
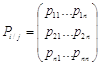
можно заранее сформулировать поведение системы в будущем.
Марковские случайные процессы называют Марковскими цепями с вероятностью перехода в pij, когда процесс изучается в дискретные моменты времени.
5.2. Имитационное моделирование систем и процессов.
Применяется в случаях, когда нельзя заформализовать модель (описать аналитическим выражением) и в случае, когда система представляет собой многопараметрическую вероятностную экономическую систему. Кроме того, моделирование с помощью имитационных подходов применяется для систем больших размерностей и с большими внутренними связями.
Основные этапы моделирования:
1) анализ моделируемой систем, сбор необходимой информации, выделение проблемной области исследования и постановка задач на исследование;
2) синтезирование (формирование, получение) необходимой математической модели области допустимых упрощений (ограничений), выбор критериев оценки эффективности и точности моделирования;
3) разработка имитационной модели, алгоритма ее реализации, внутреннее и внешнее математическое обеспечение;
4) оценка адекватности имитационной модели и контроль результатов экстремумов с последующей валидацией модели;
5) анализ результатов моделирования с целью достижения заданной точности моделирования.
Похожие работы
... отрезка времени. Как правило, это задача, решение которой влечет за собой постановки близких или аналогичных задач. Глава 2. Экономико-математическое моделирования процессов принятия управленческих решений. В классификации решений по времени действия выражается принцип их цикличности, определенная хронологическая последовательность, временные рамки которой неизбежно должны учитываться в процессе ...
... производственной функции, моделей поведения фирмы, моделей общего экономического равновесия, прежде всего модели Л. Вальраса и ее модификаций. Глава 2. История развития экономико-математического моделирования в США Для характеристики математического направления в экономике за последние 80 – 90 лет приведу лишь некоторые результаты, сыгравшие заметную роль в его развитии. Как в теоретическом, ...
... вопросы должны быть получены в ходе маркетинговых и проектно-изыскательских работ на фазе проектирования спортивных сооружений. И уже на этой стадии в процесс активно включаются экономико-математические методы, задействуется существующий аппарат математического моделирования и прогнозирования. Данные методы и расчеты совершенно необходимы для определения: сроков окупаемости отдельных предприятии ...
... <= 2,10 В разделе 1 проекта требуется: 1. Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала. Нужно формулировать экономико-математическую модель общей задачи линейного программирования (ОЗЛП); 2. С помощью полученных в результате реализации модели отчетов сделать рекомендации филиалу фирмы по расширению программы ...
0 комментариев