Навигация
Модель управления запасами при случайном спросе
6.5. Модель управления запасами при случайном спросе.
В данном случае интенсивность расходования ресурсов b - величина случайная со своим законом распределения, то есть известно P(b), F(b) , тогда в данной ситуации возможны случаи:
1) ![]() q - b > 0
q - b > 0
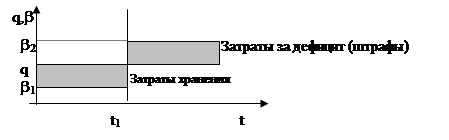
2) ![]()
3) h – затраты на хранение единицы продукции в единицу времени;
4) k – затраты на размещение (оформление) ресурсов, сырья.
Так как b - величина случайная, то ( q - b ) и (b - q) будут величины случайные, поэтому оптимизация и функция цели будут находится как для случайных величин.
Функция цели будет представлять собой математическое ожидание от суммы слагаемых. Одно из них представляет собой математическое ожидание затрат на размещение заказа; другое математическое ожидание затрат на хранение ресурсов.
![]()
Известно, что оптимальное размещение запасов можно найти из системы неравенств:
![]()
Методом линейной интерполяции определяется q*.
6.6. ЭММ управления запасами с ограничениями на складские помещения.
Данная модель многопродуктовая с n-видами сырья.
Введем обозначения для данной модели:
qi– размер объема заказа на сырье i – вида (![]() );
);
А – максимальный размер складских помещений для сохранения n-видов продукции;
аi – размер площади, необходимой для хранения продукции i – вида;
bi – интенсивность спроса на сырье i – вида;
ki – затраты на размещение заказа на поставку сырья, продукции i – вида;
hi – затраты на сохранение единицы сырья (продукции) i – вида.
Данная модель от вышеизложенной отличается наличием ограничений на складские помещения и выглядит так:
![]()
![]()
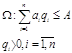
qi / 2 – оптимизация по среднему уровню запасов
Данная ЭММ решается с помощью метода множителей Лагранжа. Полученная функция путем добавления в целевую функцию слагаемого, состоящего из системы ограничений и множителя l, называется Лагранжианом.
![]()
![]() (*)
(*)
Для того, чтобы найти qi* и оптимальное значение l*, необходимо взять частные производные по qi и l Лагранжиана (*).
![]() (1)
(1)
![]() (2)
(2)
из формулы (1) определяем ![]() - оптимальный размер заказа.
- оптимальный размер заказа.
Оптимальный размер заказа при ограничении ai определяется путем последовательного расчета для разных значений qi и l. Методом линейной интерполяции по значениям, представленным в промежуточной таблице, находится коэффициент l и оптимальное значение qi*.
Тема 7. ЭММ систем массового обслуживания.
7.1. Основные понятия и определения.
Система массового обслуживания (СМО) – это совокупность приборов, каналов, станков, линий обслуживания, на которые в случайные или детерминированные моменты времени поступают заявки на обслуживание. Например, коммутаторы телефонных станций, супермаркет, парикмахерские.
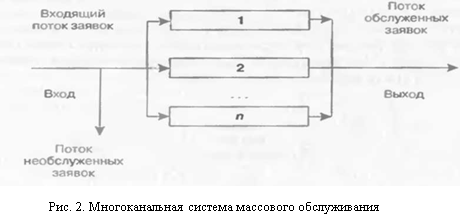
Оптимизация и оценка эффективности СМО состоит в нахождении средних суммарных затрат на обслуживание каждой заявки и нахождение средних суммарных потерь от заявок не обслуженных.
СМО состоит из определенного числа обслуживающих каналов и предназначена для выполнения заявок с разным характером распределения момента времени на обслуживание.
Моделирование СМО предполагает:
1) построение ЭММ, связывающих параметры СМО (число каналов, их производительность и т.п.) с показателями эффективности;
2) оптимизацию данных показателей с целью получения максимальной эффективности.
7.2. Классификация и обозначение СМО.
По ряду признаков СМО делятся на:
1. СМО: - с очередями;
- с отказами заявок (очереди);
2. СМО с очередью: - в порядке очереди;
- в случайном порядке;
- обслуживание с приоритетом (абсолютным или относительным);
3. СМО с многофазным обслуживанием;
4. СМО: - закрытые (замкнутые) – поток заявок генерируется самой системой;
- открытые – характер потока заявок не зависит от состояния СМО;
5. СМО: - одноканальные;
- многоканальные.
Обозначения СМО.
Для сокращения записи и характеристик СМО принята общемировая система записи по формату Кендола.
( a ç b ç c ç) : ( d çe çf )
a –характеризует закон распределения заявок входного потока;
b - характеризует закон распределения интервалов выполнения заявок на обслуживание;
c - характеризует количество каналов обслуживания;
d - характеризует дисциплину очереди;
e - характеризует максимальное количество требований (заявок) на обслуживание (е в очереди + е в обслуживании);
f – максимальный объем источника (генератора) заявок.
Пример.
GI çG ç N
GI - данная позиция характеризует, что момент заявок, поступающих на обслуживание, распределен по случайному закону с функцией распределения F(x) с математическим ожиданием ![]() .
.
F(x) – любой закон распределения;
G - данная позиция характеризует моменты распределения (временные интервалы) обслуживания заявок с любой функцией распределения H(x) и со средним временем обслуживания ![]() .
.
( M1 ç M2 ç N ) : - характеризует, что поток заявок, поступающих на обслуживание как входящий поток, подчиняется закону Пуассона с функцией распределения ![]() ,
,
l - интенсивность потока заявок;
M1 – простейший поток заявок;
N – количество мест по обслуживанию заявок;
M2 – характеризует поток обслуживания и распределения времени обслуживания также по простейшему Пуассоновскому закону с функцией распределения ![]() ,
,
m - характеризует интенсивность потока обслуживания.
Простейший поток обладает тремя свойствами:
1) стационарностью;
2) безпоследействия;
3) ординарностью.
Стационарность – это когда вероятность попадания того или иного числа заявок на интервал времени длиной t зависит от длины этого интервала и не зависит от того, где этот интервал расположен на оси времени.
Поток безпоследействия – когда для любых не перекрывающихся участков времени число заявок, попадающих на один из участков, не зависит от числа заявок, попадающих на другой участок.
Ординарность – это когда вероятность попадания на участок t двух или более заявок пренебрежимо мала по сравнению с вероятностью попадания одной заявки.
Поток, обладающий вышеназванными тремя свойствами, называется простейшим (стационарным, Пуассоновским ) потоком.
Эрланговский поток – “просеянный” простейший поток с коэффициентом k = (2;3;4...), то есть когда обслуживается каждая 2,3,...,k заявка.
El êEm êNM – эрланговский входной поток заявок El и эрланговский закон обслуживания Em.
Похожие работы
... отрезка времени. Как правило, это задача, решение которой влечет за собой постановки близких или аналогичных задач. Глава 2. Экономико-математическое моделирования процессов принятия управленческих решений. В классификации решений по времени действия выражается принцип их цикличности, определенная хронологическая последовательность, временные рамки которой неизбежно должны учитываться в процессе ...
... производственной функции, моделей поведения фирмы, моделей общего экономического равновесия, прежде всего модели Л. Вальраса и ее модификаций. Глава 2. История развития экономико-математического моделирования в США Для характеристики математического направления в экономике за последние 80 – 90 лет приведу лишь некоторые результаты, сыгравшие заметную роль в его развитии. Как в теоретическом, ...
... вопросы должны быть получены в ходе маркетинговых и проектно-изыскательских работ на фазе проектирования спортивных сооружений. И уже на этой стадии в процесс активно включаются экономико-математические методы, задействуется существующий аппарат математического моделирования и прогнозирования. Данные методы и расчеты совершенно необходимы для определения: сроков окупаемости отдельных предприятии ...
... <= 2,10 В разделе 1 проекта требуется: 1. Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала. Нужно формулировать экономико-математическую модель общей задачи линейного программирования (ОЗЛП); 2. С помощью полученных в результате реализации модели отчетов сделать рекомендации филиалу фирмы по расширению программы ...
0 комментариев