Решение линейных уравнений. Решение невырожденых систем
Евклидово пространство. Длина вектора. Угол между векторами
Смешанное произведение трех ненулевых векторов равно нулю тогда и только тогда, когда они компланарны
Характеристическое уравнение линейного оператора. Собственные векторы линейного оператора и их свойства
Угол между прямой и плоскостью. Расстояние от точки до плоскости
Эллипс. Определение. Вывод канонического уравнения
Поверхности 2-го порядка. Параболоиды
Замечательный предел
Навигация
Решение линейных уравнений. Решение невырожденых систем
Шпоры по вышке
27054
знака
0
таблиц
20
изображений
7. Решение линейных уравнений. Решение невырожденых систем.
Метод Гаусса.
Сначала следует привести систему к треугольному (ступенчатому) виду, а затем ступенчато решить.
Формула Крамера.
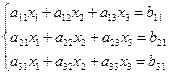
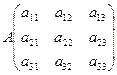
Подсчитать определитель матрицы А.
Затем матрицей B заменить первый столбец матрицы А, подсчитать определитель и разделить его на detA, так мы получим x1. То же самое проделать со 2-ым и 3-им столбцом.
8. Решение произвольных систем. Теорема Кронекера-Капелли.
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.
Найти какой-либо базисный минор порядка r. Взять r уравнений, из которых составлен базисный минор. Неизвестные, коэффициенты которых входят в базисный минор, называются главными и остаются слева, а остальные называются свободными и переносятся в правую часть уравнения. Найдя главные через свободные, получим общее решение системы.
9. Однородные система уравнений. Фундаментальная система решений.
Система однородных уравнений всегда имеет нулевое решение. Если ранг матрицы меньше числа неизвестных, то система имеет бесчисленное множество решений. Для того, чтобы система имела ненулевые решения, необходимо, чтобы ее определитель был равен нулю.
10. Линейные пространства. Линейная зависимость и независимость системы векторов. Размерность и базис линейного пространства.
Рассмотрим непустое множество элементов, которые будем обозначать через x, y, z, … и множество действительных чисел. На этом множестве введем две операции (сложение и умножение). Пусть эти две операции подчиняются аксиомам:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
V; x, y, z, … 
V
Множество V с двумя операциями, удовлетворяющее аксиомам называется линейным пространством.
Элементы линейного пространства называются векторами, обозначаются 
, 
, 
. Существует единственный нулевой элемент, для каждого элемента существует единственный противоположный.
Линейная зависимость и независимость системы векторов. Пусть имеется n векторов.
Составим линейную комбинацию:
, если 
система n векторов – линейно-зависима.
Если среди n векторов какие-то k линейно-зависимы, то вся система векторов является линейно-зависимой.
Если система n векторов линейно-независима, то любая часть из этих векторов будет тоже линейно-независимой.
Размерность и базис линейного пространства. Пусть система n векторов линейно-независима, а любая система n+1 векторов – линейно-зависима, тогда число n называют размерностью пространства. dimV=n
Система этих n линейно-независимых векторов называется базисом линейного пространства. Рассмотрим систему n+1 векторов. 
Такое представление называется разложение по базису, а числа 
называют координатами вектора.
Разложение любого вектора в выбранном базисе - единственно.
11. Матрица перехода от базиса к базису. Преобразование координат вектора при переходе к новому базису.
n – мерное пространство.
Vn – базис, состоящий из n векторов.
В пространстве есть базисы 
Введем матрицу перехода от 
к 
.
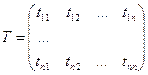
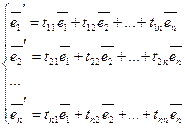
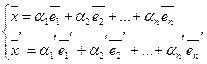
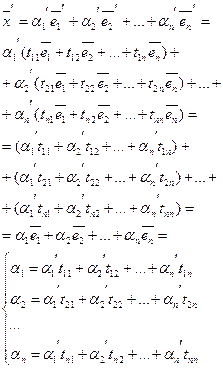
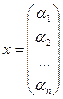
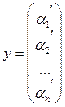
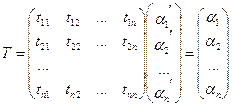
Похожие работы
... для увеличения объема выпуска требуется замена оборудования и постоянные издержки принимают форму переменных. Предельные затраты - дополнительные издержки пр-ва, необходимые для пр-ва дополнительной единицы пр-ции. 17. Экономика пред.. Доход и прибыль пред.. Виды прибыли и ее распределение. Рент. пред.. Виды прибыли. Различают прибыль бухгалтерскую и чистую экономическую прибыль. Как правило, ...
одно малые по модулю.Св-ва сходящихся посл-тей Теорема «Об единственности пределов» Если посл-ть xn сходится, то она имеет единственный предел. Док-во (от противного) {xn} имеет два разл. Предела a и b, аb. Тогда согласно определению пределов любая из окрестностей т. а содержит все эл-ты посл-ти xn за исключением конечного числа и аналогичным св-вом ...
... СКЦ-2М Осреднитель тонн м³ м³ шт шт шт шт шт шт 64,8 6,6 32,4 2 3 3 1 1 2 80,7 6,6 38,8 2 3 4 1 1 2 39 1,1 14 1 4 5 1 1 1 3. ЭКОНОМИЧЕСКИЙ РАСЧЕТ СМЕТА К РАБОЧЕМУ ПРОЕКТУ на строительство эксплуатационной скважины №11 на площади СЕВЕРО-ПРИБРЕЖНАЯ. Цель работ эксплуатация Способ бурения роторный Вид бурения вертикальный ...
... , не то дочь. Не мышонка, не лягушку, А неведому зверушку». Но в сказках добро всегда побеждает зло, а посему интриганки были в конце концов наказаны. Обман в нашей жизни ИСТОРИЯ Бог не может изменить, прошлое, но историки могут. Сэмюэль Батлер Обман, фальсификация и подлоги —.нередкое дело в истории. Человечество накопило их в таком ...
0 комментариев