Решение линейных уравнений. Решение невырожденых систем
Евклидово пространство. Длина вектора. Угол между векторами
Смешанное произведение трех ненулевых векторов равно нулю тогда и только тогда, когда они компланарны
Характеристическое уравнение линейного оператора. Собственные векторы линейного оператора и их свойства
Угол между прямой и плоскостью. Расстояние от точки до плоскости
Эллипс. Определение. Вывод канонического уравнения
Поверхности 2-го порядка. Параболоиды
Замечательный предел
Навигация
Характеристическое уравнение линейного оператора. Собственные векторы линейного оператора и их свойства
Шпоры по вышке
27054
знака
0
таблиц
20
изображений
18. Характеристическое уравнение линейного оператора. Собственные векторы линейного оператора и их свойства.
Если в базисе 
линейный оператор имеет матрицу А, а в базисе (
) оператор имеет матрицу В 
λ – произвольное число ≠0
Е – единичная матрица
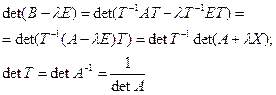
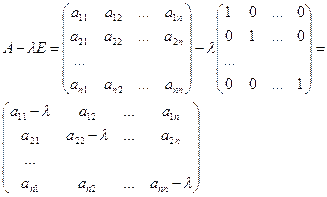Если характеристически многочлен линейного оператора прировнять к 0, получим характеристическое уравнение линейного оператора.
Собственные векторы линейного оператора
Ненулевой вектор 
называется собственным вектором линейного оператора, если 
оператор к , получим этот же , умноженный на некоторое к.
к – собственное число оператора А=
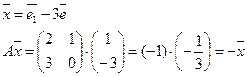
Каждый собственный вектор имеет единственное собственное число.
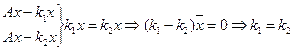
19. Прямая в пространстве. Виды уравнений прямой. Угол между прямыми.
Векторное уравнение прямой.
Положение прямой можно задать по точке и направляющему вектору.
Пусть прямая L задана ее точкой M0(x0;y0;z0) и направляющим вектором S(m;n;p). Возьмем на прямой L точку M(x;y;z). Обозначим радиус-векторы точек M и M0 через r и r0.
Тогда уравнение прямой запишется в виде: 
где t – скалярный множитель (параметр).
Параметрические уравнения прямой.
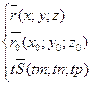
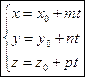
Канонические уравнения прямой.
S(m;n;p) – направляющий вектор прямой L. M0(x0;y0;z0) – точка на прямой. 
соединяет M0 с произвольной точкой М.
Уравнение прямой в пространстве, проходящей через две точки.
M1(x1;y1;z1) M2(x2;y2;z2)
В качестве направляющего вектора можно задать вектор 
Следовательно:
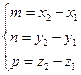, тогда 
Общее уравнение прямой.
Уравнение прямой как линию пересечения двух плоскостей. Рассмотрим:
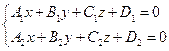
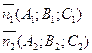
Т.к. прямая перпендикулярна векторам n1 и n2 то направляющий вектор запишется как векторное произведение:
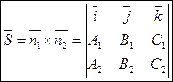
Угол между прямыми.
;
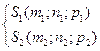
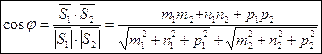
20. Плоскость в пространстве. Виды уравнения плоскостей. Угол между плоскостями.
Уравнение плоскости, проходящей через заданную точку, перпендикулярно данному вектору.
Пусть плоскость задана точкой M0(x0;y0;z0) и вектором 
, перпендикулярной этой плоскости.
Возьмем произвольную точку M(x;y;z) и составим вектор 
. При любом расположении точки М на плоскости Q 
, поэтому 
.
Общее уравнение плоскости.
· Если D=0, то данному уравнению удовлетворяет точка О (0;0;0)
· Если С=0 то вектор 
. Следовательно, плоскость параллельна оси oz, если В=0 – то oy, если А=0 – то ox.
· Если C=D=0, то плоскость проходит через О (0;0;0), параллельно оси oz. Аналогично при A=D=0 и B=D=0.
· Если А=В=0 то уравнение примет вид 
плоскость параллельна плоскости Oxy.
· Если A=B=D=0, то уравнение имеет вид 
. Это уравнение плоскости Oxy.
Уравнение плоскости, проходящей через три точки
К (х1;у1) М (х2;у2) N (x3;y3)
Возьмем на плоскости точку P (x;y;z).
Составим векторы:
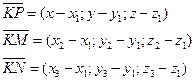
Эти векторы лежат в одной плоскости, следовательно они компланарны:
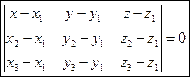
Уравнение плоскости в отрезках.
Пусть плоскость отсекает на осях отрезки, т.е. проходит через точки:
; 
; 
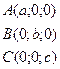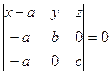Нормальное уравнение плоскости.
Похожие работы
... для увеличения объема выпуска требуется замена оборудования и постоянные издержки принимают форму переменных. Предельные затраты - дополнительные издержки пр-ва, необходимые для пр-ва дополнительной единицы пр-ции. 17. Экономика пред.. Доход и прибыль пред.. Виды прибыли и ее распределение. Рент. пред.. Виды прибыли. Различают прибыль бухгалтерскую и чистую экономическую прибыль. Как правило, ...
одно малые по модулю.Св-ва сходящихся посл-тей Теорема «Об единственности пределов» Если посл-ть xn сходится, то она имеет единственный предел. Док-во (от противного) {xn} имеет два разл. Предела a и b, аb. Тогда согласно определению пределов любая из окрестностей т. а содержит все эл-ты посл-ти xn за исключением конечного числа и аналогичным св-вом ...
... СКЦ-2М Осреднитель тонн м³ м³ шт шт шт шт шт шт 64,8 6,6 32,4 2 3 3 1 1 2 80,7 6,6 38,8 2 3 4 1 1 2 39 1,1 14 1 4 5 1 1 1 3. ЭКОНОМИЧЕСКИЙ РАСЧЕТ СМЕТА К РАБОЧЕМУ ПРОЕКТУ на строительство эксплуатационной скважины №11 на площади СЕВЕРО-ПРИБРЕЖНАЯ. Цель работ эксплуатация Способ бурения роторный Вид бурения вертикальный ...
... , не то дочь. Не мышонка, не лягушку, А неведому зверушку». Но в сказках добро всегда побеждает зло, а посему интриганки были в конце концов наказаны. Обман в нашей жизни ИСТОРИЯ Бог не может изменить, прошлое, но историки могут. Сэмюэль Батлер Обман, фальсификация и подлоги —.нередкое дело в истории. Человечество накопило их в таком ...
0 комментариев