Решение линейных уравнений. Решение невырожденых систем
Евклидово пространство. Длина вектора. Угол между векторами
Смешанное произведение трех ненулевых векторов равно нулю тогда и только тогда, когда они компланарны
Характеристическое уравнение линейного оператора. Собственные векторы линейного оператора и их свойства
Угол между прямой и плоскостью. Расстояние от точки до плоскости
Эллипс. Определение. Вывод канонического уравнения
Поверхности 2-го порядка. Параболоиды
Замечательный предел
Навигация
Поверхности 2-го порядка. Параболоиды
Шпоры по вышке
27054
знака
0
таблиц
20
изображений
28. Поверхности 2-го порядка. Параболоиды.
Эллиптический.
При пересечении поверхности координатами плоскостями Oxz и Oyz получается соответственно параболы 
и 
. Таким образом, поверхность, определяемая уравнением, имеет вид выпуклой, бесконечно расширяющейся чаши.
Гиперболический.
Рассечем поверхность плоскостями z=h. Получим кривую
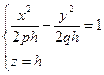
которая при всех h≠0 является гиперболой. При h>0 ее действительные оси параллельны оси Ox, при h<0 – параллельные оси Oy. При h=0 линия пересечения распадается на пару пересекающихся прямых:
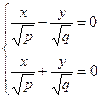
При пересечении поверхности плоскостями, параллельности плоскости Oxz (y=h), будут получаться параболы, ветви которых направлены вверх.
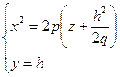
29. Поверхности 2-го порядка. Конусы и цилиндры.
Конус.
Поверхность, образованная прямыми линиями, проходящими через данную точку Р и пересекающими данную плоскую линию L (не проходящую через Р) называется конической поверхностью или конусом. При этом линия L называется направляющей конуса, точка Р – ее вершиной, а прямая, описывающая поверхность, называется образующей.
- уравнение конуса
Цилиндр.
Поверхность, образованная движением прямой L, которая перемещается в пространстве, сохраняя постоянное направление и пересекая каждый раз некоторую кривую К, называется цилиндром. При этом кривая К называется направляющей цилиндра, а прямая L – образующая.
- уравнение цилиндра
30. Исследование кривой второго порядка по ее уравнению без произведения координат.
Уравнение вида Ax2+Cy2+2Dx+2Ey+F=0 всегда определяет либо окружность (при А=С), либо эллипс (при А*С>0), либо гиперболу (при А*С<0), либо параболу (при А*С=0), при этом возможны случаи вырождения: для эллипса (окружности) – в точку или мнимый эллипс (окружность), для гиперболы – в пару пересекающихся прямых, для параболы – в пару параллельных прямых.
Общее уравнение второй степени с двумя неизвестными: Ax2+2Bxy+Cy2+2Dx+2Ey+F=0
Коэффициент В с произведением координат преобразовывает уравнение путем поворота координатных осей.
31. Определение предела числовой функции. Односторонние пределы. Свойства пределов.
Число А называется пределом функции y=f(x) в точке х0, если для любой последовательности допустимых значений аргумента xn, n?N (xn≠x0), сходящейся к х0
(т.е. 
), последовательность соответствующих значений функции f(xn), n?N, сходится к числу А, т.е. 
. Геометрический смысл предела этой функции, что для всех точек х, достаточно близких к точке х0, соответствующие значения функции как угодно мало отличается от числа А.
Односторонние пределы.
Считается, что х стремится к х0 любым способом: оставаясь меньшим, чем х0 (слева от х0), большим, чем х0 (справа от х0), или колеблясь около точки х0.
Число А1 называется пределом функции y=f(x) слева в точке х0, если для любого ε<0 существует число σ=σ(ε)>0 такое, что при х?(x0-σ;x0), выполняется неравенство |f(x)-A1|<ε 
Пределом функции справа называется
Свойства пределов.
1) если предел 
функция равна этому числу плюс б.м.
ε – сколь угодно малое число
|f(x)-a|=α; f(x)=a+ α
2) сумма конечного числа б.м. чисел есть б.м. число
3) предел произведения равен произведению пределов
4) константы можно выносить за знак предела
5) 
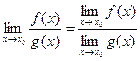
32. Замечательные пределы.
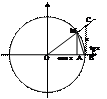
1 замечательный предел.
Возьмем круг радиуса 1, обозначим
радианную меру угла MOB через Х.
Пусть 0 < X < π/2. На рисунке |АМ| = sin x, дуга МВ численно равна центральному углу Х, |BC| = tg x. Тогда
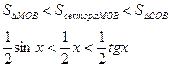
Разделим все на 
и получим:
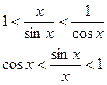
Т.к. 
, то по признаку существования пределов следует 
.
Похожие работы
... для увеличения объема выпуска требуется замена оборудования и постоянные издержки принимают форму переменных. Предельные затраты - дополнительные издержки пр-ва, необходимые для пр-ва дополнительной единицы пр-ции. 17. Экономика пред.. Доход и прибыль пред.. Виды прибыли и ее распределение. Рент. пред.. Виды прибыли. Различают прибыль бухгалтерскую и чистую экономическую прибыль. Как правило, ...
одно малые по модулю.Св-ва сходящихся посл-тей Теорема «Об единственности пределов» Если посл-ть xn сходится, то она имеет единственный предел. Док-во (от противного) {xn} имеет два разл. Предела a и b, аb. Тогда согласно определению пределов любая из окрестностей т. а содержит все эл-ты посл-ти xn за исключением конечного числа и аналогичным св-вом ...
... СКЦ-2М Осреднитель тонн м³ м³ шт шт шт шт шт шт 64,8 6,6 32,4 2 3 3 1 1 2 80,7 6,6 38,8 2 3 4 1 1 2 39 1,1 14 1 4 5 1 1 1 3. ЭКОНОМИЧЕСКИЙ РАСЧЕТ СМЕТА К РАБОЧЕМУ ПРОЕКТУ на строительство эксплуатационной скважины №11 на площади СЕВЕРО-ПРИБРЕЖНАЯ. Цель работ эксплуатация Способ бурения роторный Вид бурения вертикальный ...
... , не то дочь. Не мышонка, не лягушку, А неведому зверушку». Но в сказках добро всегда побеждает зло, а посему интриганки были в конце концов наказаны. Обман в нашей жизни ИСТОРИЯ Бог не может изменить, прошлое, но историки могут. Сэмюэль Батлер Обман, фальсификация и подлоги —.нередкое дело в истории. Человечество накопило их в таком ...
0 комментариев