Навигация
Общее понятие группировок
2.1. Общее понятие группировок.
Группировки являются таки методом исследований социально-экономических явлений, при котором статистическая совокупность делится на однородные группы, которые раскрывают состояние и развитие всей совокупности.
Группировка является важнейшим этапом статистического исследования, соединяющим сбор первичной информации об объеме исследования и анализ этой информации на основе обобщающих статистических показателей.
Методы группировок разнообразны. Это разнообразие обусловлено с одной стороны огромным множеством признаков, подвергаемых статистическому исследованию, а с другой стороны разнообразными задачами, которые решаются на основе группировок.
2.2. Важнейшая проблема возникающая при группировке.
Важнейшая проблема при построении группировки, является выбор группированного признака или основание группировки.
Группировочный признак - варьирующий признак по которому производится объединение единиц совокупности в группы.
По характеру варьирования, признаки разделяются, как известно, на: атрибутивные и количественные. Это деление определяет особенности решения второй проблемы группировок, а именно - определение числа выделяемых групп. При выборе в качестве группировочных некоторых атрибутивных признаков, может быть выделено только строго определенное количество групп. В частности при группировке населения по полу может быть выделено ...
При группировке предприятий по прибыли может быть выделено 3 группы.
Для многих атрибутивных признаков разрабатываются устойчивые группировки, называемые классификацией. Например: классификация отраслей экономики, классификация занятий населения и др.
При группировке по количественному признаку, вопрос о количестве границы групп следует решать исходя из сущности изучаемого социально-экономического явления. При этом следует принимать во внимание такой показатель, как размах вариаций. Чем больше размах варьирования, тем больше образуется групп и наоборот. Необходимо также принимать во внимание численность единиц совокупности по которой строится группировка. При небольшом объеме совокупности, нецелесообразно образовывать большое число групп, т.к. в этом случае в группах не будет достаточного числа единиц для выявления статистических закономерностей.
Существенным вопросом при группировке по количественному признаку является определение интервалов. Показатели числа групп и величины интервалов находятся в обратной зависимости. Чем больше величина интервалов - тем меньше требуется групп и наоборот.
Интервалом называется разность между его верхней и нижней границей.
По величине группировочного признака интервалы подразделяются на равные и неравные. Равные интервалы применяются в тех случаях, когда изменение группировочного признака внутри совокупности происходит равномерно. Расчет величины равного интервала производится по формуле:
k - число групп
Xmax, Xmin - соответственно наибольшее и наименьшее значение признака к качеству групп.
Если распределение группировочного признака внутри совокупности неравномерное, то используются неравные интервалы. Неравные интервалы могут быть прогрессивно возрастающими и прогрессивно убывающими. часто при группировке применяются так называемые специализированные интервалы, т.е. такие, которые определяются исходя из цели исследования и сущности явления. Например: при группировке имеющей целью охарактеризовать трудоспособное население страны используются пятилетние интервалы возраста людей.
Третьей проблемой построения группировок является обозначение границ интервалов. При выделении интервалов по дискретным количественным признакам следует обозначать их границы т.о., чтобы нижняя граница последующего интервала отличалась от верхней границы предыдущего на единицу.
При группировке по непрерывному количественному признаку границы обозначаются так, чтобы группы были четко отделены одна от другой. Это достигается добавлением числовым границам интервалов указаниям о том, куда следует относить единицу обладающей группировочным признаком в размерах точно совпадающих с границами интервалов. Обычно дополнительные разъяснения к числовым границам интервалов образуемым по непрерывным количественным принципам выражаются словами: «более», «менее», «свыше» и т.д.
2.3. Виды группировок.
В зависимости от задач, решаемых с помощью группировок выделяют следующие их виды:
- типологические
- структурные
- аналитические
Главная задача типологической состоит в классификации социально-экономических явлений путем выделения однородных к качественным отношениям групп.
Качественная однородность при этом понимается в том смысле, что в отношении изучаемого свойства все единицы совокупности подчиняются одному закону развития. Например: группировка предприятиям отраслей экономики.
Абсолютные и относительные величины.
Абсолютной величиной называется показатель, выражающий размеры социально-экономического явления.
Относительной величиной в статистике называется показатель, выражающий количественное соотношение между явлениями. Он получается в результате деления одной абсолютной величины на другую абсолютную величину. Величина с которой мы производим сравнения называется основанием или базой сравнения.
Абсолютные величины - всегда величины именованные.
Относительные величины выражаются в коэффициентах, процентах, промили и т.д.
Относительная величина показывает, во сколько раз, или на сколько процентов сравниваемая величина больше или меньше базы сравнения.
В статистике различают 8 видов относительных величин:
1. Сущность и значение средних величин.
Средние величины являются одними из наиболее распространенных обобщающих статистических показателей. Они имеют своей целью одним числом охарактеризовать статистическую совокупность состоящую из меньшинства единиц. Средние величины тесно связаны с законом больших чисел. Сущность этой зависимости заключается в том, что при большом числе наблюдений случайные отклонения от общей статистики взаимопогашаются и в среднем более отчетливо проявляется статистическая закономерность.
С помощью метода средних решаются следующие основные задачи:
1. Характеристика уровня развития явлений.
2. Сравнение двух или нескольких уровней.
3. Изучение взаимосвязей социально-экономических явлений.
Анализ размещения социально-экономических явлений в пространстве.
Для решения этих задач статистическая методология разработала различные виды средних.
2. Среднее арифметическое.
Для выяснения методики расчета средней арифметической используем следующие обозначения:
X - арифметический признак
X (X1, X2, ... X3) - варианты определенного признака
n - число единиц совокупности
- средняя величина признака
В зависимости от исходных данных средняя арифметическая может быть рассчитана двумя способами:
1. Если данные статистического наблюдения на сгруппированы, или сгруппированные варианты имеют одинаковые частоты, то рассчитывается средняя арифметическая простая:
2. Если частоты сгруппированы в данных разные, то рассчитывается среднее арифметическое взвешанное:
- численность (частоты) вариантов
- сумма частот
Среднее арифметическое рассчитывается по разному в дискретных и интервальных вариационных рядах.
В дискретных рядах варианты признака умножаются на частоты, эти произведения суммируются и полученная сумма произведений делится на сумму частот.
Рассмотрим пример вычисления средней арифметической в дискретном ряду:
| Заработная плата, руб. Xi | Число сотрудников, чел. fi | Произведение вариант на веса (частоты) Xi*fi |
| 1200 | 1 | 1200 |
| 1300 | 2 | 2600 |
| 1400 | 2 | 2800 |
| 1500 | 5 | 7500 |
| 1600 | 3 | 4800 |
| 1650 | 2 | 3300 |
| 1700 | 1 | 1700 |
| 1750 | 1 | 1750 |
| 1800 | 1 | 1800 |
| 1950 | 1 | 1950 |
| 2000 | 1 | 2000 |
| Итого: | 20 | 31400 |
В интервальных рядах значение признака задано, как известно, в виде интервалов, поэтому, прежде чем рассчитывать среднюю арифметическую, нужно перейти от интервального ряда к дискретному.
В качестве вариантов Xi используется середина соответствующих интервалов. Они определяются как полусумма нижней и верхней границ.
Если у интервала отсутствует нижняя граница, то его середина определяется как разность между верхней границей и половиной величины следующих интервалов. При отсутствии верхних границ, середина интервала определяется как сумма нижней границы и половины величины предыдущего интервала. После перехода к дискретному ряду дальнейшие вычисления происходят по методике рассмотренной выше.
Если веса fi заданы не в абсолютных показателях, а в относительных, то формула расчета средней арифметической будет следующей:
pi - относительные величины структуры, показывающие, какой процент составляют частоты вариантов в сумме всех частот.
Если относительные величины структуры заданы не в процентах, а в долях, то среднее арифметическое будет рассчитываться по формуле:
Похожие работы
... экономико-рыночных отношений в нашей стране ставит перед школой новые задачи. Умение анализировать, сравнивать различные ситуации необходимо на сегодняшний день каждому современному человеку. Элективный курс «Общая теория статистики» с помощью математического аппарата даст начальные понятия о статистике, которые необходимы при решении управленческих задач. Курс рассчитан для учащихся 11 класса ...
... ; q1, q2 - объем отчетного, базисного периодов соответственно) для величины (цены) по каждому виду товара для величины q (объема) по каждому виду товаров: Найдем общие индексы по формулам: представляет собой среднее значение индивидуальных индексов (цены, объема), где j – номер товара. Общий индекс товарооборота равен: Найдем абсолютное ...

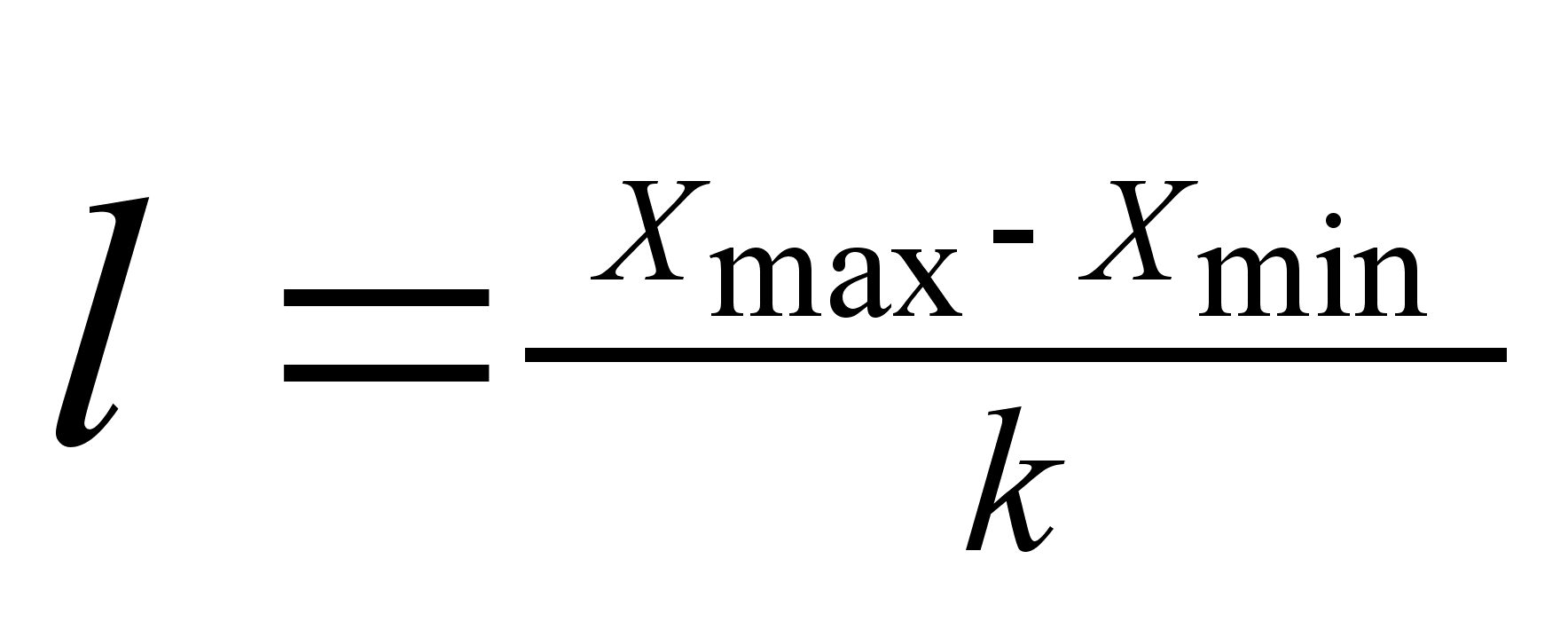
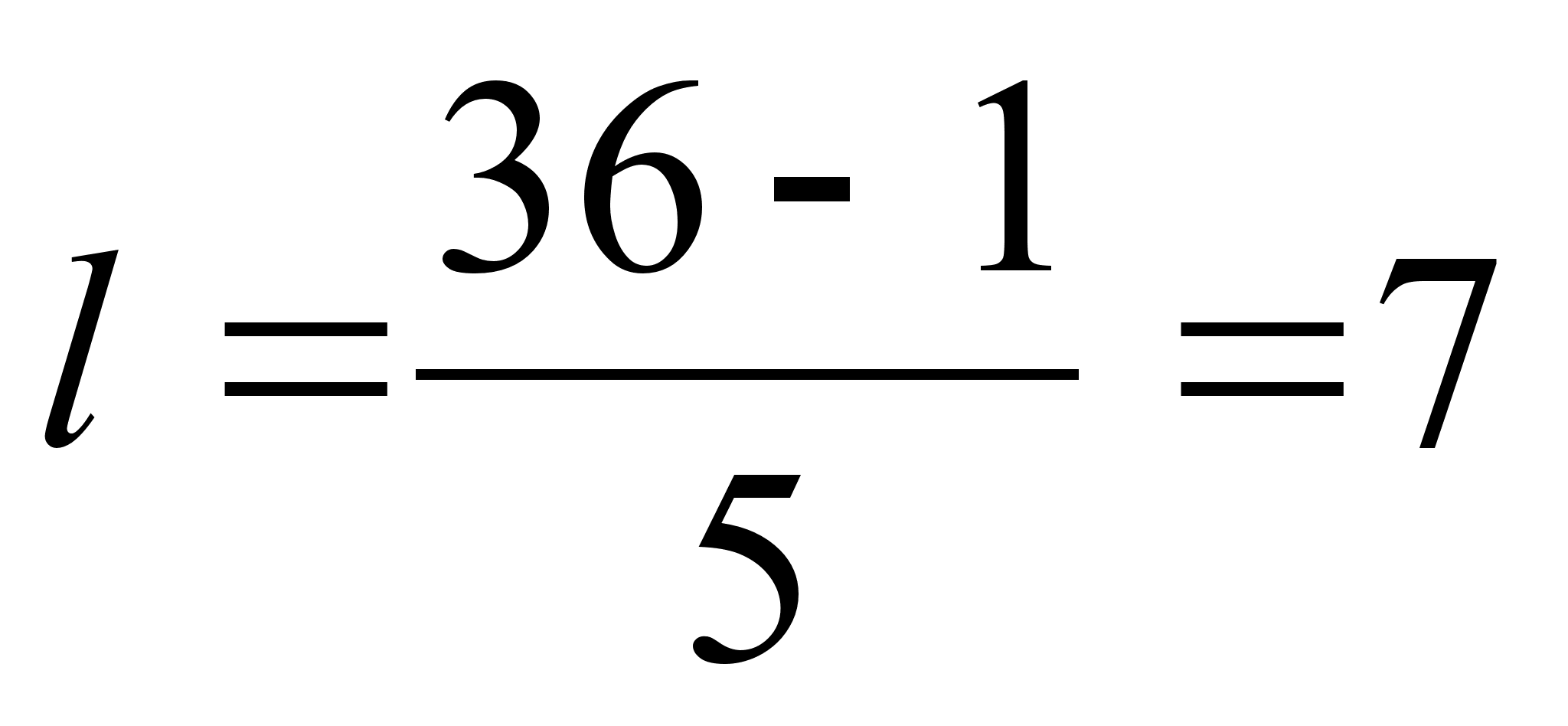
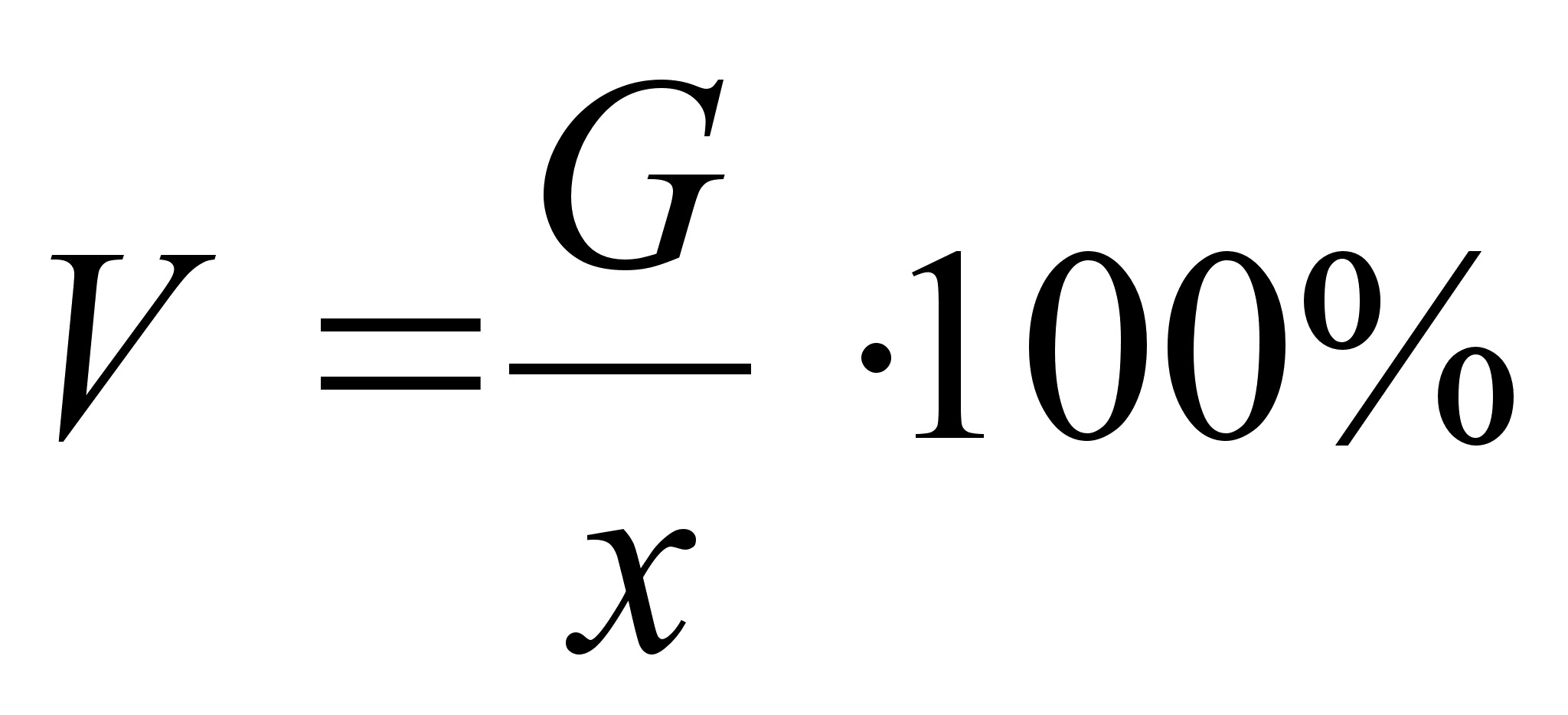
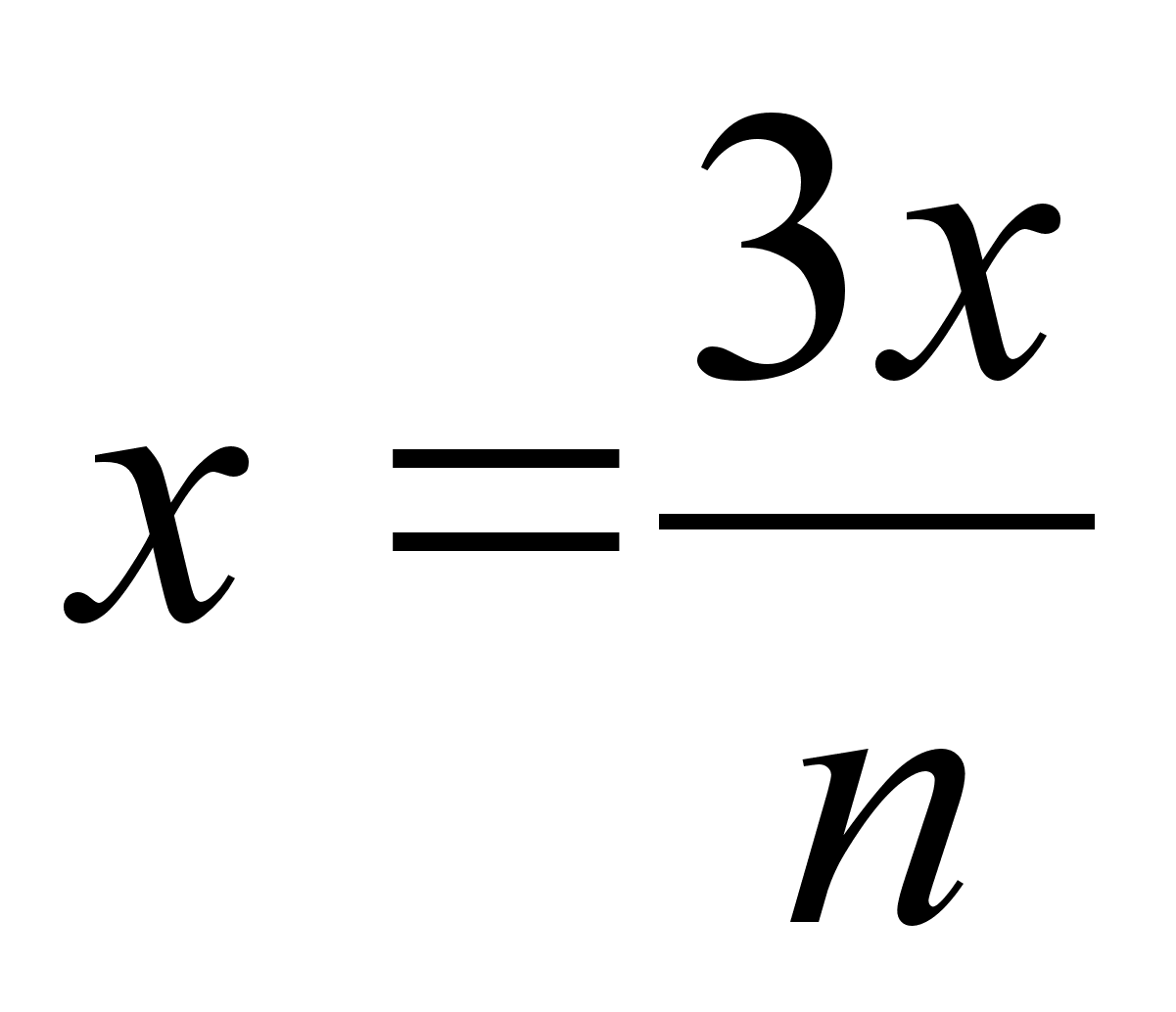
0 комментариев