Навигация
Средняя гармоническая
3. Средняя гармоническая.
Средняя гармоническая является первообразной формой средней арифметической. Она рассчитывается в тех случаях, когда веса fi не заданы непосредственно, а входят как сомножитель в один из имеющихся показателей. Также как и арифметическая, средняя гармоническая может быть простой и взвешанной.
Средняя гармоническая невзвешанная:
Средняя гармоническая смешанная:
Wi - произведение вариантов на частоты
При расчете средних величин необходимо помнить о том, что всякие промежуточные вычисления должны приводить как в числителе, так и в знаменателе и имеющим экономический смысл показателям.
4. Структурное среднее.
Структурное среднее характеризует состав статистической совокупности по одному из варьирующих признаков. К этим средним относятся мода и медиана.
Мода - такое значение варьирующего признака, которое в данном ряду распределения имеет наибольшую частоту.
В дискретных рядах распределений мода определяется визуально. Сначала определяется наибольшая частота, а по ней модальное значение признака. В интервальных рядах для вычисления моды используется следующая формула:
Xmo - нижняя граница модальности (интервал ряда с наибольшей частотой)
Mo - величина интервала
fMo - частота модального интервала
fMo-1 - частота интервала предшествующего модальному
fMo+1 - частота интервала следующего за модальным
Медианой называется такое значение варьирующего признака, которое делит ряд распределения на две равные части по объему частот. Медиана рассчитывается по разному в дискретных и интервальных рядах.
1. Если ряд распределения дискретный и состоит из четного числа членов, то медиана определяется как средняя величина из двух серединных значений рангированного ряда признаков.
2. Если в дискретном ряду распределения нечетное число уровней, то медианой будет серединное значение рангированного ряда признаков.
В интервальных рядах медиана определяется по формуле:
- нижняя граница медианного интервала (интервала для которого накопленная частота впервые превысит полусумму частот)
Me - величина интервала
- сумма частот ряда
- сумма накопленных частот предшествующих медианному интервалу
- частота медианного интервала
1. Общее понятие о вариации.
Вариацией называется различие значений признака у отдельных единиц совокупности.
Вариация возникает в силу того, что отдельные значения признака формируются по влияние большого числа взаимосвязанных факторов. Эти факторы часто действуют в противоположных направлениях и их совместное действие формирует значение признаков у конкретной единицы совокупности. Необходимость изучения вариаций связана с тем, что средняя величина, обобщающая данные статистического наблюдения, на показывает как колеблется вокруг нее индивидуальное значение признака. Вариации присущи явлениям природы и общества. При этом революция в обществе происходит быстрее, чем аналогичные изменения в природе. Объективно существуют также вариации в пространстве и во времени.
Вариации в пространстве показывают различие статистических показателей относящихся к различным административно-территориальным единицам.
Вариации во времени показывают различие показателей в зависимости от периода или момента времени к которым они относятся.
2. Меры вариаций.
К примерам вариаций относятся следующие показатели:
1. размах вариаций
2. среднее линейное отклонение
3. среднее квадратическое отклонение
4. дисперсия
5. коэффициент
1. Размах вариаций является ее простейшим показателем. Он определяется как разность между максимальным и минимальным значение признака. Недостаток этого показателя заключается в том, что он зависит только от двух крайних значений признака (min, max) и не характеризует колеблимость внутри совокупности. R=Xmax-Xmin.
2. Среднее линейное отклонение является средней величиной абсолютных значений отклонений от средней арифметической. Оно определяется по формуле:
- простая
Отклонения берутся по модулю, т.к. в противном случае, из-за математических свойств средней величины, они всегда были бы равны нулю.
4. Дисперсия (средний квадрат отклонений) имеет наибольшее применение в статистике как показатель меры колеблимости.
Дисперсия определяется по формулам:
пример: стр. 36
Дисперсия является именованным показателем. Она измеряется в единицах соответствующих квадрату единиц измерения изучаемого признака. В данном случае она показывает, что средний размер отклонения прибыли по 50 предприятиям от средней прибыли составляет 1,48.
Дисперсия может быть также определена по формуле:
;
3. Среднее квадратическое отклонение определяется как корень из дисперсии.
По исходным данным приведенным выше, среднее квадратическое отклонение равно:
5. Коэффициент вариаций определяется как отношение среднего квадратического отклонения к средней величине признака, выраженное в процентах:
Он характеризует количественную однородность статистической совокупности. Если данный коэффициент < 50%, то это говорит об однородности статистической совокупности. Если же совокупность не однородна, то любые статистические исследования можно проводить только внутри выделенных однородных групп.
Похожие работы
... экономико-рыночных отношений в нашей стране ставит перед школой новые задачи. Умение анализировать, сравнивать различные ситуации необходимо на сегодняшний день каждому современному человеку. Элективный курс «Общая теория статистики» с помощью математического аппарата даст начальные понятия о статистике, которые необходимы при решении управленческих задач. Курс рассчитан для учащихся 11 класса ...
... ; q1, q2 - объем отчетного, базисного периодов соответственно) для величины (цены) по каждому виду товара для величины q (объема) по каждому виду товаров: Найдем общие индексы по формулам: представляет собой среднее значение индивидуальных индексов (цены, объема), где j – номер товара. Общий индекс товарооборота равен: Найдем абсолютное ...

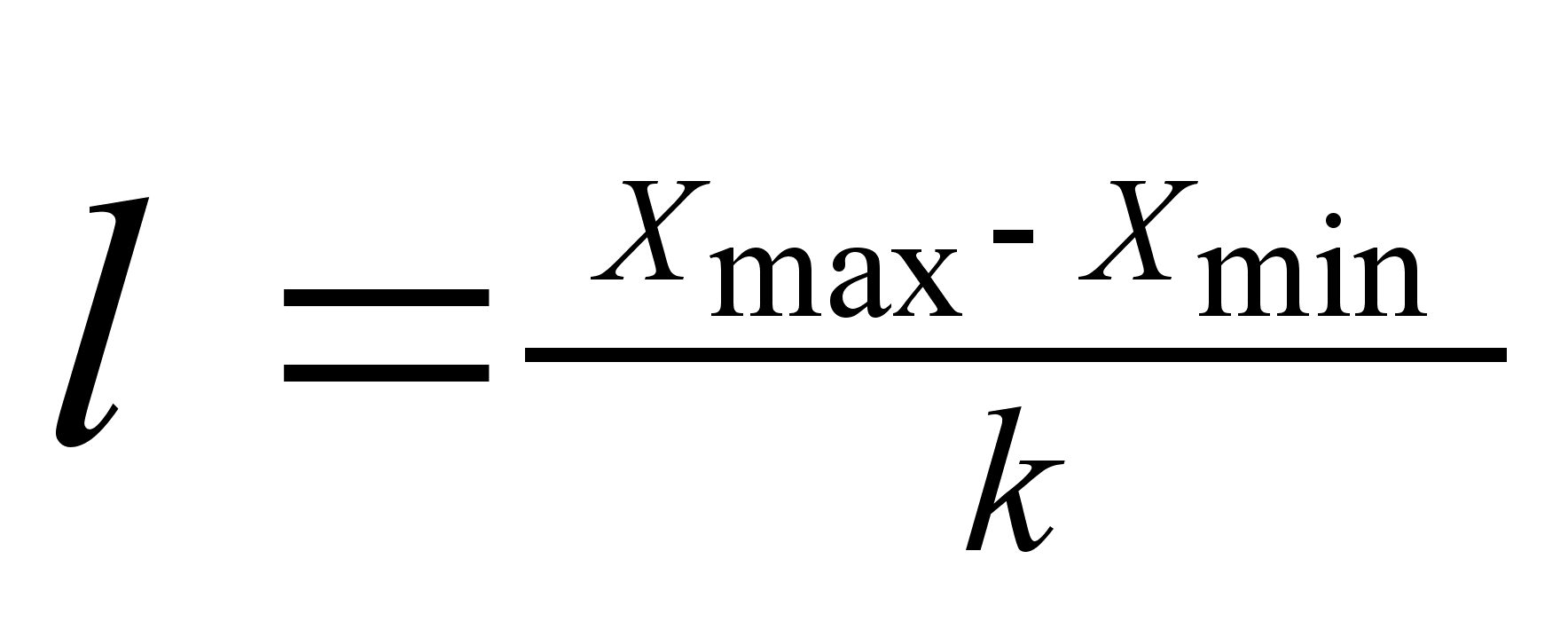
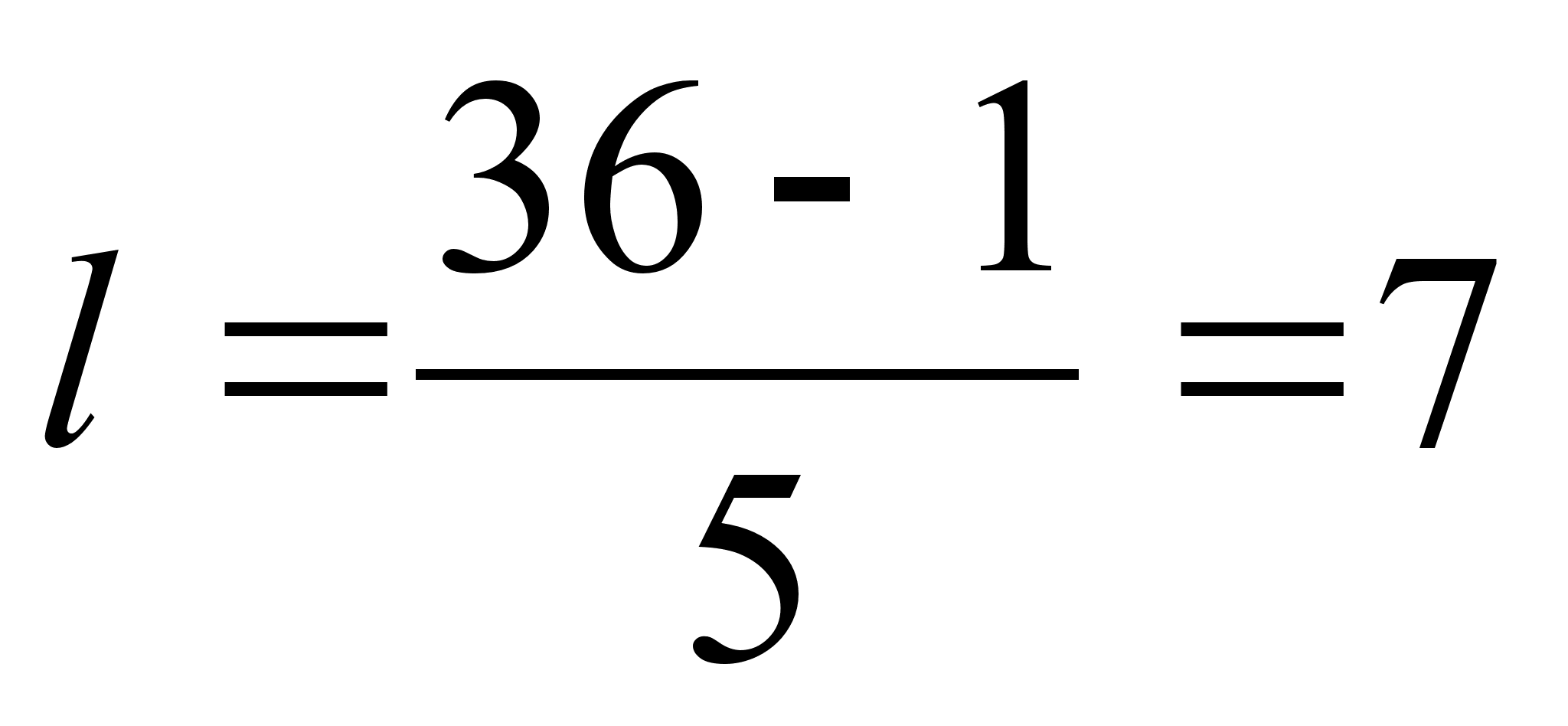
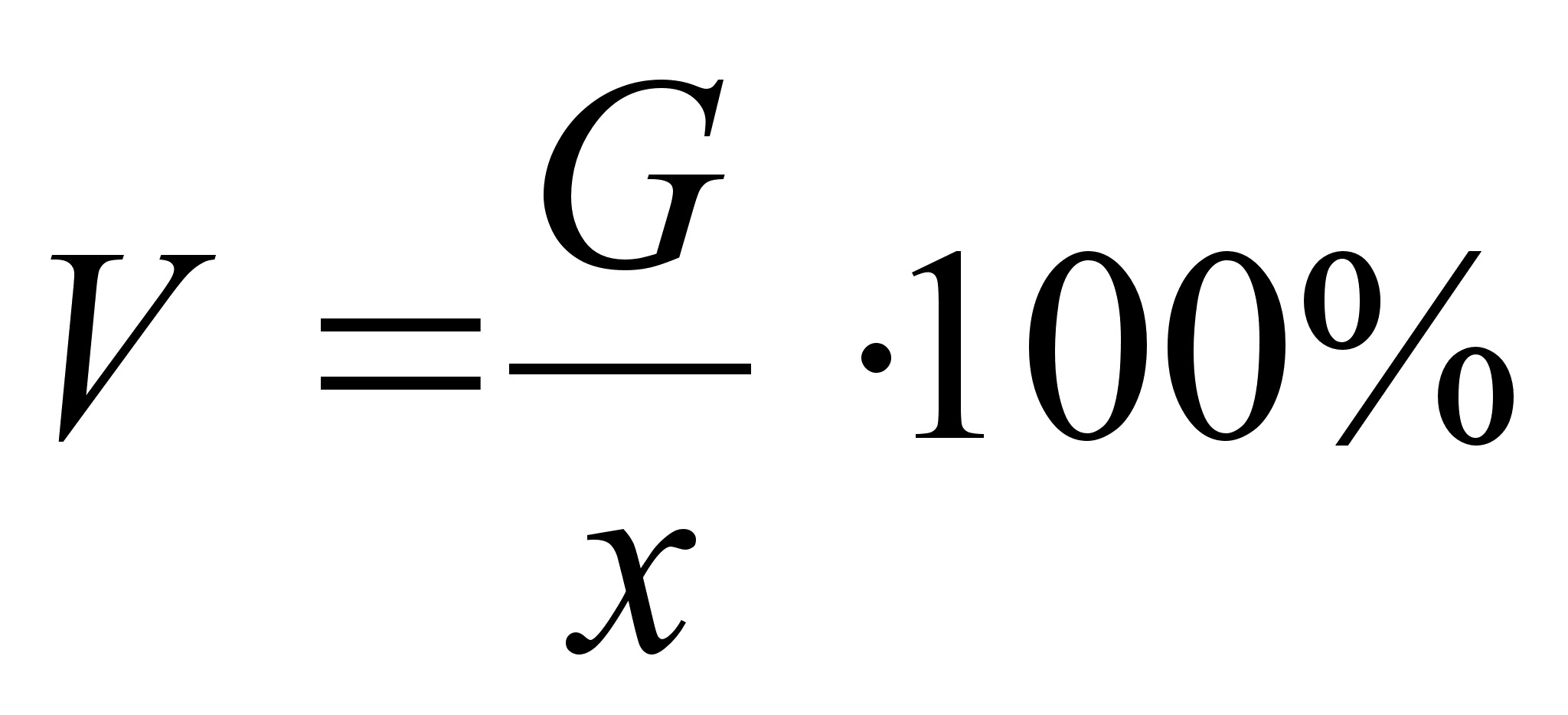
0 комментариев