Навигация
Изучение зависимости между количественными признаками
3. Изучение зависимости между количественными признаками.
Для исследования взаимосвязи качественных альтернативных признаков, принимающих только 2 взаимоисключающих значения, используется коэффициент ассоциации и контингенции. При расчете этих коэффициентов составляется т.н. таблица 4-х камней, а сами коэффициенты рассчитываются по формуле:
| Группы по признаку Y | Группы по признаку X | + | - | Итого: |
| + | a | b | a+b | |
| - | c | d | c+d | |
| Итого: | a+c | c+d | a+b+c+d | |
Если коэффициент ассоциации 0,5, а коэффициент контингенции 0,3, то можно сделать вывод о наличии существенной зависимости между изучаемыми признаками.
Если признаки имеют 3 или более градаций, то для изучения взаимосвязей используются коэффициенты Пирсена и Чупрова. Они рассчитываются по формулам:
С - коэффициент Пирсена
К - коэффициент Чупрова
- показатель взаимной сопряженности
K - число значений (групп) первого признака
K1 - число значений (групп) второго признака
fij - частоты соответствующих клеток таблицы
mi - столбцы таблицы
nj - строки
Для расчета коэффициентов Пирсена и Чупрова составляется вспомогательная таблица:
| Группа признака Y | Группа признака X | 1 | 2 | ... | i | Итого: |
| 1 | f11 | f12 | ... | f1i | n1 | |
| 2 | f21 | f22 | ... | f2i | n2 | |
| ... | ... | ... | ... | ... | ... | |
| j | fji | fj2 | ... | fji | nj | |
| Итого: | m1 | m2 | ... | mi | minj | |
При ранжировании качественных признаков с целью изучения их взаимосвязи используется коэффициент корреляции Кэндалла.
n - число наблюдений
S - сумма разностей между числом последовательностей и числом инвервий по второму признаку.
S=P+Q
P - сумма значений рангов, следующих за данными и превышающих его величину
Q - сумма значений рангов, следующих за данными и меньших его величины (учитывается со знаком «-»).
При наличии связанных рангов формула коэффициента Кендалла будет следующей:
Vx и Vy определяются отдельно для рангов X и Y по формуле:
5. Методы выявления основной тенденции рядов динамики.
Уровни ряда динамики формируются под вниманием 3-х групп факторов:
1. Факторов определяющих основное направление, т.е. тенденцию развития изучаемого явления.
2. Факторов действующих периодически, т.е. направленных колебаний по неделям месяца, месяцам года и т.д.
3. Факторов действующих в разных, иногда в противоположных направлениях и не оказывающих существенного влияния на уровень данного ряда динамики.
Основной задачей статистического изучения данамики является выявление тенденции.
Основными методами выявления тенденции рядов динамики являются:
- метод укрупнения интервалов
- метод скользящей средней
- метод аналитического выравнивания
1. Сущность метода укрупнения интервалов заключается в следующем:
Исходный ряд динамики преобразуется и заменяется другими состоящими из других уровней, относящихся к укрупненным периодам или моментам времени.
Например: ряд динамики прибыли малого предприятия за 1997 год по кварталам того же года. При этом уровни ряда за укрупненные периоды или моменты времени могут представлять собой либо суммарные, либо средние показатели. Однако в любом случае рассчитанные таким образом уровни ряда более отчетливо выявляют тенденции, поскольку сезонные и случайные колебания при суммировании или определении средних взаимопогашаются и уравновешиваются.
2. Метод скользящей средней, как и предыдущий предполагает преобразование исходного ряда динамики. Для выявления тенденции формируются интервал, состоящий из одинакового числа уровней. При этом каждый последующий интервал получается путем смещения на 1 уровень от начального. По образованным таким образом интервалам определяются в начале сумма, а затем средние. Технически удобнее определять скользящие средние для нечетного интервала. В этом случае рассчитанная средняя величина будет относиться к конкретному уровню ряда динамики, т.е. к середине интервала скольжения.
При определении скользящей средней по четному интервалу, расчетное значение средней величины относится к промежутку между двумя уровнями, и таким образом теряют экономический смысл. Это делает необходимыми дополнительные расчеты связанные с центрированием по формуле арифметической простой из двух соседних не центрированных средних.
ШВАЧКИН МАКСИМ ДЭ-103
1. Предмет статистики.
2. Особенности статистической методологии. Метод статистики.
3. Теоретические основы статистики.
4. Основные категории статистической науки.
5. Отрасли статистической науки.
6. Общая теория статистики как отрасль статистической науки.
7. Основные задачи и принципы организации государственной статистики в России.
8. Понятие о статистическом наблюдении, этапы его проведения.
9. Основные формы и виды статистического наблюдения.
10. Программно-методологические вопросы статистического наблюдения.
11. Организационные вопросы статистического наблюдения.
12. Виды несплошного статистического наблюдения.
13. Точность статистического наблюдения. Контроль материалов статистического наблюдения.
14. Сущность и значение статистических группировок, их виды.
15. Основные проблемы возникающие при построении группировок.
16. Типологические группировки.
17. Структурные группировки.
18. Аналитические группировки.
19. Построение группировок по количественному признаку.
20. Вторичная группировка.
21. Ряды распределения, их графическое изображение.
22. Абсолютные и относительные величины.
23. Единицы измерения абсолютных и относительных показателей.
24. Виды статистических относительных величин.
25. Взаимосвязи относительных величин.
26. Статистические таблицы, их виды.
27. Основные правила построения статистических таблиц.
28. Разработка сказуемого статистической таблицы.
29. Таблицы и матрицы.
30. Таблицы сопряженности.
31. Чтение и анализ статистической таблицы.
32. Статистический график, его элементы и правила построения.
33. Классификация видов графиков.
34. Графическое изображение структуры социально-экономических явлений.
35. Графическое изображение динамики социально-экономических явлений.
36. Средняя величина как категория статистики.
37. Виды средних величин.
38. Средняя арифметическая и ее свойства.
39. Виды структурных средних.
40. Мода и медиана, их определение в вариационных рядах.
41. Понятие вариации и ее значение.
42. Сущность и значение показателей вариации.
43. Абсолютные показатели вариации.
44. Дисперсия и ее свойства.
45. Внутригрупповая и межгрупповая вариация.
46. Правило сложения дисперсий.
47. Взаимосвязи общественных явлений, их виды, формы.
48. Определение степени тесноты корреляционной зависимости.
49. Коэффициенты знаков Фехнера и ранговой корреляции Спирмена.
50. Анализ взаимосвязей качественных признаков.
51. Методы статистического изучения взаимосвязи социальных явлений.
52. Непараметрические показатели тесноты взаимосвязи.
53. Показатели взаимной сопряженности.
54. Понятие ранга динамики. Виды динамических рядов.
55. Сопоставимость уровней и смыкание рядов динамики.
56. Аналитические показатели ряда динамики.
57. Средние аналитические показатели ряда динамики.
58. Средние показатели рядов динамики и методика их определения.
59. Интерпретация основных аналитических показателей ряда динамики.
60. Компоненты ряда динамики.
61. Методы выявления тенденции рядов динамики.
62. Определение основной тенденции динамики на основе укрупнения интервалов и скользящей средней.
63. Определение основной тенденции методом аналитического выравнивания.
64. Роль индексного метода в статистических исследованиях.
65. Агрегатные индексы, их взаимосвязи.
66. Индивидуальные и сводные агрегатные индексы.
67. Важнейшие экономические индексы и их взаимосвязь.
68. Индексы производительности труда.
69. Индексы в среднеарифметической и среднегармонической форме.
70. Правила построения индексов объемных и качественных показателей.
71. Цепные и базисные индексы с переменными и постоянными весами.
72. Индексный анализ структурных сдвигов.
73. Статистическое изучение структуры и структурных сдвигов.
74. Индексы пространственно-территориального сопоставлен
Похожие работы
... экономико-рыночных отношений в нашей стране ставит перед школой новые задачи. Умение анализировать, сравнивать различные ситуации необходимо на сегодняшний день каждому современному человеку. Элективный курс «Общая теория статистики» с помощью математического аппарата даст начальные понятия о статистике, которые необходимы при решении управленческих задач. Курс рассчитан для учащихся 11 класса ...
... ; q1, q2 - объем отчетного, базисного периодов соответственно) для величины (цены) по каждому виду товара для величины q (объема) по каждому виду товаров: Найдем общие индексы по формулам: представляет собой среднее значение индивидуальных индексов (цены, объема), где j – номер товара. Общий индекс товарооборота равен: Найдем абсолютное ...

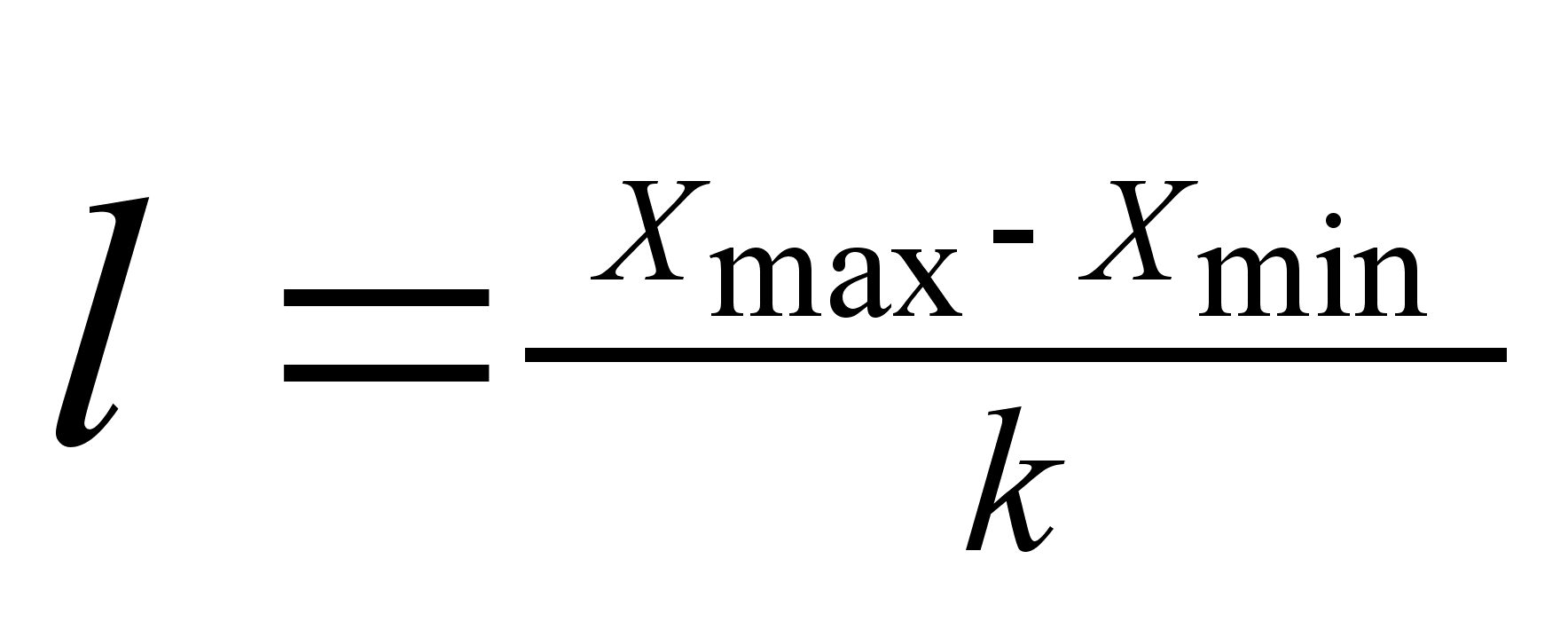
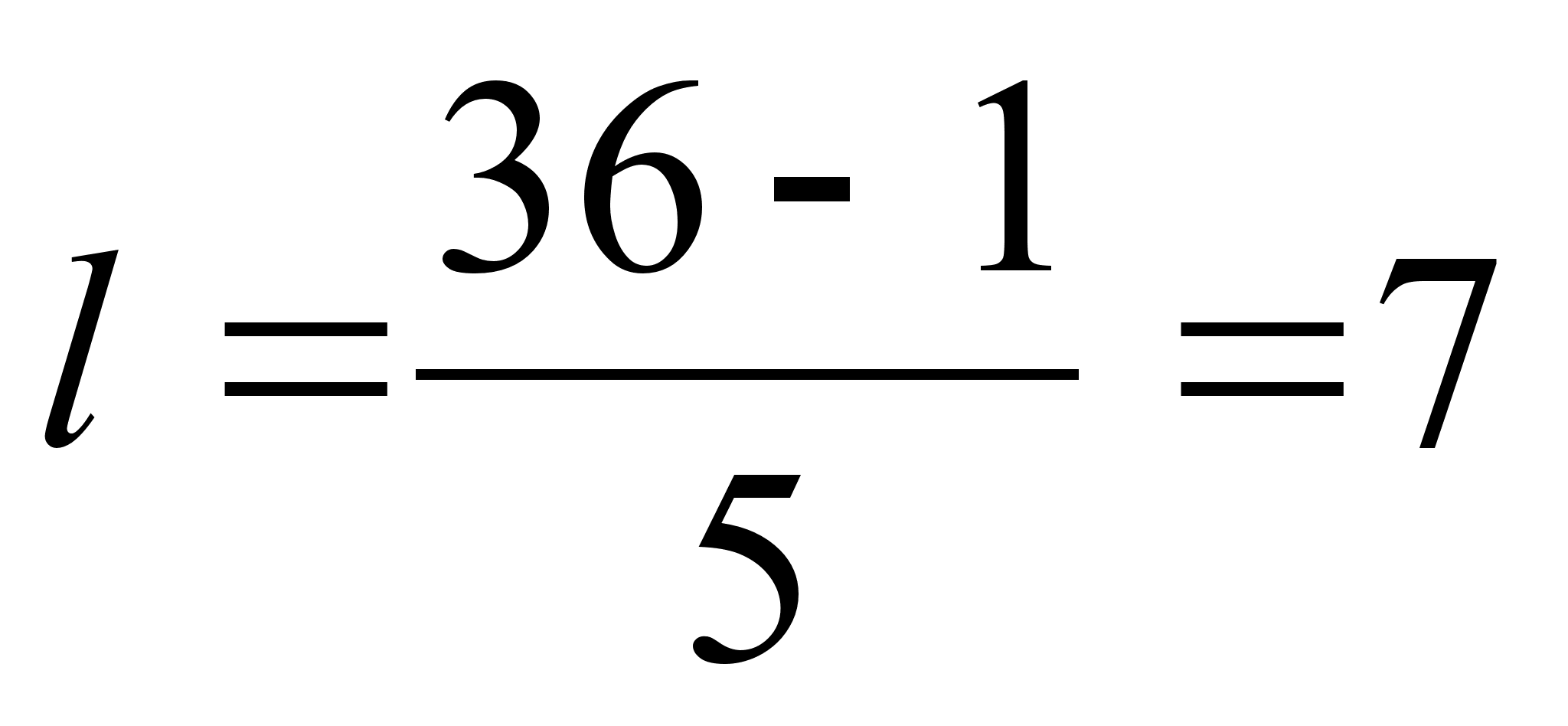
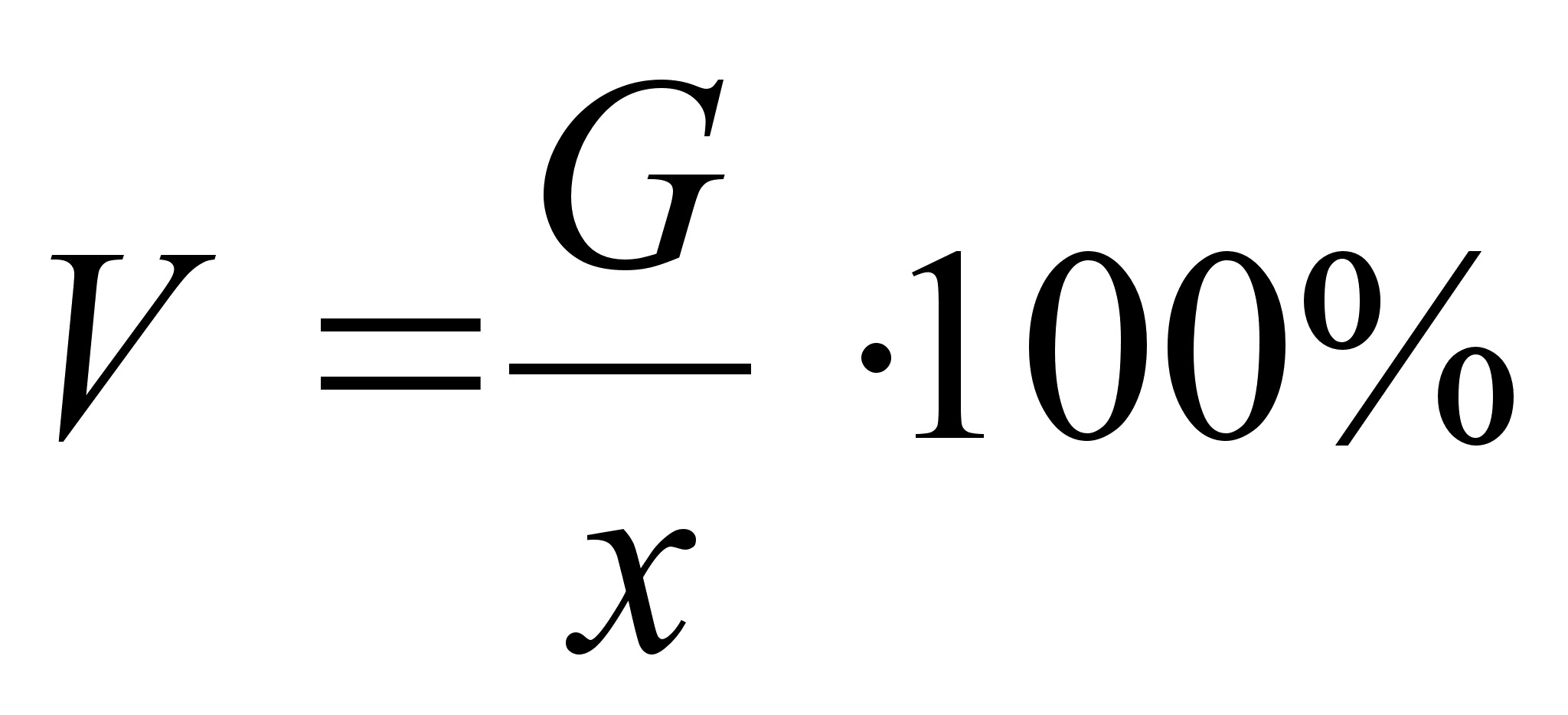
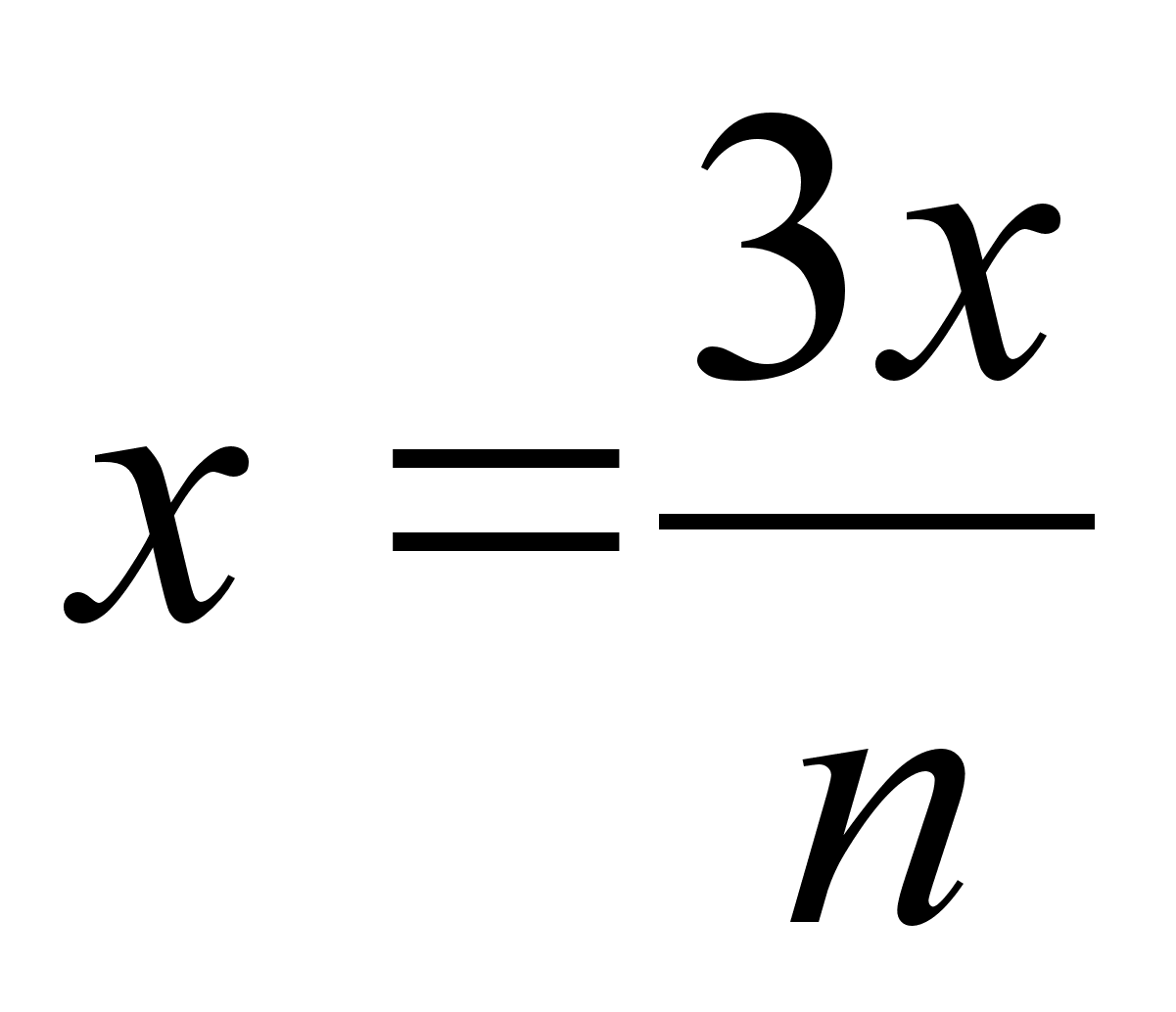
0 комментариев