Навигация
Визначення привідного моменту
22720
знаков
5
таблиц
10
изображений
2.3 Визначення привідного моменту.
Визначаємо привідний момент сили Q для кожного положення механізму:
де : Vci – швидкість повзуна в i-тому положенні механізму.
2.4 Побудова графіків Мпр=ƒ(φ), AQ= ƒ(φ), Ap= ƒ(φ), ΔE= ƒ(φ).
Визначаємо масштабний коефіцієнт
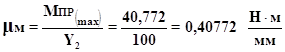
де : Y2 – відстань на осі ординат, відповідна даному приведеному моменту.
Будуємо вісь координат. По осі абсцис відкладаємо кут повороту механізму, та прораховуємо аналогічно як в пункті 1.8. З отриманих точок проводимо промені, на яких відкладаємо приведений момент перерахований в графічний аналог:
З’єднавши отримані точки ми отримуємо графік приведеного моменту від сил Q, МQ= ƒ(φ).
Методом графічного інтегрування графіка приведеного моменту, отримуємо графік робіт сил Q, AQ= ƒ(φ). З’єднавши початок і кінець останнього, отримуємо графік робіт рушійних сил Aр= ƒ(φ). Графічно диференціюючи графік Aр= ƒ(φ), отримуємо графік моментів рушійних сил Мр= ƒ(φ).
Згідно з формулою кінетична енергія дорівнює різниці робіт сил Q і рушійних сил, тобто:
На графіку робіт заміряємо різницю між графіками AQ= ƒ(φ) та Aр= ƒ(φ). Цю різницю наносимо на відповідні промені системи координат. З’єднавши отримані точки отримуємо графік зміни кінетичної енергії ΔE= ƒ(φ).
2.5 Побудова графіка Jпр=ƒ(φ).
Проведемо розрахунок для першого положення механізму.
Визначаємо осьовий момент інерції ланок
, так як довжина ℓ3 змінюється, тому для кожного положення його розраховуємо окремо, а результати заносимо в таблицю № 4.
Визначаємо швидкість центрів мас ланок:
Аналогічно швидкість центрів мас ланок рахуємо і для інших положень механізму, результати зараховуємо в таблицю № 3.
Таблиця №3
|
| Од. вимір. | Положення механізму | |||||||
| 0,8 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| Vs3 | м/с | 0 | 0,72 | 1,44 | 0 | 0,792 | 1,224 | 1,224 | 0,792 |
| Vs4 | м/с | 0 | 0,72 | 1,44 | 0 | 0,72 | 1,008 | 1,008 | 0,72 |
Визначаємо кінетичну енергію механізму:
де: Е1 – кінетична енергія ланки №1;
Е2 – кінетична енергія ланки №2;
Е3 – кінетична енергія ланки №3;
Е4 – кінетична енергія ланки №4;
Е5 – кінетична енергія ланки №5.
Визначаємо приведений осьовий момент інерції:
Результати розрахунків для інших положень механізму проводимо аналогічно, а результати заносимо в таблицю №4.
Таблиця №4
|
| Од. вимір | Положення механізму | |||||||
| 0,8 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| J3 | кг·м2 | 0,4752 | 0,,4752 | 0,4752 | 0,4752 | 0,4752 | 0,4752 | 0,4752 | 0,4752 |
| E1 | Дж | 1,4256 | 1,4256 | 1,4256 | 1,4256 | 1,4256 | 1,4256 | 1,4256 | 1,4256 |
| E2 | Дж | 0 | 1,34639 | 1,51323 | 0 | 0,74287 | 1,7936 | 1,7936 | 0,876 |
| E3 | Дж | 0 | 0,88483 | 0,88422 | 0 | 0,22197 | 0,43224 | 0,37308 | 0,22257 |
| E4 | Дж | 0 | 1,211096 | 1,630886 | 0 | 0,33696 | 0,66044 | 0,56946 | 0,33696 |
| E5 | Дж | 1,9008 | 5,342626 | 5,929136 | 1,9008 | 3,2026 | 4,78208 | 4,63694 | 1,91073 |
| Eмех | Дж | 0,000594 | 0,001669 | 0,001853 | 0,000594 | 0,001008 | 0,001496 | 0,001449 | 0,000597 |
| Jпр | кг·м2 | 64 | 180 | 200 | 64 | 109 | 161 | 161 | 64 |
| (Jпр)гр | мм | 0,004386 | 0,002984 | 0,002984 | 0,004386 | 0,006115 | 0,007278 | 0,007278 | 0,006115 |
Визначаємо масштабний коефіцієнт:
де: Y2 – відстань на осі абсцис відповідаюча даному осьовому моменту.
Перераховуємо усі отримані осьові моменти інерції в графічні аналоги:
Будуємо систему координат. По осі ординат відмічаємо кут повороту механізму, а по осі абсцис на променях проведених з точок кута повороту проводимо графічні аналоги приведеного осьового моменту. З’єднуємо отримані точки і отримуємо графік приведеного моменту Jпр=ƒ(φ).
2.6 Побудова діаграми енергомас.
Будуємо вісь координат. До цієї вісі проводимо промені з графіка приведеного осьового моменту Jпр=ƒ(φ) і зміни кінетичної енергії ΔЕ=ƒ(φ). На перетині відповідних променів отримуємо точки з’єднавши які, отримуємо діаграму енергомас (петля Віттенбауера).
Похожие работы
... , если к нему приложить уравновешивающую силу и моменты. 2.8 Сравним полученные значения Рур, рассчитанные по методу плана сил и методом рычага Жуковского. Вывод: Проведя силовой анализ механизма, определили реакцию опор, нашли уравновешивающую силу, выяснили, что на данный механизм влияют силы инерции. РАЗДЕЛ III Проектирование эвольвентного зубчатого зацепления Задачами ...
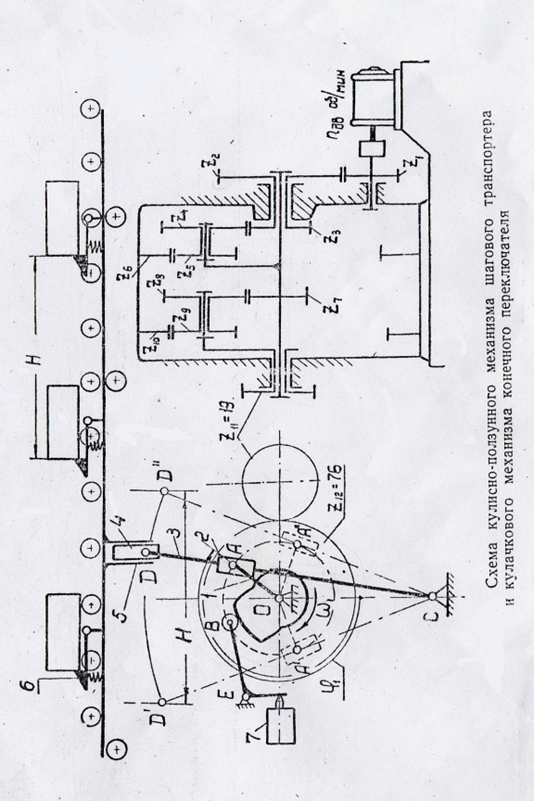
... При графическом изображении физических величин масштаб обозначается буквой с индексом, указывающим, к какой величине он относится. 1. Проектирование основного механизма и определение закона движения 1.1 Проектирование механизма по заданным условиям Механизм шагового транспортера автоматической линии вычерчен в масштабе =50мм/м. Положения начального звена 1 при вращении вокруг центра О ...
... аналогов скоростей рs2 , ps4. Положение механизма. 1 2 3 4 5 6 6’ 7 8 9 10 11 ps2 75 71 70 76 90 110 0 110 103 98 93 84 ps4 42 49 62 93 117 81 0 106 118 96 68 47 1.3 Динамический анализ механизма 1.3.1 Расчет и построение графика приведённого момента сил полезного сопротивления Рассчитаем значение приведённого момента сил полезного сопротивления для ...
... Прод. П/кр. Прод.. Гарантийный срок службы, ч 500 500 500 400 50 25цикл 10 Масса, кг 1,4 2,6 3,0 2,0 1,8 3,5 Технические характеристики Д-0,1 Д-0,16 А Д-5 Д-7 Д-25А Д-25-1С Д-40 Д-50А Д-55 Напряжение питания, В 2,8 4,5 27 27,5 27 27 27 27 27 Номинальный момент •10 4,Н · м 4,9 6,37 41,2 102 399 285 ...
0 комментариев