Навигация
Расчет дифференциала
2.4 Расчет дифференциала
2.4.1 Выбор основных параметров зубчатых колес дифференциалов
Все зубчатые колеса дифференциалов прямозубые. Для конических зубчатых колес симметричного дифференциала внешнее конусное расстояние Re и внешний модуль me = mte можно выбирать в зависимости от расчетного крутящего момента Т на сателлите:
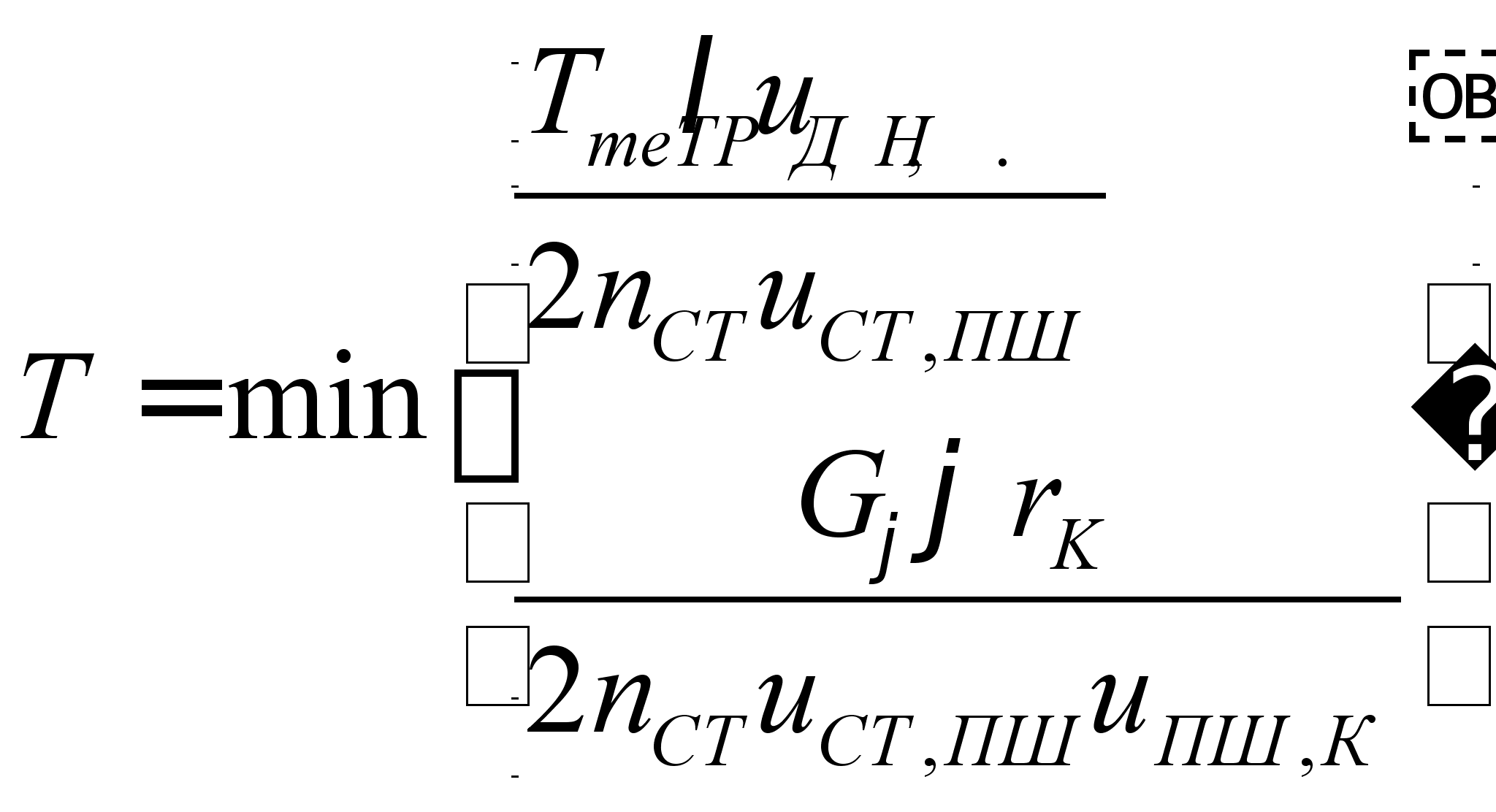 ,
,
где l - доля крутящего момента двигателя, которая поступает на корпус дифференциала, l = 1 [14.c.198];
uтр,д.н – передаточное число трансмиссии от двигателя до корпуса дифференциала при включении низшей передачи в коробке передач, uтр,д.н = 6,58;
nст – количество сателлитов в дифференциале, nст = 4;
uст,пш – передаточное число от сателлита до полуосевой шестерни, uст,пш = 2;
uпш,к – передаточное число от полуосевой шестерни до ведущего колеса автопоезда, uпш,к = 5,00;
 .
.
Согласно [13.c.168] me = 6мм, Re = 70мм.
Определяем число зубьев сателлита
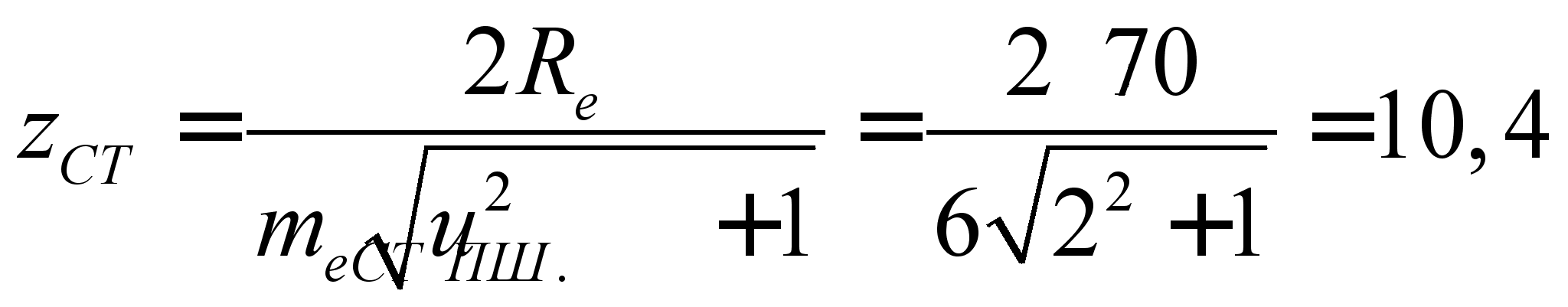 ,
,
так как zст > 10, то согласно [14.c.199] принимаем zст = 11.
Тогда z1 = z2 = zст uст.пш = 11 2 = 22.
Условие сборки и размещения (соседства) имеет вид [14.c.199]
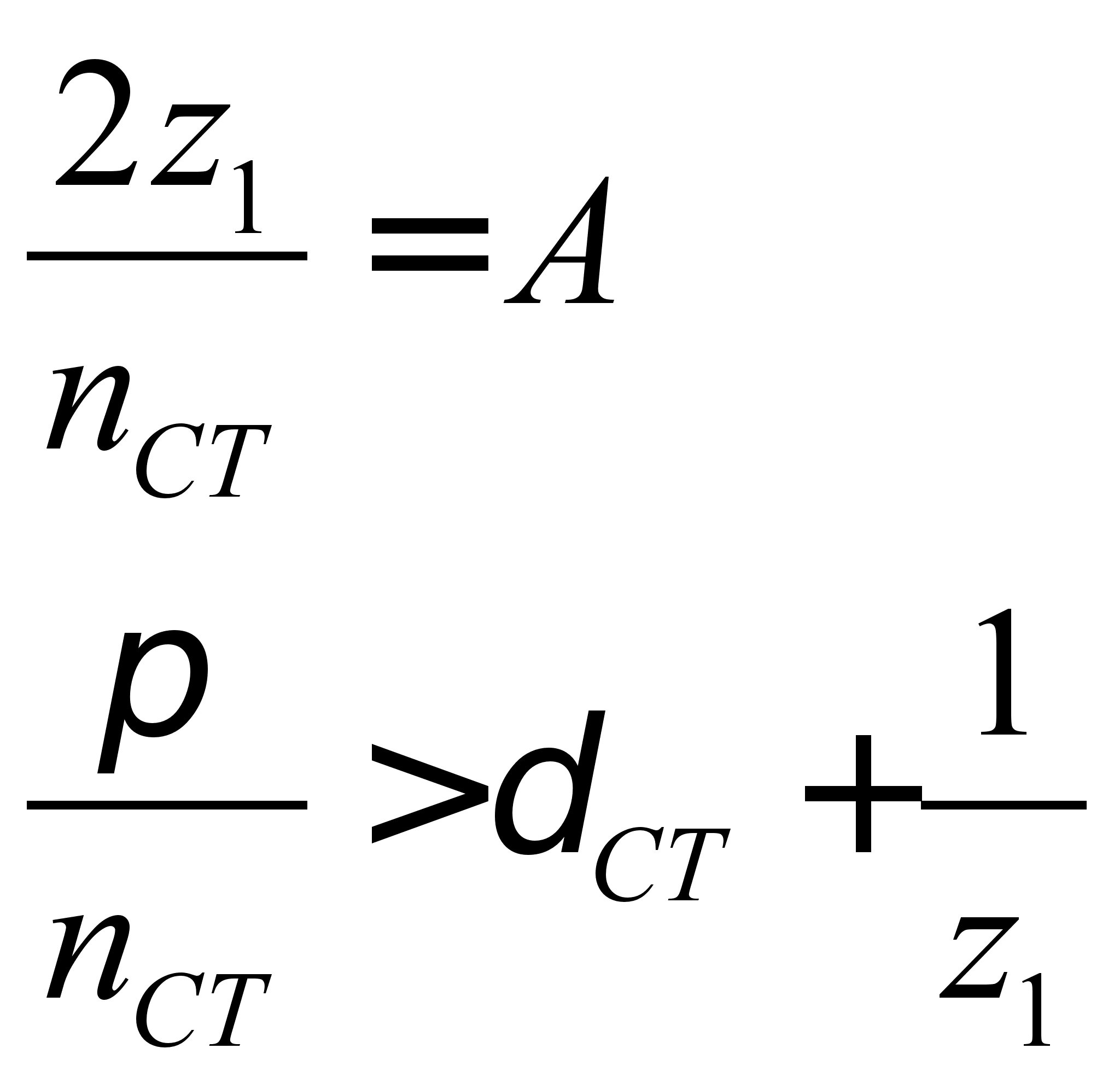 ,
,
где А – целое
число; 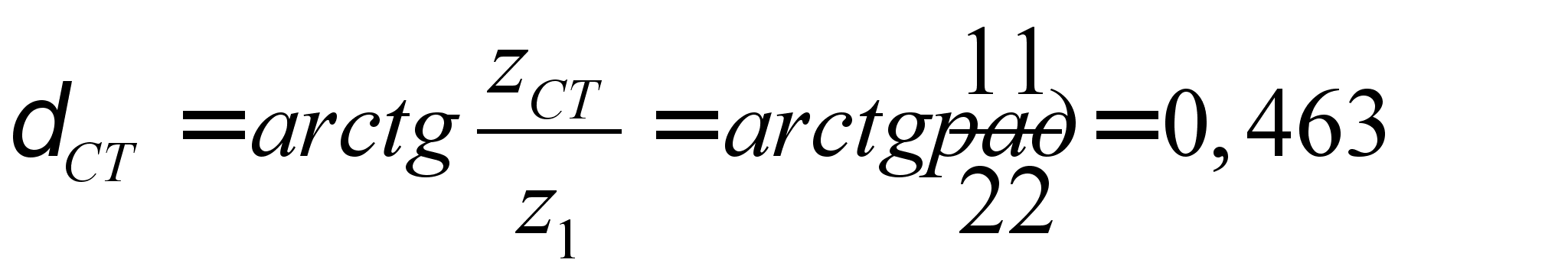
 ,
,
условия выполняются.
Принимаем ширину зубчатого венца b = 0,3Re =0,3 = 21мм,
угол профиля исходного контура a = 22°30ў,
коэффициент высоты головки зуба h*a = 0,8,
коэффициент радиального зазора с* = 0,25,
коэффициент граничной высоты h*l = 1,6.
материал сталь 40XH, термообработка – объемная закалка HRCЭ 45…55.
ПHlimM = 100 МПа,
sFlimM= 1600 МПа.
Коэффициенты смещения исходного контура х для пары конических зубчатых колес принимаем равными по величине и обратными по знаку (у сателлита со знаком плюс), [14.c.199]
 .
.
Коэффициенты изменения толщины зуба хt назначаем также равными по величине и обратными по знаку (у сателлита со знаком плюс), хt = 0,063 [13.c.199].
2.4.2 Расчет на прочность и сопротивление усталости
Зубчатые колеса шестеренчатых дифференциалов на сопротивление усталости не рассчитывают, а рассчитывают только на прочность при воздействии максимального динамического момента Тд на корпус дифференциала. При этом считаем что каждый сателлит передает усилие двумя зубьями.
Максимальный динамический момент на корпусе дифференциала
![]() ,
,
где Т – наибольший крутящий момент на полуоси, Т =7855 Н м.
![]() .
.
Максимальные напряжения
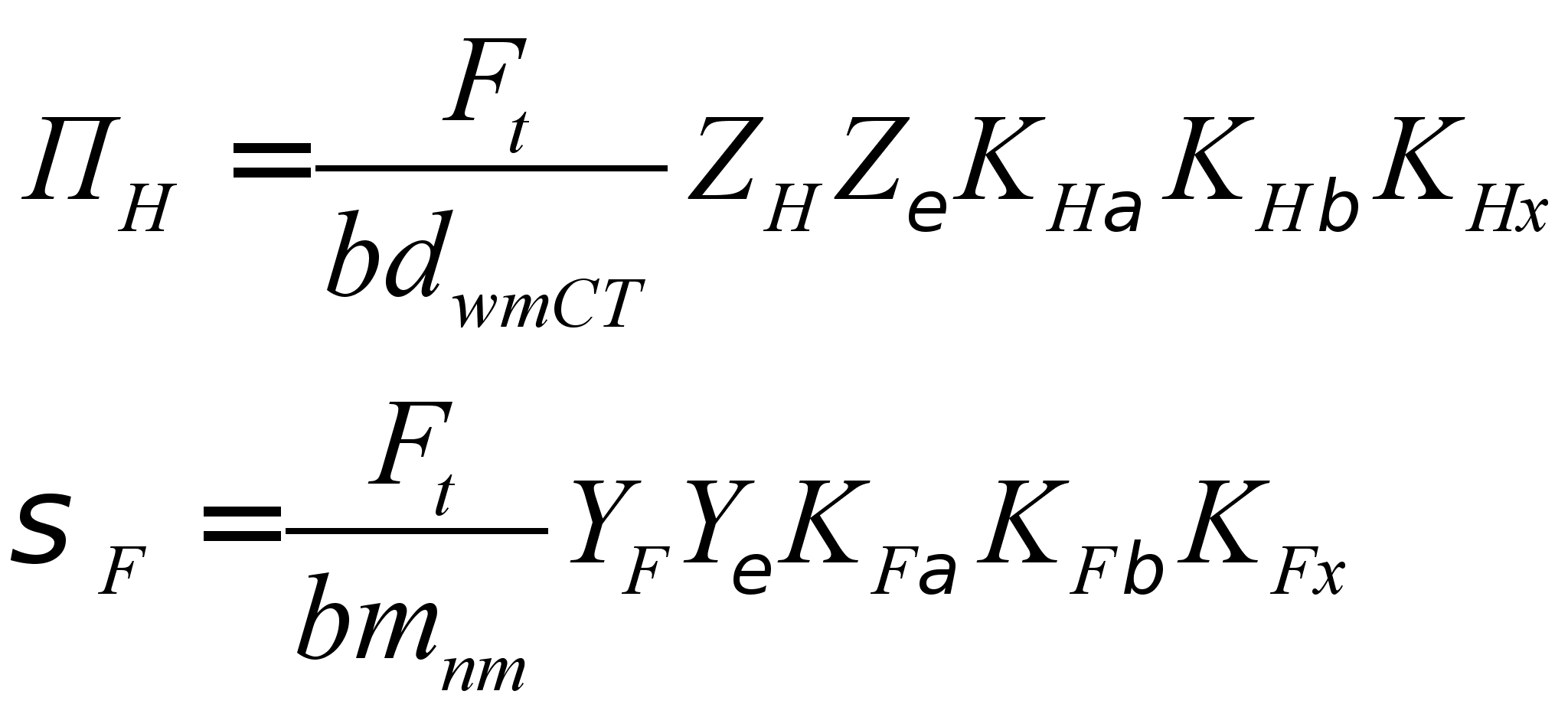 ,
,
где Ft – окружная сила на сателлите,
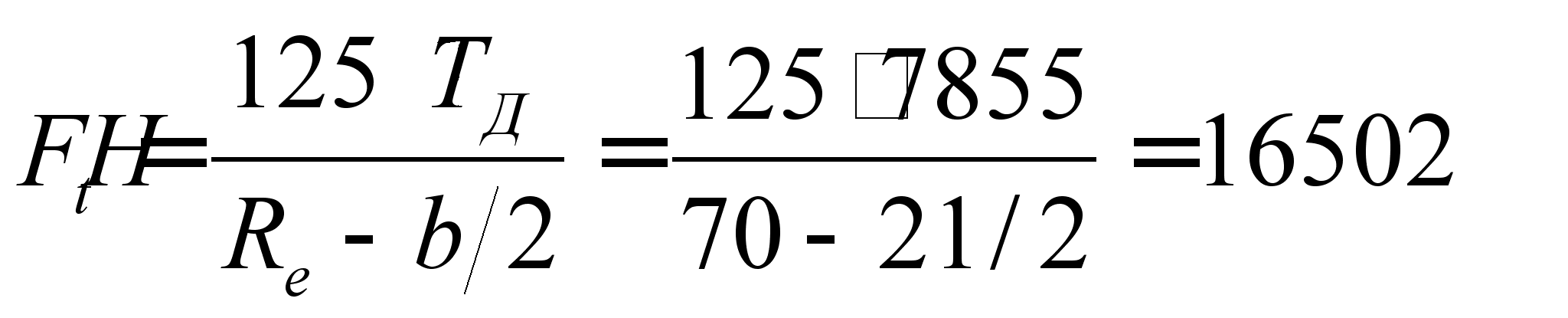 ;
;


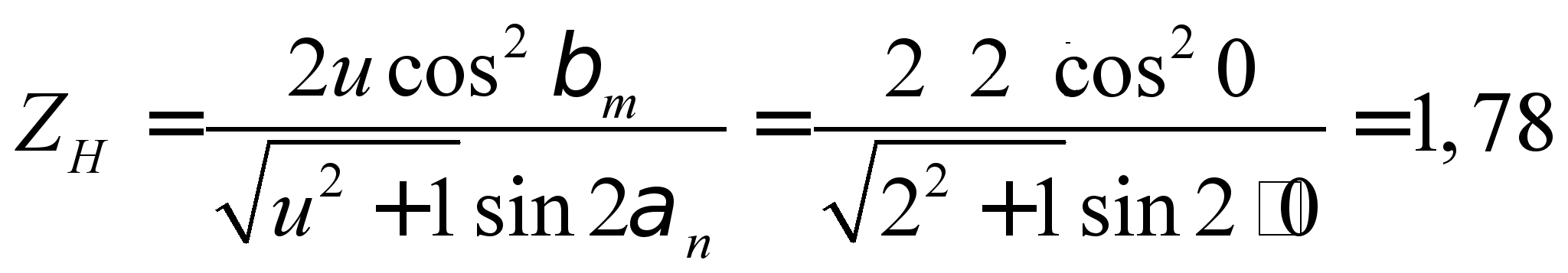 ;
;
Ze = Ye =1,0 [13.c.323];
KHa = 1 [13.c.325];
KHb = 1,02 [13.c.329];
KHx = 1 [13.c.331];
![]() ,[13.c.319]
,[13.c.319]
Y0F = 2,25 [13.c.319];
KИ = 1 [13.c.322];
Ka = 0,935 [13.c.323]
![]() ,[13.c.325]
,[13.c.325]
K0Fa1 = 1,37
K0Fa2 = 1,30 [13.c.326]
KD = 0 [13.c.327]
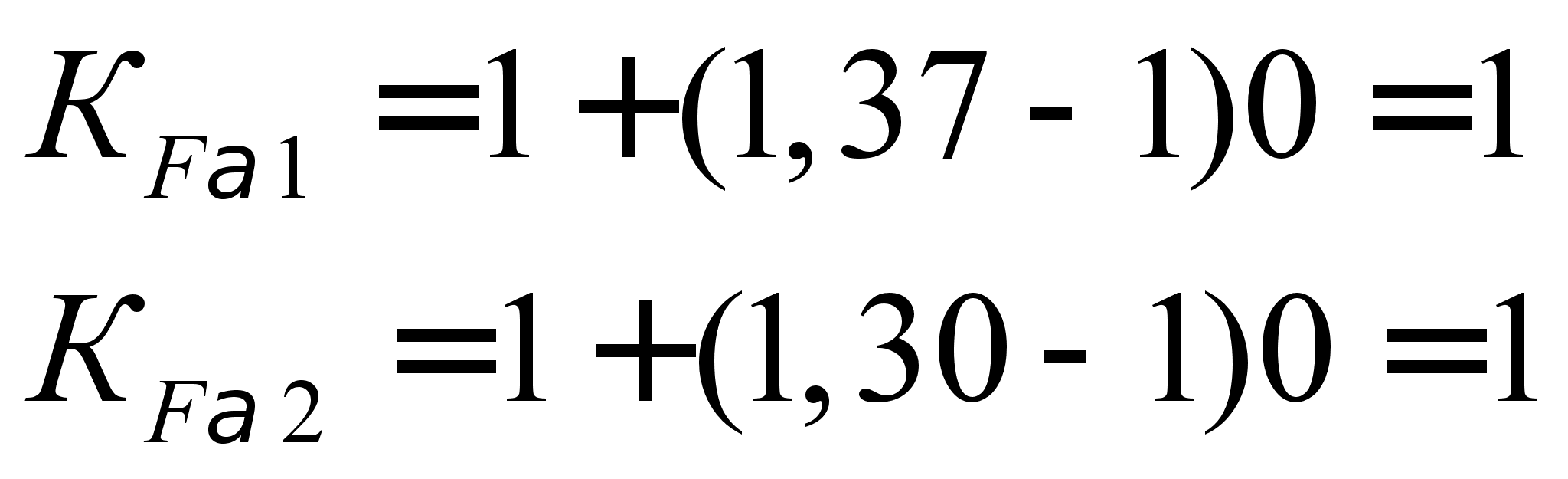
![]() ;
;
![]() =
1,02
[13.c.327];
=
1,02
[13.c.327];
KFw = 1 [13.c.328];
![]() ;
;
Kr = 1,03 [13.c.323];
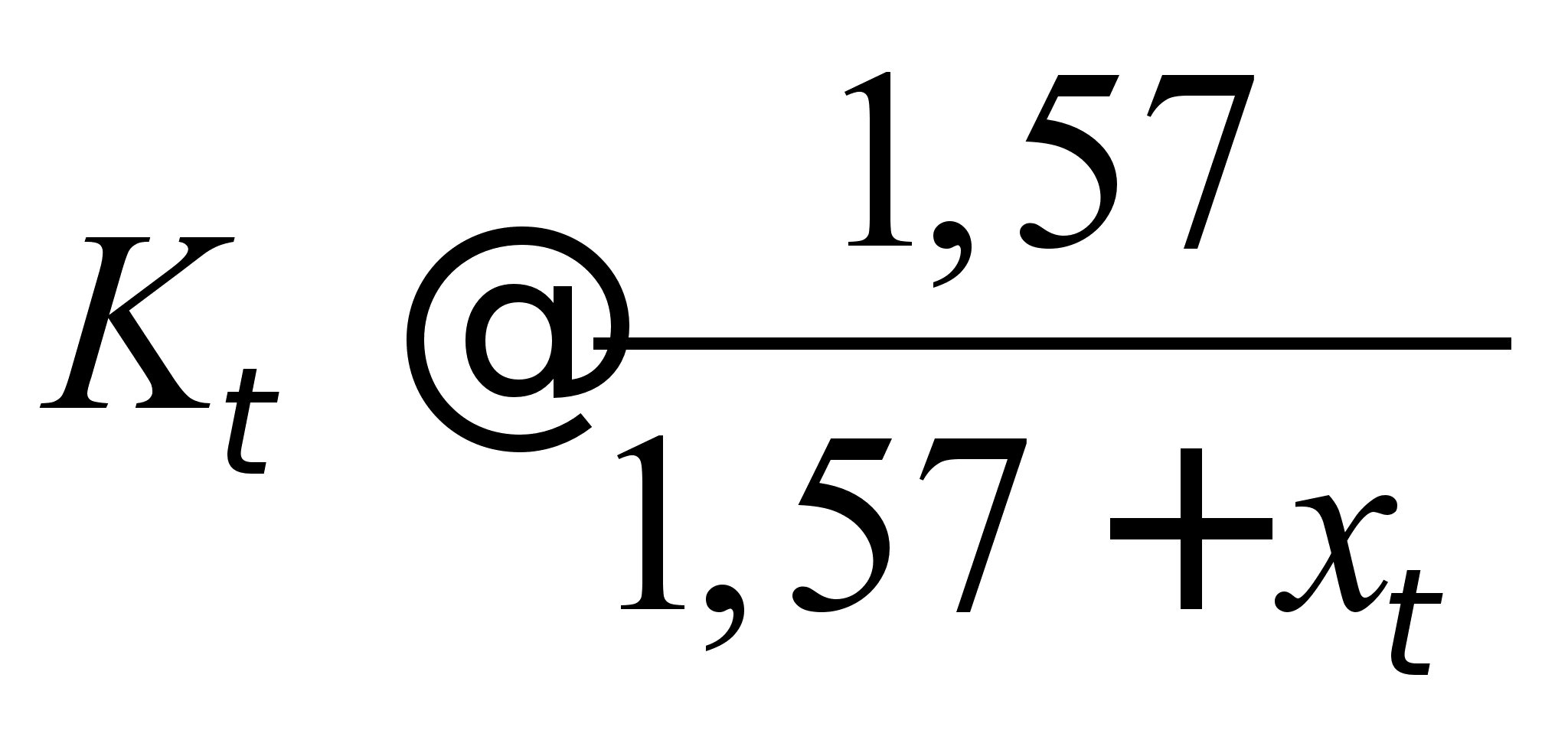 ,[13.c.323]
,[13.c.323]
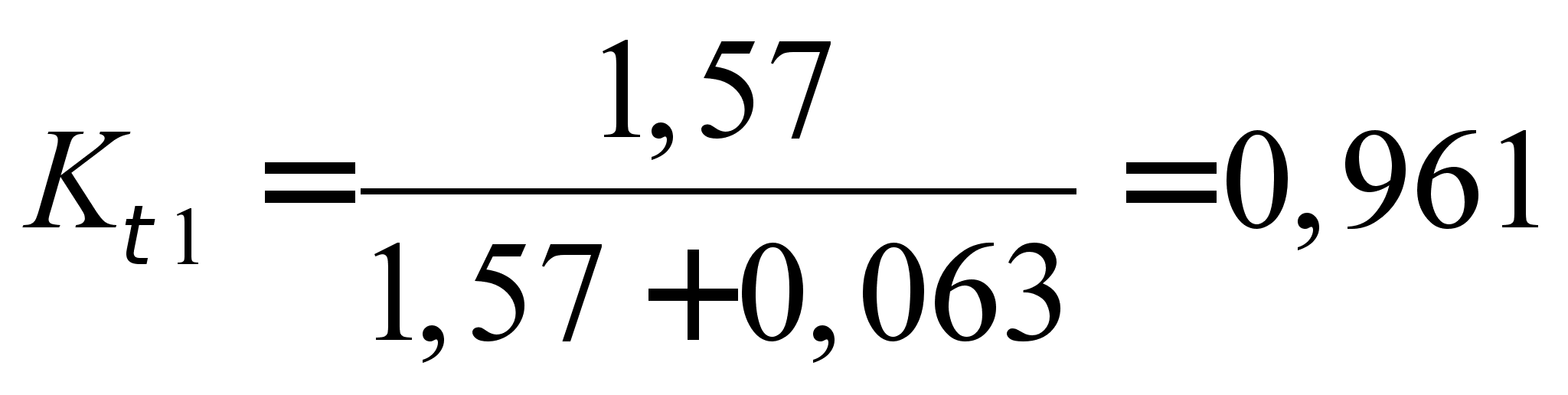
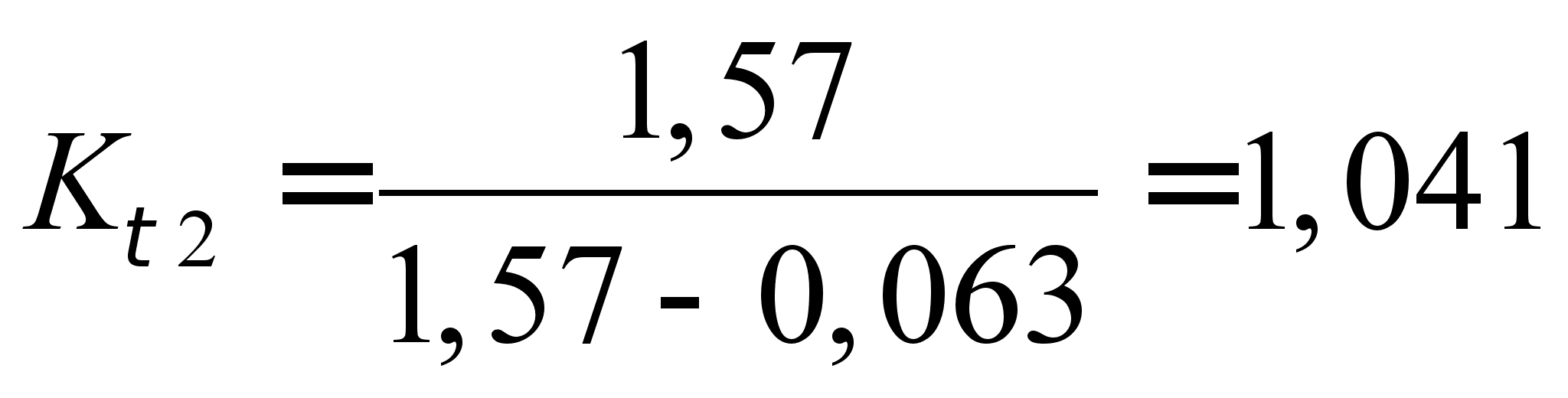
![]()
![]()
KFx = 1[13.c.331].

Условие достаточной прочности зубьев имеет вид
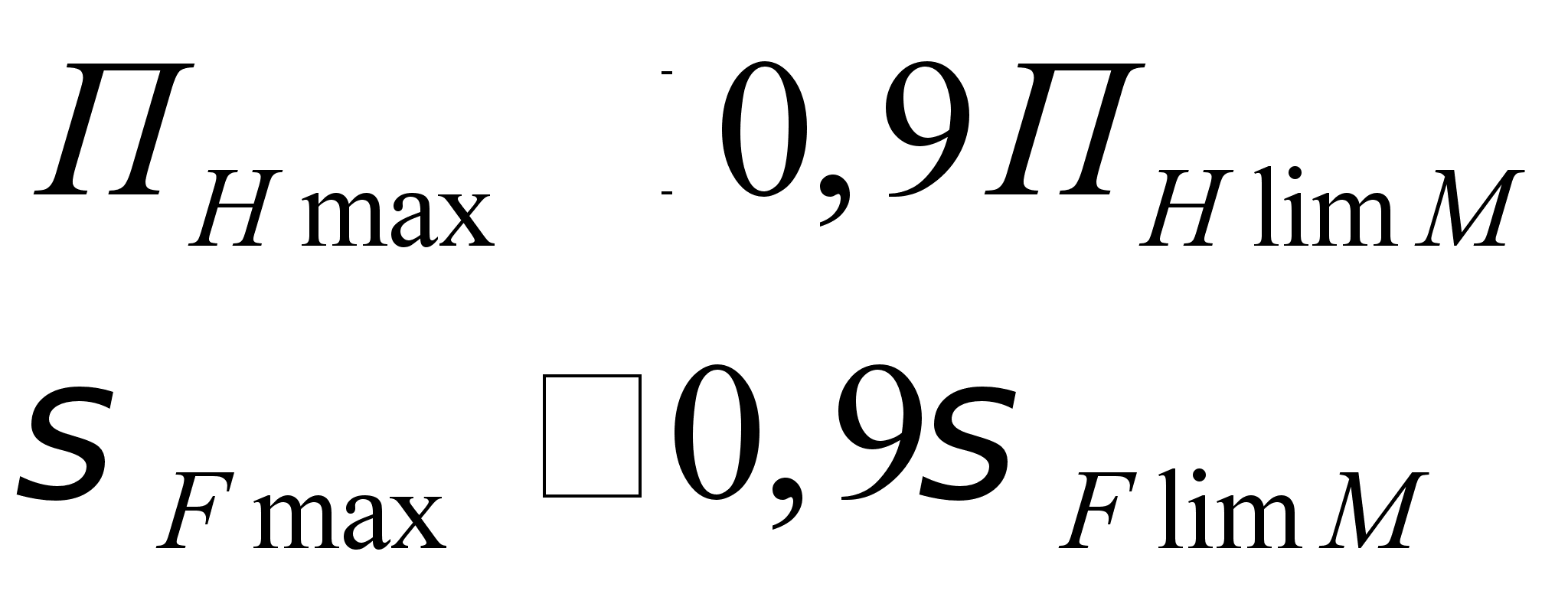
Условие достаточной прочности выполняется.
Похожие работы
... а количество групп значительно меньше. Все это дает возможность своевременно устанавливать экономические сроки службы агрегатов. [1] 3.2 Результаты установленной структуры и объемов плановых замен Для осуществления расчетов необходима информация: стоимость новых деталей для замены (приложение Г), нормы трудоемкости на проведение работ (приложение Д); тарифные ставки для соответствующих ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
... -12рк (ТУ 38.101844-80). ТАД-17И (класс 18) получают смешением остаточного и дистиллятного масел с введением многофункциональной и депрессорной присадок. Масло обладает высокими эксплуатационными свойствами, является универсальным и может применяться в тяжелонагруженных цилиндрических, спирально-конических и гипоидных передачах грузовых и легковых автомобилей в умеренной и жаркой климатических ...





0 комментариев