Навигация
Потери напора по длине
5.6. Потери напора по длине
При установившемся движении реальной жидкости основные параметры потока: величина средней скорости в живом сечении (v) и величина перепада давления![]() зависят от физических свойств, движущейся жидкости и от размеров пространства, в котором жидкость движется. В целом, физические свойства жидкости определяются через размерные величины, называемые физическими параметрами жидкости.
зависят от физических свойств, движущейся жидкости и от размеров пространства, в котором жидкость движется. В целом, физические свойства жидкости определяются через размерные величины, называемые физическими параметрами жидкости.
Можно установить взаимосвязь между всеми параметрами, от которых зависит движение жидкости. Условно эту зависимость можно записать как некоторую функцию в неявном виде.
![]()
где: ![]() - линейные величины, характеризующие трёхмерное
- линейные величины, характеризующие трёхмерное
пространство,
![]() - линейная величина, характеризующая состояние стенок канала (шероховатость), величина выступов,
- линейная величина, характеризующая состояние стенок канала (шероховатость), величина выступов,
![]() - средняя скорость движения жидкости в живом сечении потока,
- средняя скорость движения жидкости в живом сечении потока,
![]() - разность давления между начальным и конечном живыми сечениями потока (перепад давления),
- разность давления между начальным и конечном живыми сечениями потока (перепад давления),
![]() - удельный вес жидкости,
- удельный вес жидкости,
- плотность жидкости,
- динамический коэффициент вязкости жидкости,
![]() - поверхностное натяжение жидкости, К - модуль упругости жидкости.
- поверхностное натяжение жидкости, К - модуль упругости жидкости.
Для установления зависимости воспользуемся выводами так называемой![]() -теоремы. Суть её заключается в том, что написанную выше зависимость, выраженную в неявном виде, можно представить в виде взаимозависимых безразмерных комплексов. Выберем
-теоремы. Суть её заключается в том, что написанную выше зависимость, выраженную в неявном виде, можно представить в виде взаимозависимых безразмерных комплексов. Выберем
три основных параметра с независимыми размерностями![]() , остальные парамет-
, остальные парамет-
ры выразим через размерности основных параметров.
Эта операция выполняется следующим образом: пусть имеется некоторый параметр i, выразим его размерность через размерности основных параметров; это будет означать:
![]() ?
?
т.е. размерности левой и правой частей равенства должны быть одинаковыми. Тогда можно записать:
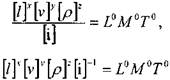
Полученные в результате такой операции безразмерные параметры будут называться пи-членами. Эти безразмерные комплексы имеют глубокий физический смысл, они представляют собой критерии подобия различных сил, действующих в тех или иных процессах.
Проделаем такую операцию с некоторыми из параметров.
Параметр А.
![]() i
i
Теперь запишем показательные уравнения по размерностям последовательно в следующем порядке: L (длина), М (масса), и Т (время):
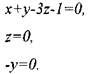
Из этой системы уравнений: ![]() Таким образом, безразмерным
Таким образом, безразмерным
комплексом по этому параметру может быть:![]() Параметр у.
Параметр у.
![]() >* ' откуда получим:
>* ' откуда получим:
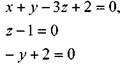
и найдём: ![]() . Таким образом, безразмерным комплексом по
. Таким образом, безразмерным комплексом по
этому параметру может быть: ![]() . Эта безразмерная величина называется
. Эта безразмерная величина называется
числом Фруда, Fr. Параметр /и.
![]()
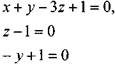
и найдём:![]()
![]()
Полученный безразмерный комплекс называется числом Рейнольдса, Re. Выполняя аналогичные операции с остальными параметрами можно найти:
![]() число Эйлера, число Вебера, We.
число Эйлера, число Вебера, We.
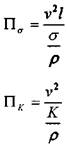 число Коши, Са. В итоге получим как результат:
число Коши, Са. В итоге получим как результат:
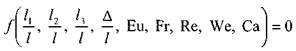
Поскольку, в большинстве случаев силами поверхностного натяжения можно пренебречь, а жидкость считать несжимаемой средой, можно упростить запись предыдущего выражения, решив последнее уравнение относительно Ей:
![]()
Считая канал круглой цилиндрической трубой, и принимая![]() , получим:
, получим:
![]()
Множитель был вынесен за скобки ввиду того, что потери напора по длине пропорциональны длине канала конечных размеров. Далее учитывая, что:![]() , получим:
, получим:
![]()
Обозначим: ![]() Эту величину принято называть коэффициен-
Эту величину принято называть коэффициен-
том сопротивления трения по длине или коэффициентом Дарси. Окончательно для круглых труб, учитывая, что![]() :
:
![]()
Эта формула носит название формулы Дарси-Вейсбаха и является одной из основных формул гидродинамики.
Коэффициент потерь напора по длине будет равен:
![]()
Запишем формулу Дарси-Вейсбаха в виде:
![]()
Величину![]() называют гидравлическим уклоном, а величину
называют гидравлическим уклоном, а величину![]() называ-
называ-
ют коэффициентом Шези.
![]()
Величина ![]() имеет размерность скорости и носит название динамической
имеет размерность скорости и носит название динамической
скорости жидкости.
Тогда коэффициент трения (коэффициент Дарси):![]()
' ' 6. Режимы движения жидкости
Похожие работы
... и никто в России не отдавал себе отчета и не имел ясного представления о том, как работает вообще мировая политическая мысль и каким образом вообще совершаются мировые события. Дипломатия, политика в лучшем случае рисовались как система известных навыков и приемов, присущих дипломатическим канцеляриям. Оценка дипломатического таланта и умения сводилась к признанию известной сноровки и ловкости в ...
праведливы соотношения ... Пусть высота тетраэдра равна ... . Тогда его объём равен ... . Воспользуемся вторым законом Ньютона и со- ставим уравнение движения тетраэдра: ... ... где ... - ускорение центра масс тетраэдра. Переходя к пределу (устремляя ... ), получим ... Получим формулу Коши, утверждающую, что напряжения на гранях образуют систему взаимно уравновешенных ...
... самоиндукции и экстратоки замыкания и размыкания. Открытие явления электромагнитной индукции сразу же приобрело огромное научное и практическое значение; оно легло в основу электротехники. Работам Фарадея в области электричества положило начало исследование так называемых электромагнитных вращений. Из серии опытов Эрстеда, Араго, Био, Савара, проведенных в 1820 г., стало известно не только об ...
... фундамента. 59 Нормативный срок службы водозаборной арматуры, годы: А) 5; В) 10; С) 15; D) 20; E) 25. 60 Нормативный срок службы чугунных радиаторов, годы: А) 5; В) 10; С) 20; D) 30; E) 40. 61 Какой параметр ограничивается во всех инженерных системах? A) давление; B) скорость; C) температура; D) вязкость; E) расход. 62 Какая инженерная система рассчитывается для трех различных ...

0 комментариев