Равновесие твёрдого тела в жидкости

2.8. Равновесие твёрдого тела в жидкости

Определим силу давления на твёрдое тело, погружённое в жидкость. На замкнутую криволинейную поверхность, являющуюся поверхностью твердого тела погружённого в

жидкость будут действовать массо­вые силы (в данном случае силы тя­жести) и поверхностные, силы дав­ления на поверхность тела. Рассмот­рим действие сил давления. Как из­вестно, горизонтальные составляю­щие силы давления будут взаимно уравновешены. Так как проекции тела на координатную плоскость XOZ с его левой и правой сторон 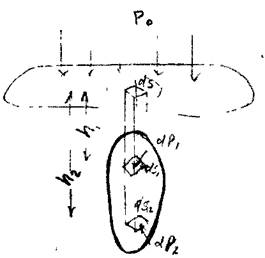 совпадут; то совпадут и координаты центров тяжести этих проекций. То­гда проекции сил давления на ось

ОХ будут одинаковыми по величине, но противоположными по направлению Аналогично можно записать и для проекций сил давления на ось OY (давление на проек­ции поверхностей в координатной плоскости YOZ),. Неуравновешенными будут

лишь вертикальные составляющие силы давления, действующие на верхнюю и нижнюю стороны поверхности тела.

Вертикальными сечениями выделим на верхней и нижней половинах тела малые площадки. Тогда вертикальные составляющие на верхнюю и нижнюю площадки будут равны:

После интегрирования по объёму тела найдём равнодействующую сил давления. Она окажется равной разности весов двух тел давления, ограниченных свободной поверхно­стью жидкости и верхней и нижней поверхностями тела.

Равнодействующая сил давления носит название выталкивающей силы, эта сила на­правлена вертикально вверх и численно равна весу жидкости в объёме вытесненной те­лом. Последнее положение получило название закона Архимеда. Закон Архимеда часто формулируют несколько иначе: «тело, погружнное в жидкость теряет в своём весе столько сколько весит вытесненная им жидкость».

Таким образом, На погружённое в жидкость тело действуют две силы:

вес телаи выталкивающая сила

ЕслиТело будет тонуть.

ЕслиТело будет всплывать до тех пор пока вес тела и величина

выталкивающей силы, действующей на погруженную часть объёма тела не уравновесятся.

ЕслиТело будет находиться во взвешенном состоянии в жидкости,

т.е. плавать внутри жидкости на любой заданной глубине.

Для тела плавающего на поверхности жидкости должно, таким образом выполняться условие:

Другими словами, степень погружения плавающего на поверхности тела под уровень жидкости заваисит от со­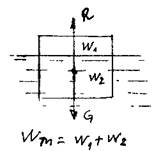 отношения плотности телаи жидкости:

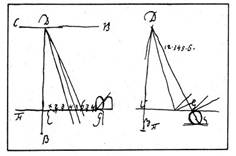
Если тело однородное, то точка приложения силы тяжести тела и точка приложения выталкивающей силы совпадают. В тех случаях, когда плавающее на поверхности жидко­сти тело не однородно по своему составу (корабль с грузом) в условиях равновесия точки приложения действующих на тело сил располагаются в разных местах на прямой верти­кальной линии. В таких случаях на плавающее в жидкости тело действует пара сил, от

действия которой зависит положение тела относительно жидкости Такие плавающие тела могут находиться в ос­тойчивом и не остойчивом состоянии Так тело 1 под дей­ствием пары сил находится в состоянии равновесия На тело 2 действует пара сил, стремящаяся уменьшить угол крена (угол между осью плавания тела и плоскостью сво­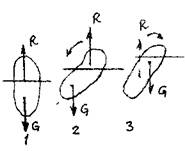 бодной поверхности жидкости) Такое положение пла­вающего тела называется остойчивым На тело 3 действует пара сил, стремящаяся увели­чить угол крена (перевернуть тело), такое положение тела называется не остойчивым по­ложением

^;  t* 3. Элементы кинематики жидкости

Кинематикой называют раздел механики, изучающий движение физических тел во­обще, вне связи с источником движения (силами). Это определение справедливо и для ки­нематики жидкости как отдельного раздела гидравлики. 3.1. Методы изучения движения жидкости.

Жидкость представляет собой физическое тело, состоящее из бесконечно большого числа бесконечно малых частиц. С большой степенью точности мы можем рассматривать жидкое тело как сплошную среду, эта модель позволяет значительно упростить решение большинства гидравлических задач. Тем не менее, нередки случаи, когда уровень иссле­дования движения жидкого тела требует глубокого знания физических процессов проис­ходящих в движущейся жидкости на молекулярном уровне. В таких случаях вполне удоб­ная модель сплошной среды может оказаться неприемлемой.

Исходя из практики изучения гидравлики как прикладной дисциплины, можно упо­мянуть два метода изучения движения жидкости: метод Лагранжа и метод Эйлера.

Описание движения жидкости методом Лагранжа сво­дится к рассмотрению положения частиц жидкости (в пол­ном смысле слова) в любой момент времени. Так в началь­ный момент времени частицы находились в точках 1, 2, 3 и 4. По истечении некоторого времени они переместились в точки: Г, 2',3'и4', причём это перемещение сопровожда­лось изменением объёмов и форм частиц (упругой деформа­цией). Тогда можно утверждать, что частицы жидкости при 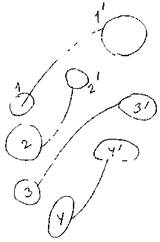 своём движении участвуют в трёх видах движения (поступа­тельном, вращательном и деформации). Для описания такого сложного движения жидко­сти необходимо, таким образом, определить как траектории частиц, так и гидравлические характеристики частиц (плотность р, температуру Т и скорость и) в функции времени и координат.

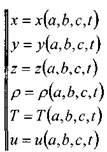
Переменные а, Ь, с, и / носят название переменных Лагранжа. Задача сводится к ре­шению систем дифференциальных уравнений в частных производных для каждой части-

цы жидкости. Метод Лагранжа ввиду громоздкости и трудности решения может исполь­зоваться в случаях детального изучения поведения лишь отдельных частиц жидкости. Ис­пользование этого метода для инженерных расчётов не рентабельно.

Суть другого метода, метода Эйлера заключается в том, что движение жидкости подменяется изменением поля скоростей. Под полем скоростей понимают некоторую дос­таточно большую совокупность точек бесконечного пространства занятого движущейся жидкостью, когда в каждой точке пространства в каждый момент времени находится час­тица жидкости с определённой скоростью (вектором скорости). Припишем неподвижным точкам пространства скорость частиц жидкости, которые в данный момент времени нахо­дятся в этих точках. Поскольку пространство бесконечно и непрерывно, то мы имеем мас­сив данных о скоростях достаточно полный, чтобы определить (задать) поле в каждой его точке. Условно, нос достаточной точностью такое поле можно считать непрерывным.

Несмотря на то, что исходные условия создания модели движущийся жидкости до­вольно сложные, тем не менее, метод Эйлера весьма удобен для расчётов.

Построение поля скоростей осуществляет­ся следующим образом:

На некоторый момент времени (например, to) произвольным образом выберем необходимое число точек, в которых находятся частицы жид­кости. Приписав их скорости  точкам неподвижного про­странства (1, 2, 3, 4, 5 и 6) мы сделаем «момен­тальную фотографию» поля скоростей на вы­бранный момент времени. В следующий момент времени в тех же выбранных точках

неподвижного пространства будут находиться другие частицы жидкости, имеющие другие ско­рости . Выполнив уже

известную процедуру второй раз, получим но­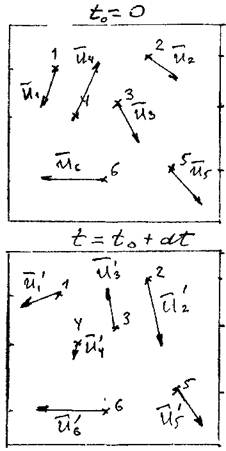 вую «моментальную фотографию» поля скоро­стей на момент времени. Теперь вместо изучения траекторий частиц жидкости

будем сравнивать поля скоростей. Тогда система уравнений примет вид:

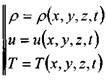
Поле скоростей движения жидкости иногда называют гидродинамическим полем по аналогии с электромагнитным, тепловым и др. полями. Это определение не противоречит физической стороне процесса движения жидкости. Анализируя состояние гидродинами­ческого поля на разные моменты времени, можно отметить, что с течени­ем времени поле изменилось, несмотря на то, что в отдельных точках 5 и 6 скорости оста­лись постоянными Такое поле называют нестационарным гидродина­мическим полем. В частном случае, когда во всех точках неподвижного пространства с течением времени предыдущие частицы жидкости сменяются другими с такими же скоро­стями, то поле скоростей во времени не меняется. Такое гидродинамическое поле называ­ют стационарным. В соответствии с этим различают и два вида движения жидкости: уста­новившееся, когда поле скоростей является стационарным и неустановившееся при неста­ционарном гидродинамическом поле.

3.2.Кинематические элементы движущейся жидкости

Основной кинематической характеристикой гидродинамического поля является ли­ния тока - кривая, в каждой точке которой вектор скорости направлен по касательной к кривой. И ходя из данного определения можно записать дифференциальное уравнение линии  тока:

Если через некоторую неподвижную в пространстве кривую провести линии тока, то полученная поверхность называется поверхностью тока, а образованное этой поверхно­стью тело будет называться трубкой тока. Жидкость, на­полняющая трубку тока, называется элементарной струйкой. Поскольку линии тока никогда не пересекают­ся, то поверхность трубки тока является непроницаемой 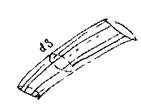 внешней границей для элементарной струйки жидкости. Сечение трубки тока, нормальное к линиям тока называется живым сечением элементар­ной струйки dS. При установившемся движении жидкости понятия линии тока и траекто­рии движения частицы жидкости совпадают. Объём жидкости протекающий через живое

сечение элементарной струйки в единицу времени называется расходом элементарной струйки.

 ?

где:  объём жидкости, протекающий через живое сечение трубки тока за

время

 расход жидкости в живом сечении трубки тока. Размерность расхода жидкости в системе СИ -м/с.

Гидродинамическое поле считается потенциальным (безвихревым), если в этом поле отсутствует вихревое движение жидкости. В потенциальном поле может существовать лишь поступательное или криволинейное движение жидкости. 3.3 Уравнение неразрывности жидкости

Если в гидродинамическом поле отсутствуют вихри, то; для такого поля можно за­писать уравнение, связывающее параметры движущейся жидкости (плотность жидкости) с

параметрами, характеризующими условия движения жидкости. Вывод такого уравне­ния основан на представлении жидкости как сплошной непрерывной среды, в силу чего такое уравнение получило название уравнения неразрывности.

Для этой цели выделим в пространст­ве малый элемент жидкой среды в виде па­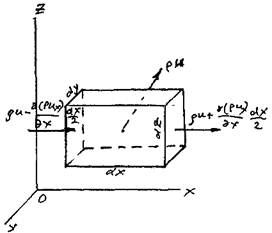 раллелепипеда, стороны которого будут равны соответственно.. Грани

параллелепипеда пусть будут параллельны координатным плоскостям. В центре элемента в данный момент времени будет находиться частица жидкости, плотность которой равна р, а вектор скорости движения и направлен таким образом, что жидкость втекает внутрь элемента через левую, нижнюю и переднюю грани элемента и вытекает через противопо­ложные грани. Будем считать также, что размер элемента достаточно мал, и можно допус­тить, что в пределах этого элемента изменение плотности жидкости и скорости её движе­ния будет прямо пропорционально расстоянию от центра элемента. Одновременно разме­ры граней будут достаточно велики по сравнению с точкой, что позволит утверждать, что плотность жидкости и скорость во всех точках граней будут одинаковыми, как и плот­ность жидкости в пределах соответствующих граней. Тогда произведение плотности жид­кости на вектор скорости (импульс) в специальной литературе часто называют вектором

массовой скорости ри.

В таком случае проекция вектора массовой скорости в центре левой грани элемента на ось ОХ будет равна:

а проекция вектора массовой скорости в центре правой грани элемента на ось ОХ:

 &

Масса жидкости, поступившая через левую грань элемента за малый интервал времени dt\

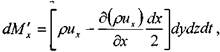
масса жидкости, вытекшая через правую грань элемента за малый интервал времени dt:

Изменение массы жидкости внутри элемента при движении жидкости вдоль оси ОХ:

Аналогично, изменение массы жидкости внутри элемента при движении жидкости вдоль оси OY: 1,

и вдоль оси OZ:

Окончательно, изменение массы жидкости внутри элемента при движении жидкости в произвольном направлении:

 ? или

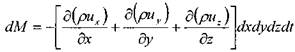
Величина плотности жидкости в начальный момент (до начала движения жидкости t = Q) - р, а по истечении бесконечно малого интервала времени (т.е.

Масса жидкости в объёме выделенного элемента в начальный момент времени:

для времени:

Изменение массы жидкости за бесконечно малый интервал времени dt:

 •> или:

 i

откуда для наиболее общего случая нестационарного полядифференциальное

уравнение неразрывности запишется в следующем виде:

и для частного случая - стационарного поля:

 «

В векторной форме уравнения неразрывности жидкости запишутся в следующем ви­де:

 ?

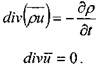Похожие работы

Б.А. Бахметев дипломат, политик, мыслитель

Скачать

124283

0

0

... и никто в России не отдавал себе отчета и не имел ясного представления о том, как работает вообще мировая политическая мысль и каким образом вообще совершаются мировые события. Дипломатия, политика в лучшем случае рисовались как система известных навыков и приемов, присущих дипломатическим канцеляриям. Оценка дипломатического таланта и умения сводилась к признанию известной сноровки и ловкости в ...

Лекции по физике

Скачать

118786

4

0

праведливы соотношения ... Пусть высота тетраэдра равна ... . Тогда его объём равен ... . Воспользуемся вторым законом Ньютона и со- ставим уравнение движения тетраэдра: ... ... где ... - ускорение центра масс тетраэдра. Переходя к пределу (устремляя ... ), получим ... Получим формулу Коши, утверждающую, что напряжения на гранях образуют систему взаимно уравновешенных ...

Исследование работ Фарадея по электричеству

Скачать

166869

1

15

... самоиндукции и экстратоки замыкания и размыкания. Открытие явления электромагнитной индукции сразу же приобрело огромное научное и практическое значение; оно легло в основу электротехники. Работам Фарадея в области электричества положило начало исследование так называемых электромагнитных вращений. Из серии опытов Эрстеда, Араго, Био, Савара, проведенных в 1820 г., стало известно не только об ...

Инженерные системы

Скачать

120331

21

16

... фундамента. 59 Нормативный срок службы водозаборной арматуры, годы: А) 5; В) 10; С) 15; D) 20; E) 25. 60 Нормативный срок службы чугунных радиаторов, годы: А) 5; В) 10; С) 20; D) 30; E) 40. 61 Какой параметр ограничивается во всех инженерных системах? A) давление; B) скорость; C) температура; D) вязкость; E) расход. 62 Какая инженерная система рассчитывается для трех различных ...