Элементы теории подобия

14. Элементы теории подобия

Решение задач гидравлики аналитическими методами на базе дифференциальных уравнений и различных методов математического анализа не нашло широкого примене­ния для практических целей. Необходимость ввода различных допущений и ограничений позволяют использовать полученные строгие решения лишь как качественные оценки изучаемых процессов. Практические же результаты, как правило, достигаются экспери­ментальными методами исследований. Построение модели того или иного процесса также связано с немалыми трудностями. Это, прежде всего, необходимость точного знания фи­зической стороны изучаемого процесса, умение выделить существенные стороны и фак­торы, добиться полной аналогии построенной модели с натурой и т.д. Поэтому даже все­стороннее знание природы изучаемого процесса не гарантирует абсолютный успех.

При решении практических задач в гидравлике пользуются обеими известными ме­тодами построения моделей как физическим, так и математическим моделированием.

При физическом моделировании модель, как и натура, имеют одинаковую физиче­скую природу и отличаются друг от друга лишь размерами. При математическом модели­ровании модель имеет иное, чем натура, физическое содержание: общими у них являются лишь одинаковые дифференциальные уравнения, описывающие сходные физические про­цессы, протекающие в модели и натуре.

Подробное изучение методов моделирования не является задачей настоящего курса, эти вопросы рассматриваются в специальных дисциплинах. В настоящем курсе мы лишь назовём некоторые положения касающиеся основ построения таких моделей

14.1. Физическое моделирование

Физическая модель отличается от натуры лишь размерами, т.е. модель по своим раз­мерам может быть, чаще всего лишь уменьшенной копией натуры, либо она может (в не­которых случаях) превосходить по своим размерам натуру. И в том и другом случае, для успешного и правильного построения модели необходимо, прежде всего, знать основные законы подобия. Модель и натура будут адекватны между собой, если при построении модели будут выполнены все основные элементы подобия. К таким условиям относятся критерии геометрического, кинематического и динамического подобия.

Для геометрического подобия необходимо, чтобы отношение любых сопоставляе­мых линейных размеров модели и натуры были бы одинаковыми. Так протяжённость мо­дели и натуры, а также и другие прочие размеры должны находится между собой в про­порциональной зависимости:

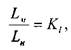
где:  и - линейный размер соответственно на модели и на натуре,

 - коэффициент геометрического подобия, масштаб моделирования.

В таком случае, при сопоставлении размеров площадей на модели и натуре должен соблюдаться такой же масштабный множитель, но с учётом порядка мерности величины:

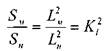
Т.е. при сопоставлении размеров площадей на модели и на натуре соотношение этих величин будет равно квадрату масштабного линейного множителя. Соответственно для сопоставления объёмов:

Для кинематического подобия необходимо, чтобы траектории всех сопоставимых частиц были геометрически подобны, т.е. при этом кроме геометрического подобия со­поставимых криволинейных отрезков модели и натуры выполнялось ещё подобие сопос­тавимых интервалов временни в моделе и натуре.

Тогда величины скоростей движения частиц в модели и натуре будут относиться между собой как:

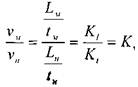 5 - величины расходов жидкости: '

Для динамического подобия сравниваемых потоков необходимо, чтобы в соответст­вующих местах потоков были подобны действующие в них одноимённые силы. Пусть в сопоставимых точках потока жидкости и строящейся модели этого потока действует неко­торая инерциальная сила F. Тогда при соблюдении геометрического и кинематического подобия, критерий динамического подобия может быть выражен следующим образом:

Величина носит название масштаба сил.

Рассмотрим критерии подобия отдельных сил действующих в жидкости.

Сила внутреннего трения в жидкости.

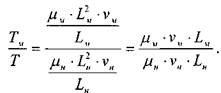
Заменив мы получим основное условие подобия потоков, в которых ос-

новную роль играют силы внутреннего трения жидкости. Для подобия таких потоков не­обходимо равенство чисел Рейнольдса.

Определяющей в потоке является сила тяжести.

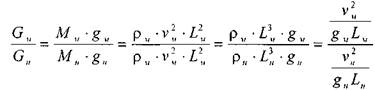 j

Таким образом, если определяющей силой в потоке является сила тяжести, то для подобия таких потоков необходимо постоянство числа Фруда

Для потока жидкости, в котором определяющей силой является сила давления:

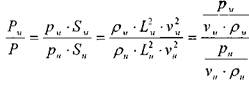
Если определяющей в потоке жидкости является сила давления, то для подобия та­ких потоков обязательным условием является равенство критерия Эйлера

14.2. Математическое моделирование

Для построения математических моделей в гидравлике могут быть использованы процессы, имеющие единую с гидравликой природу взаимодействия физических тел. Т.е. моделями для процессов, протекающих в жидкостях и газах, могут служить лишь те фи­зические процессы, которые относятся к группе электромагнитных взаимодействий, имеющих одного и того же переносчика взаимодействия - фотон. В таком случае основ­ные процессы, протекающие в модели и натуре, будут иметь одинаковые уравнения, опи­сывающие сходственные процессы.

Так для моделирования гидродинамического поля (поля скоростей движения жидко­сти и газа) могут быть использованы электрическое и тепловое поля.

Из курса физики известны общие уравнения, характеризующие сплошность поля и его изменение. Это известное уравнение неразрывности:

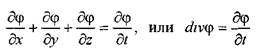
и так называемые уравнения неустановившегося (уравнение Фурье) и установивше­гося (уравнение Лапласа) движения:

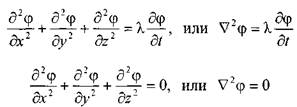
Наиболее удобным для целей моделирования процессов протекающих в жидкостях и газах являются процессы, протекающие в электрическом поле, поскольку последние отли­чаются компактностью, доступностью для измерения и, что самое главное, высокой ско­ростью протекания. Такие особенности электрического поля сделали его популярным для моделирования различных процессов, был разработан специальный аппарат для построе­ния электрических моделей процессов протекающих в жидкостях и газах, - метод электро­гидродинамической аналогии (ЭГДА). Построенные на его базе серийные моделирующие комплексы вплоть до появления цифровых ЭВМ широко использовались в практике на­учных исследований и на прямом производстве. При решении ряда задач актуальность этого метода остаётся поныне.

Модели, строящиеся на базе теплового поля, используются крайне редко из-за тру­доёмкости их создания и реализации.

Литература

1. Агроскин И.И, Дмитриев Г.Т., Пикалов Ф.И. Гидравлика. М., Госэнергоиздат, 1964

2. Альтшуль А.Д., Животовский Л.С., Иванов Л.П. Гидравлика и аэродинамика - М Строй-издат. 1987,4Юс.

3. Башта Т.М.,. Руднев С.С,. Некрасов Б.Б и др. Гидравлика, гидромашины и гидро­приводы.. «Машиностроение», 1982, 433с.

4. Гейер В.Г., Дулин B.C., Заря А.Н. Гидравлика и гидропривод. М.

5. Есьман И.Г. и др. Гидравлика и гидравлические машины. Баку, 1955

6. Некрасов Б.Б. Гидравлика и её применение в летательных аппаратах. М.Машиностроение, 1967. 368 с.

7. Орлов Ю.М. Механика жидкости, гидравлические машины и основы гидропривода. Учеб­ное пособие. Пермь, 2001. 379 с.

8. Рабинович Е.З. Гидравлика - М. «Недра» 1980,278 с.

9. Сборник задач по машиностроительной гидравлике: Учебное пособие для машино­строительных ВУЗов\ Д.А. Бугаев, З.А. Калмыкова, Л.Г. Подвидз и др. Под редак­цией И.И. Куколевского и Л.Г Подвидза.-4-е изд., перераб.-М: Машиностроение, 1981.-464 с. ил.

Похожие работы

Б.А. Бахметев дипломат, политик, мыслитель

Скачать

124283

0

0

... и никто в России не отдавал себе отчета и не имел ясного представления о том, как работает вообще мировая политическая мысль и каким образом вообще совершаются мировые события. Дипломатия, политика в лучшем случае рисовались как система известных навыков и приемов, присущих дипломатическим канцеляриям. Оценка дипломатического таланта и умения сводилась к признанию известной сноровки и ловкости в ...

Лекции по физике

Скачать

118786

4

0

праведливы соотношения ... Пусть высота тетраэдра равна ... . Тогда его объём равен ... . Воспользуемся вторым законом Ньютона и со- ставим уравнение движения тетраэдра: ... ... где ... - ускорение центра масс тетраэдра. Переходя к пределу (устремляя ... ), получим ... Получим формулу Коши, утверждающую, что напряжения на гранях образуют систему взаимно уравновешенных ...

Исследование работ Фарадея по электричеству

Скачать

166869

1

15

... самоиндукции и экстратоки замыкания и размыкания. Открытие явления электромагнитной индукции сразу же приобрело огромное научное и практическое значение; оно легло в основу электротехники. Работам Фарадея в области электричества положило начало исследование так называемых электромагнитных вращений. Из серии опытов Эрстеда, Араго, Био, Савара, проведенных в 1820 г., стало известно не только об ...

Инженерные системы

Скачать

120331

21

16

... фундамента. 59 Нормативный срок службы водозаборной арматуры, годы: А) 5; В) 10; С) 15; D) 20; E) 25. 60 Нормативный срок службы чугунных радиаторов, годы: А) 5; В) 10; С) 20; D) 30; E) 40. 61 Какой параметр ограничивается во всех инженерных системах? A) давление; B) скорость; C) температура; D) вязкость; E) расход. 62 Какая инженерная система рассчитывается для трех различных ...