Уравнение Бернулли для потока реальной жидкости

5.3. Уравнение Бернулли для потока реальной жидкости

При массовом расходе в живом сечении элементарной струйки . кинети-

ческая энергия жидкости проходящей через это сечение в единицу времени будет равна:

Суммируя величины кинетической энергии всех элементарных струек проходящих через живое сечение потока жидкости, найдём полную кинетическую энергию для всего

д

живого сечения потока

С другой стороны, полагая, что скорости во всех элементарных струйках одинаковы и равны средней скорости движения жидкости в живом сечении потока, таким же образом вычислим полную кинетическую энергию в этом же живом сечении потока. ' '

Вполне очевидно, что величины этих энергий не равны, т.е.

Тогда коэффициент, учитывающий неравномерность распределения скоростей по сечению (коэффициент Кориолиса) можно определить как соотношение кинетических энергий:

т?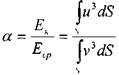

Внося эту поправку в уравнение для элементарной струйки жидкости, получим урав­нение для потока конечных размеров. Практически а= 1.0- 2,0.

Кроме коэффициента Кориолиса, учитывающего неравномерность распределения кинетической энергии по живому сечкнию потока, существует аналогичный показа­тель для величины количества движения, коэффициент Буссинэ

Секундное количество движения для потока жидкости можно определить как ин­тегральную сумму количества движения элементарных масс жидкости, протекающих через бесконечно малые площадки ds в пределах площади всего живого сечения S, т.е.

Аналогичным образом, величина количества движения жидкости в живом сече­нии при условии равномерного распределения сколостей по сечению потока будет:

Отсюда коэффициент Буссинэ определится следующим образом:

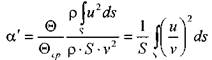
В связи с тем, что величина коэффициента количества движения (коэффициент Буссинэ) невелика и не превышает 1,05, поправкой в расчётах обычно пренебрегают,

5.4. Гидравлические сопротивления

Потери удельной энергии в потоке жидкости, безусловно, связаны с вязкостью жид­кости, но сама вязкость - не единственный фактор, определяющий потери напора. Но можно утверждать, что величина потерь напора почти всегда пропорциональны квадрату средней скорости движения жидкости. Эту гипотезу подтверждают результаты большин­ства опытных работ и специально поставленных экспериментов. По этой причине потери напора принято исчислять в долях от скоростного напора (удельной кинетической энергии потока). Тогда:

Потери напора принято подразделять на две категории:

потери напора, распределённые вдоль всего канала, по которому перемеща­ется жидкость (трубопровод, канал, русло реки и др.), эти потери пропорцио­нальны длине канала и называются потерями напора по длине сосредоточенные потери напора: потери напора на локальной длине потока (достаточно малой по сравнению с протяжённостью всего потока). Этот вид потерь во многом зависит от особенностей преобразования параметров пото­ка (скоростей, формы линий тока и др.). Как правило, видов таких потерь до­вольно много и их расположение по длине потока зачастую далеко не зако­номерно. Такие потери напора называют местными потерями или потерями напора на местных гидравлических сопротивлениях. Это вид потерь напора

также принято исчислять в долях от скоростного напора

Тогда полные потери напора можно представить собой как сумму всех видов потерь напора:

Оценка величины местных потерь напора практически всегда базируются на резуль­татах экспериментов, по результатам таких экспериментов определяются величины коэф­фициентов потерь. Для вычисления потерь напора по длине имеются более или менее на­дёжные теоретические предпосылки, позволяющие вычислять потери с помощью при­вычных формул.

5.5. Потери напора на местных гидравлических сопротивлениях Несмотря на многообразие видов местных гидравлических сопротивлений, их всё же можно при желании сгруппировать:

потери напора в руслах при изменении размеров живого сечения, потери напора на местных гидравлических сопротивлениях, связанных с из­менением направления движения жидкости, потери напора при обтекании преград.

Внезапное расширение русла. Внезапное расширение русла чаще всего наблюдается

на стыке участков трубопроводов, когда один трубопро­вод сочленяется с магистральным трубопроводом боль­шего диаметра. Величина коэффициента потерь напора в данном случае определяется с достаточной точностью на теоретическом уровне. Поток жидкости движущейся в трубопроводе меньшего диаметра d, попадая в трубу 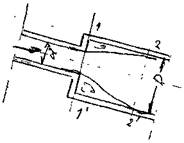 большего диаметра, касается стенок нового участка тру­бопровода не сразу, а лишь в сечении 2-2'. На участке между сечениями 1 - Г и 2-2' об­разуется зона, в которой жидкость практически не участвует в движении по трубам, обра­зуя локальный вихревой поток, где претерпевает деформацию. По этой причине часть ки­нетической энергии движущейся жидкости тратиться на поддержание «паразитного» сра­щения и деформации жидкости. Величины средних скоростей жидкости в сечениях можно определить из условия неразрывности.

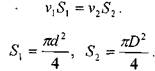
Тогда величина потерь напора при внезапном расширении русла определится:

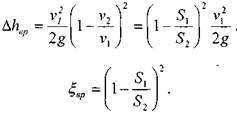
Таким образом, можно сказать, что потеря напора при внезапном расширении потока равна скоростному напору, соответствующему потерянной скорости.

Плавное расширение русла (диффузор). Плавное расширение русла называется диф­фузором. Течение жидкости в диффузоре име-

'ет сложный характер. Поскольку живое сече-

ние потока постепенно увеличивается, то, со­ответственно, снижается скорость движения  жидкости и увеличивается давление. Посколь­ку, в этом случае, в слоях жидкости у стенок

диффузора кинетическая энергия минимальна (мала скорость), то возможна остановка жидкости и интенсивное вихреобразование. По этой причине потери энергии напора в диффузоре будут зависеть от потерь напора на трение и за счёт потерь при расширении:

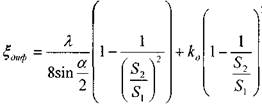 2

где: - площадь живого сечения на входе в диффузор,

S₂ - площадь живого сечения на выходе из диффузора, а - угол конусности диффузора,

 - поправочный коэффициент, зависящий от условий рас­ширения потока в диффузоре.

Внезапное сужение канала. При внезапном сужении канала поток жидкости отрыва­ется от стенок входного участка и лишь затем (в сечении 2 - 2)касается стенок канала

меньшего размера. В этой области потока — * образуются две зоны интенсивного вихре-образования (как в широком участке тру­бы, так и в узком), в результате чего, как и в предыдущем случае, потери напора скла­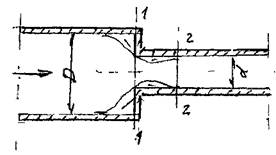 дываются из двух составляющих (потерь на трение и при сужении). Коэффициент

потерь напора при гидравлическом сопротивлении внезапного сужения потока можно оп­ределить по эмпирической зависимости, предложенной И.Е. Идельчиком:

или взять по таблице:

Плавноесужение канала. Плавное сужение канала достигается с помощью кониче­ского участка называемого конфузором. Потери напора в конфузоре образуются практи­чески за счёт трения, т.к. вихреобразование в конфузоре практически отсутствует. Коэф­фициент потерь напора в конфузоре можно определить по формуле:

, t f ~ *

При большом угле конусности а >50° коэффициент потерь напора можно определять по формуле с внесением поправочного коэффициента.

Нормальный вход в трубу. Из резервуаров, где хранятся жидкости вход в выкидной трубопровод осу­ществляется в так называемом нормальном исполне­нии, т.е. когда осевая линия патрубка трубопровода располагается по нормали к боковой стенку резервуара. Этот вид гидравлических сопротивлений также можно отнести к сопротивлениям связанным с изменением размеров русла, просто здесь размеры нового русла 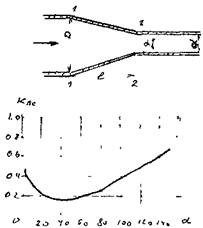 бесконечно малы по сравнению с размерами исходного русла с сечением резервуара. В этом случае внутри вы­кидного патрубка вытекающая из резервуара жидкость за­полняет всё сечение трубы не сразу, а лишь на некотором расстоянии от входа. В этой области в застойной зоне часть жидкости совершает вращательное движение и соз­данный таким образом вихрь порождает дополнительные г

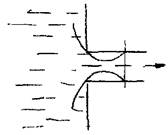 гидравлические сопротивления. Коэффициент потерь на­пора при этом приблизительно составляет половину ско­ростного напора:

Выход из трубы в покоящуюся жидкость. Это обычный эле­мент стыковки напорной части трубопровода с резервуаром. Вход­ной патрубок трубопровода располагается нормально к боковой 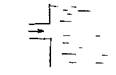 стенке резервуара. Этот вид гидравлических сопротивлений также можно рассматривать как разновидность внезапного расширения потока жидкости до бесконечно большого сечения. Вели­чина коэффициента потерь напора, в большинстве случаев, принимается равной одному скоростному напору.

Внезапный поворот канала. Под таким гидравличе­ским сопротивлением будем понимать место соединения 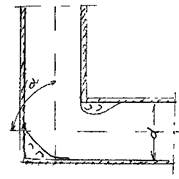 трубопроводов одинаковогодиаметра, при котором осевые линии трубопроводов не совпадают, т.е. составляют между

собой некоторый угол а Этот угол называется углом поворота русла, т.к. здесь изменяет­ся направление движения жидкости. Физические основы процесса преобразования кине­тической энергии при повороте потока достаточно сложны и следует рассмотреть лишь результат этих процессов. Так при прохождении участка внезапного поворота образуется сложная форма потока с двумя зонами вихревого движения жидкости На практике такие элементы соединения трубопроводов называют коленами. Следует отметить, что колено как соединительный элемент является крайне нежелательным ввиду значительных потерь напора в данном виде соединения. Величина коэффициента потерь напора будет, в первую очередь, зависеть от угла поворота русла и может быть определена по эмпирической фор­муле или по таблице:

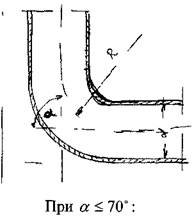
Плавный поворот канала Этот вид гидравлических сопротивлений можно считать более благоприятным (экономичным) с точки зрения величины потерь напора, т.к. в дан­ном случае опасных зон для образования интенсивного вихревого движения жидкости практически нет. Тем не менее, под действием того, что при повороте потока возникают центробежные силы, способствующие отрыву частиц жидкости от стенки трубы, вихре­вые зоны всё же возникают. Кроме того, при этом возникают встречные потоки жидкости

направленные от внутренней стенки трубы к внешней стенке трубы. Коэффициент потерь

напора определяется по эмпирическим формулам или по

таблицам. При угле поворота русла на 90° и:

При угле поворота русла а)100° :

  i

при а = 90°

Здесь: R - радиус закругления трубы, г - радиус трубы.

Если, то данные таблицы следует умножать на коэффициент:

Кроме приведённых зависимостей имеются и другие справочные сведения. Наличие обширного набора сведений по этим вопросам объясняется тем, что колена в закруглён­ном исполнении весьма широко применяются в строительстве трубопроводов и в различ­ных гидравлических системах.

Задвижки. Задвижки часто используют как средст­во регулирования характеристик потока жидкости (рас­ход, напор, скорость). При наличии задвижки в трубо­проводе поток обтекает находящиеся в трубе плашки 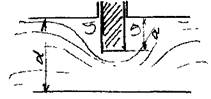 задвижки, наличие которых ограничивает живое сечение потока, а также приводит к возникновению вихревых

потоков жидкости около плашек задвижки. Коэффициент потерь напора зависит от степе­ни закрытия задвижки

Краны. Краны также могут использоваться в качестве средств регулирования пара­метров потока. В этих случаях коэффициент потерь напора зависит от степени закрытия крана (угла поворота).

Обратные клапаны и фильтры. Коэффициенты потерь напора определяются, как пра­вило, экспериментально.

Похожие работы

Б.А. Бахметев дипломат, политик, мыслитель

Скачать

124283

0

0

... и никто в России не отдавал себе отчета и не имел ясного представления о том, как работает вообще мировая политическая мысль и каким образом вообще совершаются мировые события. Дипломатия, политика в лучшем случае рисовались как система известных навыков и приемов, присущих дипломатическим канцеляриям. Оценка дипломатического таланта и умения сводилась к признанию известной сноровки и ловкости в ...

Лекции по физике

Скачать

118786

4

0

праведливы соотношения ... Пусть высота тетраэдра равна ... . Тогда его объём равен ... . Воспользуемся вторым законом Ньютона и со- ставим уравнение движения тетраэдра: ... ... где ... - ускорение центра масс тетраэдра. Переходя к пределу (устремляя ... ), получим ... Получим формулу Коши, утверждающую, что напряжения на гранях образуют систему взаимно уравновешенных ...

Исследование работ Фарадея по электричеству

Скачать

166869

1

15

... самоиндукции и экстратоки замыкания и размыкания. Открытие явления электромагнитной индукции сразу же приобрело огромное научное и практическое значение; оно легло в основу электротехники. Работам Фарадея в области электричества положило начало исследование так называемых электромагнитных вращений. Из серии опытов Эрстеда, Араго, Био, Савара, проведенных в 1820 г., стало известно не только об ...

Инженерные системы

Скачать

120331

21

16

... фундамента. 59 Нормативный срок службы водозаборной арматуры, годы: А) 5; В) 10; С) 15; D) 20; E) 25. 60 Нормативный срок службы чугунных радиаторов, годы: А) 5; В) 10; С) 20; D) 30; E) 40. 61 Какой параметр ограничивается во всех инженерных системах? A) давление; B) скорость; C) температура; D) вязкость; E) расход. 62 Какая инженерная система рассчитывается для трех различных ...