Навигация
Дифференциальное уравнение равновесия жидкости
2.4. Дифференциальное уравнение равновесия жидкости
После рассмотрения некоторых частных случаев равновесия жидкости рассмотрим общее диф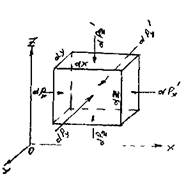 ференциальное равновесия в самом общем виде. Для этой цели выделим отсек жидкости малых размеров в виде параллелепипеда. Масса жидкости в выделенном объёме:
ференциальное равновесия в самом общем виде. Для этой цели выделим отсек жидкости малых размеров в виде параллелепипеда. Масса жидкости в выделенном объёме:
![]()
На боковые грани параллелепипеда действуют силы давления: (на левую и правую грани соответственно):![]() . На переднюю и заднюю грани:
. На переднюю и заднюю грани: ![]() , на нижнюю
, на нижнюю
и верхнюю грани:![]()
![]()
Поскольку давление на правую грань больше, то i![]()
По аналогии можно записать силы давления на остальные пары граней.
на переднюю ![]() , на заднюю
, на заднюю ![]() , на нижнюю
, на нижнюю
![]() , на верхнюю
, на верхнюю![]() Проекции массовых сил на координатные оси:
Проекции массовых сил на координатные оси:
на ось ОХ будет на ось ОУ будет
на ось OZ будет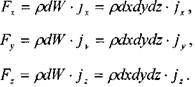 Тогда сумма сил действующих вдоль оси ОХ:
Тогда сумма сил действующих вдоль оси ОХ:
![]()
сумма сил действующих вдоль оси 07:
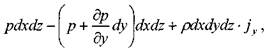
сумма сил действующих вдоль оси OZ:
![]()
где:![]() , проекции ускорения массовых сил на координатные оси.
, проекции ускорения массовых сил на координатные оси.
После преобразования получим систему дифференциальных уравнений равновесия жидкости:
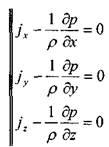 i i >
i i >
2.5. Сообщающиеся сосуды
В своей практической деятельности человек часто сталкивается с вопросами равновесия жидкости в сообщающихся сосудах, когда два сосуда А и В соединены между собой жёстко или гибким шлангом. Сами сосуды (А и В) обычно называются коленами. Такой гидравлический элемент часто используется в различных гидравлических машинах (гидравлические прессы и др.), системах гидропривода и гидроавтоматики, различных измерительных приборах и в ряде других случаев. С природ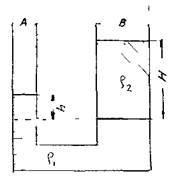 ными сообщающимися сосудами человек встречается с давних пор: сообщающимися сосудами больших размеров являются водонасыщенные пласты горных пород с системой колодцев, играющих роль отдельных колен природной гидродинамической системы.
ными сообщающимися сосудами человек встречается с давних пор: сообщающимися сосудами больших размеров являются водонасыщенные пласты горных пород с системой колодцев, играющих роль отдельных колен природной гидродинамической системы.
В открытых сообщающихся сосудах, заполненных однородной жидкостью свободный уровень жидкости устанавливается на одном и том же уровне в обоих коленах. Если в коленах сосудов залиты две несмешивающиеся жидкости с различной плотностью, то свободные уровни жидкости в правом и левом коленах устанавливаются на разных высотах в зависимости от соотношения плотностей жидкостей.
Для типичного случая, изображённого на рисунке, запишем уравнение равновесия жидкости относительно уровня раздела жидкостей.
или: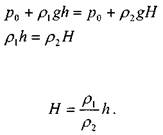
В закрытых сообщающихся сосудах давления на свободную поверхность могут быть шными, тогда уравнение равновесия будет иметь следующий вид:
![]()
2.6. Сила давления жидкости па плоскую поверхность, погружённую в жидкость
Согласно основному закону гидростатики величина давления р определяется глубиной погружения точки под уровень свободной поверхности h жидкости и величиной
плотности жидкости р.
Для горизонтальной поверхности величина давления одинакова во всех точках этой поверхности, т.к.:
 Отсюда:
Отсюда:![]()
![]()
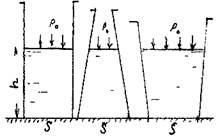
Таким образом, Сила давления жидкости на горизонтальную поверхность (дно сосуда) равно произведению площади этой поверхности на величину давления на глубине погружения этой поверхности. На рисунке показан так называемый «гидравлический парадокс», здесь величины силы давления на дно всех сосудов одинаковы, независимо от формы стенок сосудов и их физической высоты, т.к. площади доньев у всех сосудов одинаковы, одинаковы и величины давлений.
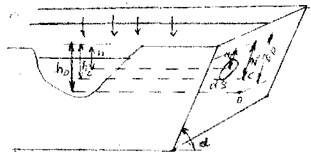
Сила давления на наклонную поверхность, погруженную в жидкость. Практическим примером такой поверхности может служить наклонная стенка сосуда. Для вывода урав-
нения и вычисления силы давления на стенку выберем следующую систему координат: ось ОХ направим вдоль пересечения плоскости свободной поверхности жидкости с наклонной стенкой, а ось OZ направим вдоль этой стенки перпендикулярно оси ОХ. Тогда в качестве координатной плоскости XOZ будет выступать сама наклонная стенка. На плоскости стенки выделим малую площадку![]() , которую, в связи с малыми размерами можем считать горизонтальной. Величина давления на глубине площадки будет равна:
, которую, в связи с малыми размерами можем считать горизонтальной. Величина давления на глубине площадки будет равна:
![]()
где: h - глубина погружения площадки относительно свободной поверхности жидкости (по вертикали).
 Сила
Сила![]() давления
давления![]() dP на площадку:
dP на площадку:
Для определения силы давления
на всю смоченную часть наклонной стенки (часть площади стенки сосуда, расположенная ниже уровня свободной поверхности жидкости) необходимо проинтегрировать это уравнение по всей смоченной части площади стенки S .
![]()
Интеграл![]() представляет собой статический момент площади S относительно
представляет собой статический момент площади S относительно
оси ОХ. Он, как известно, равен произведению этой площади на координату её центра тяжести zc. Тогда окончательно:
![]()
Таким образом, сила давления на наклонную плоскую поверхность, погружённую в жидкость равна смоченной площади этой поверхности на величину давления в центре тяжести этой площади. Сила давления на плоскую стенку кроме величины и направления характеризуется также и точкой приложения этой силы, которая называется центром давления.
Центр давления силы атмосферного давления p0S будет находиться в центре тяжести площадки, поскольку атмосферное давление передаётся на все точки жидкости одинаково. Центр давления самой жидкости на площадку можно определить исходя из теоремы о моменте равнодействующей силы. Согласно этой теореме момент равнодействующей
силы относительно оси ОХ будет равен сумме моментов составляющих сил относительно этой же оси.
![]()
откуда: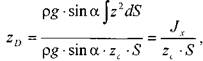
где:- положение центра избыточного давления на вертикальной оси,
![]() - момент инерции площадки S относительно оси ОХ.
- момент инерции площадки S относительно оси ОХ.
Отсюда центр давления (точка приложения равнодействующей силы избыточного давления) расположен всегда ниже центра тяжести площадки. В сучаях, когда внешнней действующей силой на свободную поверхность жидкости является сила атмосферного давления, то на стенку сосуда будут одновременно действовать две одинаковые по величине и противоположные по направлению силы обусловленные атмосферным давлением (на внутреннюю и внешнюю стороны стенки). По этой причине реальной действующей несбалансированной силой остаётся сила избыточного давления.
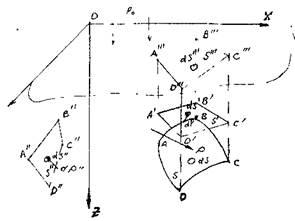
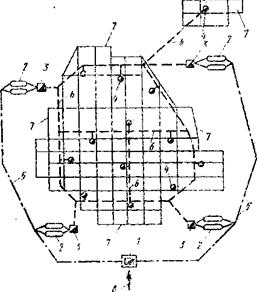
2.7. Сила давления на криволинейную поверхность, погружённую в жидкость Выберем внутри покоящейся жидкости криволинейную поверхность ABCD, которая может быть частью поверхности некоторого тела погруженного в жидкость. Построим проекции этой поверхности на координатные плоскости. Тогда в координатной плоскости XOZ проекцией этой поверхности будет плоская поверхность ![]() , в координатной
, в координатной
плоскости YOZ — плоская поверхность![]() и в плоскости свободной поверхности
и в плоскости свободной поверхности
жидкости (координатная плоскость ХОТ) - плоская поверхность ![]() . На криволи-
. На криволи-
нейной поверхности выделим малую площадку dS, проекции которой на координатные
плоскости будут соответственно ![]() . Сила давления на криволинейную поверхность dP будет направлена по внутренней нормали к этой поверхности и может быть представлена в виде:
. Сила давления на криволинейную поверхность dP будет направлена по внутренней нормали к этой поверхности и может быть представлена в виде:
Горизонтальные составляющие могут быть определены, как силы давления
' ' -
на проекции
' -
на проекции![]() малой площадки dS на соот-
малой площадки dS на соот-
ветствующие координатные плоскости:
![]()
![]()
Интегрируя эти уравнения, получим (как в случае с давлением на наклонную поверхность):
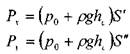
Вертикальная составляющая силы давления:
^![]()
Второй интеграл в этом равенстве представляет собой объём образованный рассматриваемой криволинейной поверхностью ABCD и её проекцией на свободную поверхность жидкости![]() . Этот объём принято называть телом давления
. Этот объём принято называть телом давления![]()
![]()
Таким образом, горизонтальные составляющие силы давления на криволинейную поверхность равны давлениям на вертикальные проекции этой поверхности, а вертикальная составляющая равна весу тела давления, и силе внешнего давления на горизонтальную проекцию криволинейной поверхности.
Основные уравнения гидростатики широко используются на практике. Примероми могут служить простейшие гидравлические машины - гидравлический пресс, построенный по принципу сообщающихся сосудов и гидравлический аккумулятор.
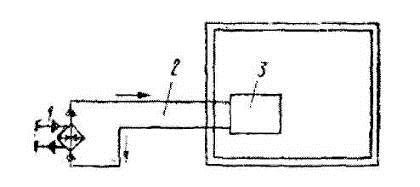
Гидравлический пресс состоит из двух цилиндров приводного (1) и рабочего (2) со-
единеных между собой трубопроводом и представляет систему сообщающихся сосудов. В приводном цилиндре перемещается плунжер малого диаметра d, в рабочем цилиндре находится поршень с большим диаметром D. Связь между плунжером и рабочим поршнем осуществ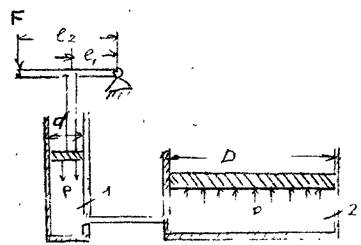 ляется через рабочую жидкость, заполняющую гидравлическую систему (сообщающиеся сосуды). Усилие F через рычаг передаются рабочей жидкости.
ляется через рабочую жидкость, заполняющую гидравлическую систему (сообщающиеся сосуды). Усилие F через рычаг передаются рабочей жидкости.
Сила давления на жидкость под плунжером Р] передаёт жидкости давление р, которое, в свою очередь, передаётся во все точки рабочего поршня.
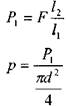
Тогда сила давления на поверхность рабочего поршеня будет равна'
![]()
Таким образом, с помощью гидравлического пресса, приложенная к концу рычага
^ сила, увеличивается в![]() раз.
раз.
Похожие работы
... и никто в России не отдавал себе отчета и не имел ясного представления о том, как работает вообще мировая политическая мысль и каким образом вообще совершаются мировые события. Дипломатия, политика в лучшем случае рисовались как система известных навыков и приемов, присущих дипломатическим канцеляриям. Оценка дипломатического таланта и умения сводилась к признанию известной сноровки и ловкости в ...
праведливы соотношения ... Пусть высота тетраэдра равна ... . Тогда его объём равен ... . Воспользуемся вторым законом Ньютона и со- ставим уравнение движения тетраэдра: ... ... где ... - ускорение центра масс тетраэдра. Переходя к пределу (устремляя ... ), получим ... Получим формулу Коши, утверждающую, что напряжения на гранях образуют систему взаимно уравновешенных ...
... самоиндукции и экстратоки замыкания и размыкания. Открытие явления электромагнитной индукции сразу же приобрело огромное научное и практическое значение; оно легло в основу электротехники. Работам Фарадея в области электричества положило начало исследование так называемых электромагнитных вращений. Из серии опытов Эрстеда, Араго, Био, Савара, проведенных в 1820 г., стало известно не только об ...
... фундамента. 59 Нормативный срок службы водозаборной арматуры, годы: А) 5; В) 10; С) 15; D) 20; E) 25. 60 Нормативный срок службы чугунных радиаторов, годы: А) 5; В) 10; С) 20; D) 30; E) 40. 61 Какой параметр ограничивается во всех инженерных системах? A) давление; B) скорость; C) температура; D) вязкость; E) расход. 62 Какая инженерная система рассчитывается для трех различных ...

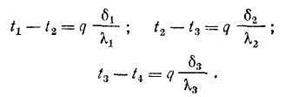
0 комментариев