Конечномерные представления

2.4. Конечномерные представления.

Теорема 2.7. Пусть π – конечномерное представление *-алгебры А. Тогда π = π1…..πn , где πi неприводимы.

Доказательство. Если dimπ = 0 (n=0), то все доказано. Предположим, что dimπ = q и что наше предложение доказано при dimπ<q. Если π неприводимо, то предложение снова доказано. В противном случае π = π΄  π΄΄, причем dimπ΄<q, dimπ΄΄<q, и достаточно применить предположение индукции.

Разложение π = π1…..πn не единственно. Тем не менее, мы получим некоторую теорему единственности.

Пусть ρ1, ρ2 – два неприводимых подпредставления π. Им отвечают инвариантные подпространства Н1 и Н2. Пусть Р1 и Р2 – проекторы Н на Н1 и Н2. Они коммутируют с π(А). Поэтому ограничение Р2 на Н1 есть оператор, сплетающий ρ1 и ρ2. Следовательно, если Н1 и Н2 не ортогональны, то из пункта 2.3. следует, что ρ1 и ρ2 эквивалентны. Это доказывает, что любое неприводимое подпредставление π эквивалентно одному из πi . Итак, перегруп- пировав πi , получаем, что π = ν1…..νm, где каждое νi есть кратное ρiνi΄ неприводимого представления νi΄, и νi΄ попарно эквивалентны. Если ρ – неприводимое представление π, то предыдущее рассуждение показывает, что соответствующее инвариантное подпространство Н΄ ортогонально всем инвариантным подпространствам Нi, отвечающих νi, кроме одного. Поэтому Н΄ содержится в одном из Нi. Это доказывает, что каждое пространство Нi определяется однозначно: Нi – это подпространство Н, порожденное пространствами подпредставлений π, эквивалентных νi΄. Таким образом, доказано предложение.

Теорема 2.8. В разложении π = ρ1ν1΄…..ρmνm΄ представления π, (где ν1΄,…, νm΄ неприводимы и неэквивалентны) целые числа ρi и классы представлений νi΄ определяются единственным образом, как и пространства представлений.

2.5. Интегрирование и дезинтегрирование представлений. Напомним определение борелевского пространства.

Определение 2.7. Борелевским пространством называется множество Т, снабженное множеством В подмножеств Т, обладающим следующими свойствами: ТВ, ØВ, В инвариантно относительно счетного объединения, счетного пересечения и перехода к дополнению.

Определение 2.8. Пусть Т1, Т2 – борелевские пространства. Отображение f: Т1→Т2 называется борелевским, если полный прообраз относительно f любого множества в Т2 есть борелевское множество в Т1.

Дадим несколько вспомогательных определений и утверждений.

Пусть Т – борелевское пространство и μ – положительная мера на Т.

Определение 2.9. μ – измеримое поле гильбертовых пространств на Т есть пара ε = ((H(t))tT, Г), где (H(t))tT – семейство гильбертовых пространств, индексы которых пробегают Т, а Г – множество векторных полей, удовлетворяющее следующим условиям:

(i) Г – векторное подпространство Н(t);

существует последовательность (х1, х2,…) элементов Г таких, что для любого tT элементы хn(t) образуют последовательность H(t);

для любого хГ функция t→||x(t)|| μ – измерима;

пусть х – векторное поле; если для любого yГ функция t→(x(t), y(t)) μ – измерима, то хГ.

Пусть ε = ((H(t))tT, Г) μ – измеримое поле гильбертовых пространств на Т. Векторное поле х называется полем с интегрируемым квадратом, если хГ и ||x(t)||2 dμ(t) < +∞.

Если х, y – с интегрируемым квадратом, то х+y и λх (λС) – тоже и функция t →(x(t), y(t)) интегрируема; положим

(x, y) = (x(t), y(t)) dμ(t)

Тогда векторные поля с интегрируемым квадратом образуют гильбертово пространство Н, называемое прямым интегралом Н(t) и обозначаемое x(t)dμ(t).

Определение 2.10. Пусть ε = ((H(t))tT, Г) – измеримое поле гильбер- товых пространств на Т. Пусть для любого tT определен оператор S(t)L(H(t)). Если для любого хT поле t→S(t)x(t) измеримо, то t→S(t) называется измеримым операторным полем.

Пусть Т – борелевское пространство, μ - положительная мера на Т, t→Н(t) - μ - измеримое поле гильбертовых пространств на Т. Пусть для каждого tT задано представление π(t) *-алгебры А в Н(t): говорят, что t→π(t) есть поле представлений А.

Определение 2.11. Поле представлений t→π(t) называется измеримым, если для каждого хА поле операторов t→π(t)х измеримо.

Если поле представлений t→π(t) измеримо, то для каждого хА можно образовать непрерывный оператор π(х)=π(t) (x) dμ(t) в гильбертовом прост- ранстве Н =Н(t) dμ(t).

Теорема 2.9. Отображение х→π(х) есть представление А в Н.

Доказательство. Для любых х, yА имеем

π(х+y) = π(t) (x+y) dμ(t) = (π(t) (x) + π(t) (y)) dμ(t) =π(t) (x )dμ(t) +

+π(t) (y) dμ(t) = π(х) +π(y)

Аналогично π(λх) = λπ(х), π(хy) = π(х) π(y), π(х*)=π(х)*

Определение 2.12. В предыдущих обозначениях π называется прямым интегралом π(t) и обозначается π =π(t) dμ(t).

Определение 2.13. Операторное поле t→φ(t)I(t)L(H(t)) где I(t)-единичный оператор в H(t), называется диагональным оператором в Н=Н(t)dμ(t).

Пусть ε = ((H(t))tT, Г) – μ-измеримое поле гильбертовых пространств на Т, μ1 – мера на Т, эквивалентная μ (то есть каждая из мер μ1, μ абсолютно непрерывна по другой), и ρ(t)=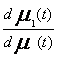. Тогда отображение, которое каждому хН==Н(t)dμ(t) составляет поле t→ρ(t)-1/2х(t)Н1=Н(t) dμ1(t),

есть изометрический изоморфизм Н на Н1, называемый каноническим.

Действительно,

||ρ(t)-1/2х(t)dμ1(t)||2 = ||х(t)||2ρ(t)-1 dμ1(t) = ||х(t)||2dμ1(t) = ||х(t)||2

Теорема 2.10. Пусть Т – борелевское пространство, μ – мера на Т, t→Н(t) – измеримое поле гильбертовых пространств на Т, t→π(t) – измеримое поле представлений А в Н(t),

Н =Н(t) dμ(t) , π1==π(t )dμ(t),

Д – алгебра диагональных операторов в Н. Пусть μ1 – мера на Т, эквивалентная μ,

Н1 =Н(t) dμ1(t) , π1 =π(t) dμ1(t),

Д1 – алгебра диагональных операторов в Н1. Тогда канонический изоморфизм преобразует π в π1 и Д в Д1.

Доказательство. Пусть ρ(t)=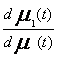. Канонический изоморфизм из Н в Н1 есть изометрический изоморфизм, который переводит х =x(t) dμ(t)Н в

Ux = ρ-1/2х(t) dμ1(t).

Пусть α А. Имеем

π1(α)Ux = π(t)(α) ρ-1/2 х(t) dμ1(t) = Uπ(t)(α) х(t) dμ(t) = Uπ(α)x,

поэтому и преобразуем π в π1. Тогда если SД, то аналогично SUx = USx, для любого хН.

Определение 2.14. Пусть Т, Т1 – борелевские пространства; μ, μ1 – меры на Т и Т1 соответственно; ε = ((H(t))tT, Г), Z1 = ((H1(t1))t1T1, Г), - μ-измеримое и μ1-измеримое поля гильбертовых пространств. Пусть η: Т→Т1 – борелевский изоморфизм, переводящий μ в μ1; η-изоморфизм ε на ε1 называется семейство (V(t))tT, обладающее следующими свойствами:

для любого tT отображение V(t) является изоморфизмом Н(t) на Н1(η(t));

для того, чтобы поле векторов t→x(t)H(t) на Т было μ-измеримо, необходимо и достаточно, чтобы поле η(t)→V(t)х(t) Н1(η(t)) на Т1 было μ1-измеримо.

Отображение, переводящее поле хН =Н(t) dμ(t) в поле η(t))→V(t)х(t) Н1 = Н1(t) dμ1(t) , есть изоморфизм Н на Н1, обозначаемый V(t) dμ(t).

Теорема 2.11. Пусть Т – борелевское пространство; μ – мера на Т, t→H(t) – μ- измеримое поле гильбертовых пространств на Т, t→ π(t) - μ- измеримое поле представлений А в H(t),

Н =Н(t) dμ(t), π ==π(t) dμ(t),

Д – алгебра диагональных операторов в Н. Определим аналогичным образом Т1, μ1, t1→H1(t1), t1→ π1(t1), Н1, π1, Д1.

Предположим, что существует:

N, N1 – борелевские подмножества Т и Т1, такие что μ (N) = μ (N1) = 0;

борелевский изоморфизм η: TN →TN1, преобразует μ в μ1;

η-изоморфизм t→V(t) поля t→Н(t) (tZN) на поле t1→Н1(t1) (t1Т1N1) такой, что V(t) преобразует π(t) в π1(η(t)) для каждого t.

Тогда V =V(t)dμ(t) преобразует Д в Д1 и π в π1.

Доказательство. Обозначим через It, It1 единичные операторы в Н(t) и Н1(t1). Если fL∞(T, μ) и если f1 – функция на Т1N1, получаемая из f|(TN) при помощи η, то V преобразует f(t)It dμ(t) в f1(t1) It1 dμ1(t1), поэтому V преоб- разует Д в Д1. С другой стороны, пусть αА и х = х(t) dμ(t)Н.

Тогда

Vπ(α)х = Vπ(t)(α) х(t) dμ(t) = V(η-1(t1)) π(η-1(t1))(α) х(η-1(t1)) dμ1(t1) = π1(t1)(α) V(η-1(t1)) х(η-1(t1)) dμ1(t1) = π1 (α) V х

Поэтому V преобразует π в π1.

Приведем примеры прямых интегралов.

Пусть имеется последовательность гильбертовых пространств  и дискретная мера μ на N, то есть μ(n)=1 для любого nN. Тогда

Н(n) dμ(n) = Н(n), то есть прямой интеграл сводится к ортогональ- ной сумме.

Пусть Т=[0, 1] и в каждой точке tТ соответствует поле комплексных чисел С, и на Т задана линейная мера Лебега dt. Тогда С dt = L2 (0, 1).

Изоморфизм устанавливается отображением х = х(t) dt →х(t)L2 (0, 1).

Разложения представления на неприводимые представления в прямой интеграл называют дезинтегрированием.

§ 3. Тензорные произведения пространств

3.1. Тензорные произведения пространств. Пусть  - конечная последовательность сепарабельных гильбертовых пространств,  - некоторый ортонормированный базис в Нк.

Образуем формальное произведение

 (3.1.)

α = (α1,…, αn)  (n раз), то есть рассмотрим упорядо- ченную последовательность ( ) и на формальные векторы (3.1.) натянем гильбертово пространство, считая, что они образуют его ортонормиро- ванный базис. Полученное сепарабельное гильбертово пространство называется тензорным произведением пространств Н1,…, Нn и обозначается Н1,…, Нn = . Его векторы имеют вид:

f =  (fαC), || f ||2 =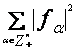< ∞ (3.2.)

Пусть g = , тогда скалярное произведение опреде- ляется формулой

(f, g) =  (3.3.)

Пусть f(k) = (к = 1,…, n) – некоторые векторы. По определению

f = f(1)… f(n) =  (3.4.)

Коэффициенты fα =  разложения (3.4.) удовлетворяют условию (3.2.), поэтому вектор (3.4.) принадлежит , при этом

|| f || =  (3.5.)

Функция Н1,…, Нn <>   линейна по каждому фрагменту, а линейная оболочка L векторов (3.4.) плотна в  - эта линейная оболочка называется алгебраическим (непополненным) тензорным произведением пространств Н1,…, Нn и обозначается α.

Приведенное определение тензорного произведения зависит от выбора ортогонального базиса в каждом сомножителе . При изменении базисов получаем тензорное произведение, изоморфное с сохранением своей структуры исходному произведению.

Пусть Н1 и Н2 – гильбертовы сепарабельные пространства. Тогда конструкция тензорного произведения означает следующее. Рассматривается линейная оболочка L формальных произведений f1 f2, причем считается, что

(f1 + g1) f2 = f1 f2 + g1 f2 (3.6.)

f1 (f2 + g2) = f1 f2 + f1 g2 (3.7.)

(λ f1) f2=λ (f1 f2) (3.8.)

f1 λ (f2) = λ (f1 f2) (3.9.)

f1, g1Н1; f2, g2 Н2; λ С.

Иными словами, линейное пространство L факторизируется по его линейному подмножеству, натянутому на всевозможные векторы, имеющие вид разностей между правыми и левыми частями равенств (3.6.) – (3.9.).

Затем вводится скалярное произведение в L.

(f1 f2 , g1 g2 ) = (f1 g1)(f2 g2) (3.10.)

f1, g1Н1; f2, g2 Н2,

а затем распространяется на другие элементы из факторизованного L билинейным образом.

Похожие работы

*-Алгебры и их применение

Скачать

69018

1

0

... ;0,0(p2) = P0,0. В силу теоремы 2.8. главы I разложения I, Р1 и Р2 также определяются однозначно. § 2. Два ортопроектора в сепарабельном гильбертовом пространстве 2.1. Неприводимые *-представления *-алгебры P2 . Пусть А = Р1 - Р1┴ = 2Р1 – I и В = Р2 – Р2┴ = 2Р2 – I. Тогда А2 = I , В2 = I. Следовательно А и В самосопряженные унитарные операторы в Н. Положим U=АВ, тогда U-1=ВА и А-1UА ...

Изучение элементов современной алгебры, на примере подгрупп симметрических групп, на факультативных занятиях по математике

Скачать

75806

4

238

... для того, чтобы показать школьникам образец современной математической теории. 2.2.3.2. ПРОГРАММА И СОДЕРЖАНИЕ ЗАНЯТИЙ ФАКУЛЬТАТИВНОГО КУРСА «ЭЛЕМЕНТЫ СОВРЕМЕННОЙ АЛГЕБРЫ» В качестве экспериментальной работы мы предлагаем изучение элементов современной алгебры в рамках факультативного курса по математике. Нами была разработана программа факультативного курса «Элементы современной алгебры» и ...

Алгебра логики

Скачать

10756

9

3

... угодно сложные в логическом отношении схемы, можно строить, используя два приема: 1.  последовательное соединение элементов; 2.  перестановка входов элементов. Этим двум физическим приемам в алгебре логики соответствуют: 1.  принцип суперпозиции (подстановка в функцию вместо ее аргументов других функций); 2.  подстановка аргументов (изменение порядка записи аргументов функций или замена ...

Вопросы к гос. экзамену по дисциплине "Математика – Алгебра"

Скачать

66655

0

0

... 4. Бинарные отношения. Математика как наука отражает мир взаимодействующих простых и сложных объектов (вещей, явлений, процессов). Абстрагируясь от реальности, математика рассматривает унарные, бинарные и другие отношения. В вопросе требуется рассмотреть бинарные отношения, их свойства и особо обратить внимание на отношение эквивалентности, заданного на одном множестве. Рассмотрим ...